摘 要: 支持向量機(jī)(SVM)是一種兩類分類算法,如何將SVM算法應(yīng)用于多類分類問題,目前已衍生出多種方法。其中“二叉樹”方法應(yīng)用比較廣泛,但分類支持向量機(jī)在樹中中間節(jié)點(diǎn)位置的不同,直接關(guān)系到該方法的分類準(zhǔn)確性。基于二叉樹方法提出了“類間相異度”的策略,根據(jù)類間相異程度來決定多類的分類順序。
關(guān)鍵詞: 支持向量機(jī);二叉樹;超球體;相異度
支持向量機(jī)SVM(Support Vector Machine)[1]是一種基于統(tǒng)計(jì)學(xué)的VC維理論[2]和結(jié)構(gòu)風(fēng)險(xiǎn)最小化原理基礎(chǔ)之上的兩類分類算法。目前,該算法已廣泛應(yīng)用于諸多領(lǐng)域,如人臉檢驗(yàn)、文字/手寫體識(shí)別、圖像處理[3]等。支持向量機(jī)屬于一種機(jī)器學(xué)習(xí)算法,核函數(shù)則是其中的核心部分。對于難以分類的低維空間向量集,通常的做法是向高維空間集轉(zhuǎn)化,但這也增加了計(jì)算的復(fù)雜度,即維數(shù)災(zāi)難[4]問題。而核函數(shù)[4]卻可以很好地解決這個(gè)問題,只要選取合適的核函數(shù),即可得到高維空間的向量機(jī)(也稱超平面[2])。
當(dāng)使用向量機(jī)進(jìn)行多類分類時(shí),需要將多類問題轉(zhuǎn)化為兩類問題。常用的有“一對多”(One Versus Rest)[5]、“一對一”(One Versus One)[6]、“二叉樹”(Binary Tree)[7]和“有向無環(huán)圖”(Directed Acyclic Graph)[8]等方法,本文將對多類分類支持向量機(jī)[9]的這些方法作概略介紹和比較,同時(shí)對基于偏二叉樹多類分類向量機(jī)提出一些改進(jìn)意見。
1 SVM多類分類方法
1.1 SVM多類分類方法介紹
現(xiàn)有一個(gè)多類分類問題,其中類別數(shù)為k。當(dāng)使用支持向量機(jī)對此問題進(jìn)行分類時(shí),需假設(shè)一類為正樣本,另一類為負(fù)樣本。
“一對多”方法將類i樣本作為正樣本,而除該類以外的所有類作為負(fù)樣本,在這兩類樣本間訓(xùn)練出向量機(jī),該方法總共構(gòu)造了k個(gè)分類支持向量機(jī)。在對某向量進(jìn)行測試時(shí),取計(jì)算出最大值的向量機(jī)所對應(yīng)的類別作為該向量的類別。
“一對一”方法是從分類問題中選取類別i和類別j中的樣本數(shù)據(jù)訓(xùn)練兩類間的分類向量機(jī),這樣構(gòu)造出的向量機(jī)的總數(shù)為k(k-1)/2。雖然“一對一”分類方法產(chǎn)生的分類向量機(jī)的數(shù)目是“一對多”方法的(k-1)/2倍,但“一對一”方法的訓(xùn)練規(guī)模要比“一對多”方法小很多。對向量的測試采取計(jì)分的方式,通過k(k-1)/2個(gè)分類機(jī)的計(jì)算以后,選取得分最高的類別作為該測試數(shù)據(jù)的類別。
二叉樹方法是將兩類之間的k-1個(gè)向量機(jī)作為中間節(jié)點(diǎn),葉子節(jié)點(diǎn)對應(yīng)k個(gè)類別樣本,以這樣的方式構(gòu)建一棵分類二叉樹,常用的方式包括滿二叉樹和偏二叉樹。在對樣本進(jìn)行訓(xùn)練時(shí),根節(jié)點(diǎn)的向量機(jī)在全部樣本空間上進(jìn)行訓(xùn)練,而子節(jié)點(diǎn)向量機(jī)則在根節(jié)點(diǎn)的負(fù)樣本類或正樣本類上訓(xùn)練,依次類推,直至k-1個(gè)分類機(jī)在k-1類和k類樣本上進(jìn)行訓(xùn)練。
有向無環(huán)圖方法與“一對一”方法一樣,也是在任意兩類之間訓(xùn)練分類向量機(jī),也即具有相同的分類向量機(jī)數(shù)目。k(k-1)/2個(gè)分類向量機(jī)作為圖的中間節(jié)點(diǎn),圖中葉子節(jié)點(diǎn)為k類樣本。但在測試向量數(shù)據(jù)所屬類別時(shí),僅需經(jīng)過k-1個(gè)分類向量機(jī)節(jié)點(diǎn)即可判斷測試數(shù)據(jù)的類別。
1.2 基于二叉樹的SVM多類分類方法
在SVM多類分類算法中,分類樹是一種應(yīng)用十分廣泛的多類分類策略。但分類向量機(jī)在樹中所處的節(jié)點(diǎn)位置,直接影響到分類的準(zhǔn)確性和推廣的性能。不同的二叉樹結(jié)構(gòu),會(huì)使得測試數(shù)據(jù)得到不同的分類結(jié)果。隨著節(jié)點(diǎn)分類層次的深入,可能會(huì)產(chǎn)生分類“誤差累積”的現(xiàn)象[10]。因此,生成合適的二叉樹結(jié)構(gòu)顯得異常重要。
生成多類分類二叉樹通常包括兩種思路:第一種是依據(jù)類中樣本點(diǎn)的分布情況,優(yōu)先分出分布區(qū)域較大的類;第二種是依據(jù)類間距離作出判斷,優(yōu)先分出離其他類較遠(yuǎn)的類。而衡量類分布情況的一個(gè)有效方法是計(jì)算各個(gè)類的超球體的體積,體積越大,類的分布區(qū)域也就越大。類的超球體體積定義如下:

本文對于構(gòu)造偏二叉樹提出了類間相異度的方法,有效解決了上述問題。
2 改進(jìn)的偏二叉樹SVM多類分類方法
本文從類在空間中的分布情況和類間距離這兩方面著手,優(yōu)化分類偏二叉樹的結(jié)構(gòu)。對于類的分布情況采用參考文獻(xiàn)[11]所提出的超球體的體積來度量,而類間距離采用超球體重心間的歐氏距離來度量,關(guān)于歐氏距離的概念見定義2。為綜合考慮以上這兩個(gè)方面,本文引入了類間相異度的概念,具體內(nèi)容見定義3。

輸入:包含n個(gè)樣本對象(含分類號(hào))的數(shù)據(jù)集D。
輸出:包含K個(gè)元素的優(yōu)先分類序列S。
算法:
(1)計(jì)算每個(gè)類的最小超球體的重心和半徑;
(2)repeat;
(3)根據(jù)定義3計(jì)算每個(gè)類相對D中其他剩余類的相異度之和;
(4)選擇步驟(3)中相異度最大的類i,把類標(biāo)號(hào)i添加到S中,刪除D中類標(biāo)號(hào)為i的元素;
(5)until D中只剩兩個(gè)類的元素;
(6)把剩余的兩個(gè)類的類標(biāo)號(hào)添加到序列S中。
算法在步驟(5)返回步驟(3)循環(huán)執(zhí)行,當(dāng)數(shù)據(jù)集中僅包含兩類樣本時(shí)算法結(jié)束。
以生成分類偏二叉樹的根節(jié)點(diǎn)和左右孩子為例,取出分類序列S中第一個(gè)元素的類標(biāo)號(hào),將該類和其他類間訓(xùn)練出的向量機(jī)作為根節(jié)點(diǎn),該類作為左孩子,然后再從分類序列S中取出第二個(gè)元素的類標(biāo)號(hào),將該類和其他類間訓(xùn)練出的向量機(jī)作為右孩子。以同樣的方式生成剩余的中間節(jié)點(diǎn)和葉子節(jié)點(diǎn),最終構(gòu)建出的多類分類偏二叉樹如圖2所示。
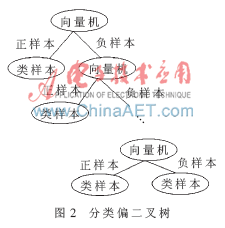
3 實(shí)驗(yàn)分析
本文所有算法均使用C++語言實(shí)現(xiàn),并使用VC6.0完成編譯。實(shí)驗(yàn)平臺(tái):Pentium?誖Dual-Core CPU 2.80 GHz、2 GB內(nèi)存、Windows XP 操作系統(tǒng)。所有實(shí)驗(yàn)數(shù)據(jù)均來自UCI數(shù)據(jù)庫中的多類別數(shù)據(jù)集vehicle和letter,具體樣本數(shù)量和維數(shù)如表1所示。

由于取不同的核參數(shù)λ和懲罰系數(shù)C[12]對模型的推廣有很大的影響,為了能更好地比較出依據(jù)不同的策略生成的偏二叉樹的推廣性能,本實(shí)驗(yàn)與參考文獻(xiàn)[12]類似,對相同數(shù)據(jù)集的每一種策略均采用多種(C,λ)參數(shù)進(jìn)行實(shí)驗(yàn),其中C的取值為2、4、8、16、32、64,λ的取值為2、4、8、16,這樣總共有6×4=24種組合,每個(gè)實(shí)驗(yàn)的KTT停止條件的容許誤差為0.001。取出最高的預(yù)測準(zhǔn)確率所對應(yīng)的(C,λ)參數(shù)及其準(zhǔn)確率進(jìn)行比較。
從實(shí)驗(yàn)數(shù)據(jù)的分析中可以看出,對于數(shù)據(jù)集vehicle,當(dāng)訓(xùn)練樣本的數(shù)量為600時(shí),在預(yù)測準(zhǔn)確率方面,使用本文提出的方法與其他方法相比,并沒有明顯的提高。而對于數(shù)據(jù)集letter,由于比vehicle數(shù)據(jù)集在訓(xùn)練時(shí)多出300個(gè)樣本,本文提出的方法在準(zhǔn)確率方面有了明顯的優(yōu)勢。總體來講,本文提出的根據(jù)類間相異度的策略生成的偏二叉樹要比單獨(dú)根據(jù)類間距離或單獨(dú)根據(jù)類樣本的分布情況生成的偏二叉樹,在準(zhǔn)確率方面有一定的改善。
基于二叉樹多類分類方法是SVM算法在多類分類問題中的一個(gè)重要應(yīng)用,但支持向量機(jī)節(jié)點(diǎn)在二叉樹中所處位置的不同對分類的準(zhǔn)確性有較大影響。本文首先分析和比較了由SVM算法所產(chǎn)生的多類分類方法,然后提出了一種依據(jù)類間相異度的策略來生成基于偏二叉樹的多類分類支持向量機(jī)。實(shí)驗(yàn)結(jié)果表明,改進(jìn)的算法在準(zhǔn)確性方面有很大的提高。
參考文獻(xiàn)
[1] VAPNIK V N.Statistical learning theory[M].New York:John Wiley and Sons,l998.
[2] 瓦普尼克.統(tǒng)計(jì)學(xué)習(xí)理論的本質(zhì)[M].張學(xué)工,譯.北京:清華大學(xué)出版社,2000.
[3] 葉磊,駱興國.支持向量機(jī)應(yīng)用概述[J].電腦知識(shí)與技術(shù),2010,6(34):153-154.
[4] 顧亞祥,丁世飛.支持向量機(jī)研究進(jìn)展[J].計(jì)算機(jī)科學(xué),2011,38(1):14-17.
[5] BOTTOU L,CORTES C,DENKER J.Comparision of classifier methods:a case study in handwriting digit recognitiong[C].Proceedings of International Conference on Pattern Recognition,1994:77-87.
[6] KRELEL U.Pairwise classification and support vector machines[M].Cambridge,MA:MIT Press,1999:255-268.
[7] 劉健,劉忠,熊鷹.改進(jìn)的二叉樹支持向量機(jī)多類分類算法研究[J].計(jì)算機(jī)工程與應(yīng)用,2010,46(33):117-120.
[8] PLATT J C,CRISTIANINI N,SHAWE-TAYLOR J.Large margin DAGs for multiclass classification[C].Advances in Neural Information Processing Systems,Cambridge,MA:MIT Press,2000:547-553.
[9] HSU C W,LIN C J.A comparsion of method for multiclass support vector machine[J]. IEEE Transaction on Neural Networks,2002,13(2):415-425.
[10] 孟媛媛,劉希玉.一種新的基于二叉樹的SVM多類分類方法[J].計(jì)算機(jī)應(yīng)用,2005,25(11):195-196,199.
[11] 唐發(fā)明,王仲東,陳錦云.支持向量機(jī)多類分類算法研究[J].控制與決策,2005,20(7):746-749.
[12] 單玉剛,王宏,董爽.改進(jìn)的一對一支持向量機(jī)多分類算法[J].計(jì)算機(jī)工程與設(shè)計(jì),2012,33(5):165-169.

