摘 要： 本文運(yùn)用網(wǎng)格環(huán)境下的并行計(jì)算模型G-PRAM來研究二叉樹的后序遍歷問題，提出了二叉樹后序遍歷的一種并行算法,，并給出示例和說明,。
關(guān)鍵詞： 網(wǎng)格環(huán)境 二叉樹 后序遍歷 并行算法
二叉樹[1]是一種重要的數(shù)據(jù)結(jié)構(gòu)，它是n(n≥0)個(gè)結(jié)點(diǎn)的有限集,。它或者是空集（n=0）,，或者由一個(gè)根結(jié)點(diǎn)和兩棵互不相交的分別稱為這個(gè)根的左、右子樹的二叉樹組成,。二叉樹的遍歷可以分為三種：一種是先序遍歷,，即先訪問二叉樹的根結(jié)點(diǎn)，然后先序遍歷左子樹,，最后先序遍歷右子樹,；第二種是中序遍歷,，即先中序遍歷左子樹，再訪問二叉樹的根結(jié)點(diǎn),，最后中序遍歷右子樹,；第三種是后序遍歷，即先后序遍歷左子樹,，再后序遍歷右子樹,，最后訪問二叉樹的根結(jié)點(diǎn)。最常見的實(shí)現(xiàn)按照遍歷過程訪問結(jié)點(diǎn),，讓每個(gè)結(jié)點(diǎn)被訪問且僅被訪問一次,，這種方式稱為串行算法。但是,，可以換個(gè)角度來研究二叉樹的遍歷問題,，即從串行算法中以二叉樹的結(jié)點(diǎn)為重點(diǎn)考察對(duì)象轉(zhuǎn)變?yōu)橹攸c(diǎn)研究二叉樹的邊的遍歷問題[2][4]。當(dāng)進(jìn)行二叉樹的一次遍歷時(shí)實(shí)際也遍歷了二叉樹的所有邊,，而且每條邊遍歷了兩次,。一次是從雙親結(jié)點(diǎn)到子結(jié)點(diǎn)，另一次則是從子結(jié)點(diǎn)到雙親結(jié)點(diǎn),。如果將每條邊變成兩條有向邊,，一條有向邊對(duì)應(yīng)向下的遍歷，另一條有向邊對(duì)應(yīng)向上的遍歷,，則遍歷二叉樹的結(jié)點(diǎn)問題變成了一個(gè)遍歷二叉樹的邊的問題,。
因?yàn)榫W(wǎng)格環(huán)境具有一般的并行環(huán)境所不具有的強(qiáng)處理能力，所以可以給每條邊分配一個(gè)獨(dú)立的處理單元（單處理器的網(wǎng)格節(jié)點(diǎn)或者多處理器網(wǎng)格節(jié)點(diǎn)的一個(gè)處理器）進(jìn)行處理,，利用多個(gè)處理單元同時(shí)對(duì)所有的邊進(jìn)行處理,，從而并行實(shí)現(xiàn)網(wǎng)格環(huán)境下的二叉樹后序遍歷。
1 網(wǎng)格環(huán)境下的G-PRAM模型
由Fortune和Wyllie形式化的PRAM[5]模型是一個(gè)理想化的并行計(jì)算模型,，被廣泛用來評(píng)估并行算法的理論性能,。PRAM的思想是假設(shè)一個(gè)共享存儲(chǔ)多處理機(jī)系統(tǒng)是由一個(gè)具有無限存儲(chǔ)容量的共享存儲(chǔ)器以及可對(duì)它進(jìn)行訪問的許多處理機(jī)所組成的系統(tǒng),。并行算法的設(shè)計(jì)者可以把處理器的能力看成是無限的,。一個(gè)PRAM由一個(gè)控制單元、全局內(nèi)存和一組處理器集合組成,。每個(gè)處理器有其自己的私有內(nèi)存,，所有處理器執(zhí)行相同的指令，但每個(gè)處理器處理的數(shù)據(jù)不同,。PRAM模型有四種,，不同之處主要在于它們處理讀寫沖突的方式有差異，包括：互斥讀互斥寫(Exclusive Read,，Exclusive Write,，EREW PRAM),，并行讀互斥寫(Concurrent Read，Exclusive Write,，CREW PRAM）,，互斥讀并行寫(Exclusive Read，Concurrent Write,，ERCW PRAM),，并行讀并行寫(Concurrent Read，Concurrent Write,，CRCW PRAM),。網(wǎng)格環(huán)境往往由相當(dāng)多的網(wǎng)格結(jié)點(diǎn)組成，這些結(jié)點(diǎn)有的是多處理器的高性能計(jì)算結(jié)點(diǎn),，有的是高容量的數(shù)據(jù)結(jié)點(diǎn),，并且往往有一個(gè)性能不錯(cuò)且容量也很大的控制結(jié)點(diǎn)。因此提出相應(yīng)的G-PRAM模型,。G-PRAM可以看作是一般PRAM的現(xiàn)實(shí)化,。
定義1 一個(gè)G-PRAM由網(wǎng)格環(huán)境下的一個(gè)控制結(jié)點(diǎn)、一個(gè)全局?jǐn)?shù)據(jù)結(jié)點(diǎn)和一組計(jì)算結(jié)點(diǎn)集合組成,。每個(gè)網(wǎng)格計(jì)算結(jié)點(diǎn)有其自己的私有內(nèi)存,，所有網(wǎng)格計(jì)算結(jié)點(diǎn)的各個(gè)處理器執(zhí)行相同的指令，但每個(gè)處理器處理的數(shù)據(jù)不一樣,。相應(yīng)的G-PRAM也有4種方式：EREW G-PRAM,、CREW G-PRAM、ERCW G-PRAM,、CRCW G-PRAM,。
2 并行實(shí)現(xiàn)二叉樹的后序遍歷
2.1 算法過程說明
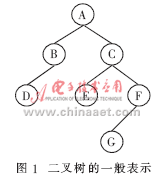
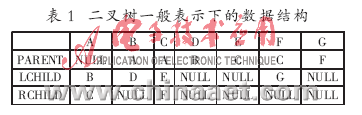
這里的算法采用并行讀互斥寫（CREW G-PRAM），算法在實(shí)現(xiàn)中對(duì)每個(gè)二叉樹結(jié)點(diǎn)保存結(jié)點(diǎn)的雙親,、左孩子和右孩子,，利用這三個(gè)參數(shù)來描述一個(gè)二叉樹結(jié)點(diǎn)在二叉樹中的相對(duì)位置。
對(duì)于如圖1所示的二叉樹,，其數(shù)據(jù)結(jié)構(gòu)描述如表1所示,。
下面分析本文中的算法步驟。
2.1.1 改造二叉樹并構(gòu)造單鏈表
首先可以將二叉樹改造成一個(gè)對(duì)應(yīng)的有向圖,。方法是將二叉樹的每條無向邊改成一條向下和另一條向上的有向邊,，結(jié)點(diǎn)不變。如圖1的二叉樹可以改造成如圖2的有向圖,。
根據(jù)改造后的有向圖構(gòu)造單鏈表的過程就是在該有向圖中尋找后繼邊的過程,，按照后序遍歷的思想，所有的處理器同時(shí)處理分配給它的一條邊的后繼邊的問題,，最終得到由全部有向邊構(gòu)成的一個(gè)單鏈表,。單鏈表的每個(gè)元素對(duì)應(yīng)于改造后的有向圖中的一條有向邊,。
設(shè)分配給處理器P[(i，j)]處理的有向邊是(i,，j),，即該邊從結(jié)點(diǎn)i指向j，則尋找有向邊(i,，j)后繼邊的問題可以根據(jù)有向邊(i,，j)的不同類型分別處理。
(1)PARENT(i)=j,，說明邊(i,，j)是一條向上邊，即從一個(gè)結(jié)點(diǎn)指向它的雙親結(jié)點(diǎn),。從數(shù)據(jù)結(jié)構(gòu)的概念中可以得到以下結(jié)論,，一條向上的邊(i，j)在二叉樹中的相對(duì)位置可以有三種情況：①結(jié)點(diǎn)j有右孩子結(jié)點(diǎn),，如圖3(a)所示,。則根據(jù)后序遍歷的思想可得邊(i，j)的后繼邊是從結(jié)點(diǎn)j指向結(jié)點(diǎn)j的右孩子結(jié)點(diǎn)構(gòu)成的邊,；②結(jié)點(diǎn)i沒有右兄弟結(jié)點(diǎn),，而結(jié)點(diǎn)j有雙親結(jié)點(diǎn)，如圖3(b)所示,。若根據(jù)后序遍歷的思想可得邊(i,，j)的后繼邊是從結(jié)點(diǎn)j指向結(jié)點(diǎn)j的雙親結(jié)點(diǎn)(parent)構(gòu)成的邊；③結(jié)點(diǎn)i既沒有兄弟結(jié)點(diǎn),，同時(shí)也沒有雙親結(jié)點(diǎn),，如圖3(c)所示，說明已經(jīng)回到了根結(jié)點(diǎn)處,，邊(i,，j)沒有后繼邊。但為了方便起見,，假設(shè)存在一條后繼邊,，從結(jié)點(diǎn)j到它自身。
(2)PARENT(i)≠j,，也就是邊(i,，j)是從雙親結(jié)點(diǎn)到它的孩子的向下的邊。
同理,，從數(shù)據(jù)結(jié)構(gòu)的概念中可以得出這樣的結(jié)論，即一條向下的邊(i,，j)在二叉樹中的位置可以有如下情況：①結(jié)點(diǎn)j有左孩子結(jié)點(diǎn)(不管有無右孩子結(jié)點(diǎn)),，如圖4(a)所示,。根據(jù)后序遍歷的思想可知，邊(i,，j)的后繼邊是從結(jié)點(diǎn)j指向結(jié)點(diǎn)j的左孩子結(jié)點(diǎn)構(gòu)成的邊,。②結(jié)點(diǎn)j沒有左孩子，但有右孩子,，如圖4(b)所示,。根據(jù)后序遍歷的思想可得，邊(i,，j)的后繼邊是從結(jié)點(diǎn)j指向結(jié)點(diǎn)j的右孩子結(jié)點(diǎn)構(gòu)成的邊,。③結(jié)點(diǎn)j沒有孩子結(jié)點(diǎn)，即結(jié)點(diǎn)j是葉子結(jié)點(diǎn),，如圖4(c)所示,。則根據(jù)后序遍歷的思想可得，邊(i,，j)的后繼邊是結(jié)點(diǎn)j指向結(jié)點(diǎn)i的向上邊,。
2.1.2 給單鏈表中的每個(gè)元素賦權(quán)值0或1
此過程也是所有的處理器同時(shí)對(duì)分配給它的一個(gè)元素賦權(quán)值（前面構(gòu)造的單鏈表中的元素）。根據(jù)后序遍歷的思想,，對(duì)于二叉樹的一個(gè)結(jié)點(diǎn)i（根結(jié)點(diǎn)例外,，必須作不同處理），如果一條向下遍歷的邊(i,，j)從結(jié)點(diǎn)i出發(fā),，則說明正在尋找從該結(jié)點(diǎn)i出發(fā)的后繼邊，結(jié)點(diǎn)i沒有被訪問,；如果一條向上遍歷的邊(i,，j)從結(jié)點(diǎn)i出發(fā)，則說明剛訪問完結(jié)點(diǎn)i,。將單鏈表中對(duì)應(yīng)向上邊的元素賦權(quán)值1（表示遍歷向上邊時(shí)增加了一個(gè)被訪問結(jié)點(diǎn)）,，對(duì)應(yīng)向下邊的元素賦權(quán)值0（表示遍歷向下邊時(shí)未增加被訪問結(jié)點(diǎn)），對(duì)應(yīng)根結(jié)點(diǎn)的環(huán)形邊元素也賦權(quán)值0（特殊處理）,。
2.1.3 計(jì)算單鏈表中各元素的位序
單鏈表中每個(gè)元素需要分配一個(gè)處理器去計(jì)算其位序,。一棵有N個(gè)結(jié)點(diǎn)的二叉樹具有（N-1）條無向邊。由于我們將每條無向邊轉(zhuǎn)換成一條向上邊和一條向下邊,，所以它共有2（N-1）條邊,，這意味著單鏈表中有2（N-1）個(gè)元素。所以,，需要2（N-1）個(gè)處理器來計(jì)算單鏈表中元素的位序,。利用計(jì)算單鏈表位序的后綴和算法可以算出單鏈表中每個(gè)元素的位序[6]。
2.1.4 求權(quán)值為1的元素的相應(yīng)結(jié)點(diǎn)的遍歷順序號(hào)
由于權(quán)值為1（向上的邊）的元素所代表的邊都是向上的邊(不妨設(shè)該邊為(i,，j)),，即結(jié)點(diǎn)i在邊(i,，j)遍歷時(shí)被訪問，而結(jié)點(diǎn)j還未被訪問,。因此,，用單鏈表中權(quán)值為1的元素的位序表示它所代表的邊(i，j)中結(jié)點(diǎn)i的位序,，從而可以得到二叉樹中全部結(jié)點(diǎn)的位序,。結(jié)點(diǎn)的位序是結(jié)點(diǎn)被訪問的先后順序的逆序。只要用結(jié)點(diǎn)個(gè)數(shù)N減去每個(gè)結(jié)點(diǎn)的位序就可以得到每個(gè)結(jié)點(diǎn)的后序遍歷順序號(hào),。與前幾步一樣,，這里也是一個(gè)處理器計(jì)算一個(gè)結(jié)點(diǎn)的順序號(hào)，多個(gè)處理器并行工作,，最后,，得到一棵二叉樹的后序遍歷的結(jié)點(diǎn)順序。
2.2 算法示意代碼
算法描述如下：
int n,； //二叉樹的結(jié)點(diǎn)個(gè)數(shù)
int parent[n],； //父結(jié)點(diǎn)數(shù)組
int lchild[n]； //左孩子結(jié)點(diǎn)數(shù)組
int rchild[n],； //右孩子結(jié)點(diǎn)數(shù)組
int succ[(n,，n)]； //后繼邊數(shù)組
int position[(n,，n)],； //鏈表元素的位序數(shù)組
int postnode[n]； //結(jié)點(diǎn)順序號(hào)數(shù)組
PostOrder(bitree *t)
//P[(i,，j)]是處理對(duì)應(yīng)邊(i,，j)的一個(gè)處理器，共2(n-1)個(gè)
{
forall P[(i,，j)] do //構(gòu)造單鏈表
{
if(lchild[j]==i)
{ if(rchild[j]!=null)
succ[(i,，j)]=(j，j.rchild),；
else if(parent[j]!=null)
succ[(i,，j)]=(j,，j.parent),；
else{
succ[(i,，j)]=(j，j),；
postnode[j]=0,；//j是根結(jié)點(diǎn)
}//else
}//if
else if(rchild[j]==i)
{ if(j.parent!=null)
succ[(i，j)]=(j，j.parent),；
else{
succ[(i,，j)]=(j,，j),；
postnode[j]=0；//j是根結(jié)點(diǎn)
}//else
}//if
else if(parent[j]==i)
{ if(lchild[j]!=null)
succ[(i,，j)]=(j,，j.lchild)；
else if(rchild[j]!=null)
succ[(i,，j)]=(j,，j.rchild)；
else succ[(i,，j)]=(j,，i)；
}//if
//給單鏈表中的每個(gè)元素賦權(quán)值
if(parent[i]==j)
position[(i,，j)]=1,；
else
position[(i，j)]=0,；
//計(jì)算單鏈表中元素的位序
where 0≤k<log(n-1)+1 do
{ position[(i,，j)]=position[(i，j)]+position[succ[(i,，j)]],；
succ[(i，j)]=succ[succ[(i,，j)]],；
}//for
if(parent[i]==j) //求結(jié)點(diǎn)的后序遍歷順序號(hào)
postnode[i]=postion[(i，j)],；
}//forall
}
3 結(jié)束語
以圖1所示的二叉樹為例,，按照上述算法構(gòu)造的單鏈表（帶權(quán)值）如圖5所示。表2為二叉樹單鏈表的位序,。
從表2中選出權(quán)值為1的邊(D,，B)、(B,，A),、(E，C),、(G,，F(xiàn))、(F，C),、(C,，A)，所以結(jié)點(diǎn)D,、B,、E、G,、F,、C、A的位序就是6,、5,、4、3,、2,、1、0,。即后序遍歷順序號(hào)是：1,、2、3,、4,、5、6,、7,，可得出后序遍歷的順序是D、B,、E,、G、F,、C,、A。
一棵有N個(gè)結(jié)點(diǎn)的二叉樹具有(N-1)條無向邊,。由于要將每條無向邊轉(zhuǎn)換成一條向上邊和一條向下邊,，所以它共有2(N-1)條有向邊。因此,，該算法需要2(N-1)個(gè)網(wǎng)格處理單元（處理器）,，而網(wǎng)格計(jì)算技術(shù)的發(fā)展為并行算法的實(shí)現(xiàn)提供了環(huán)境的支持。在本算法中求單鏈表中元素的位序的計(jì)算時(shí)間復(fù)雜度為O(logN),，而算法的其余部分的計(jì)算時(shí)間是常數(shù),，所以算法的復(fù)雜度為O(logN)。
參考文獻(xiàn)
1 嚴(yán)蔚敏，吳偉民.數(shù)據(jù)結(jié)構(gòu)(C語言版).北京：清華大學(xué)出版社,，1997
2 Tarjan R E,，Vishkin U.An efficient parallel biconnectivity algorithm.SIAM Journal of Computer，1985,；1(14)
3 Foster I.The Grid：A New Infrastructure for 21st Century Science.Physics Today,，2002；55(2)
4 熊家軍,，岳大為,，李肯立.基于SIMD-SM模型的樹的后根遍歷并行算法.計(jì)算機(jī)工程與應(yīng)用,，2002,；38(06)
5 Wilkinson B，Allen M.Parallel programming: techniques and applications using networked workstation and parallel computers.Prentice Hall Inc,，1999
6 Karp R M,，Ramachandran V.Parallel Algorithms for Shared-Memory Machines.Handbook of Theoretical Computer Science，vol A,，MIT Press,，1990