摘  要： 在室內(nèi)環(huán)境下對(duì)目標(biāo)進(jìn)行無(wú)線定位時(shí),，由于障礙物的遮擋而造成的非視距（NLOS）誤差對(duì)定位精度產(chǎn)生了很大的影響。針對(duì)此問(wèn)題,，對(duì)利用超寬帶（UWB）技術(shù)測(cè)量得到的到達(dá)時(shí)間差（TDOA）數(shù)據(jù)進(jìn)行殘差分析,，首先鑒別測(cè)得的數(shù)據(jù)中是否存在NLOS誤差，然后針對(duì)存在NLOS誤差的情況,，提出將Fang算法得到的定位結(jié)果作為泰勒級(jí)數(shù)展開(kāi)法的初始定位值,，組成Fang-Taylor級(jí)數(shù)聯(lián)合算法來(lái)計(jì)算NLOS情況下的定位結(jié)果。而對(duì)于視距（LOS）情況下測(cè)得的數(shù)據(jù),，仍采用單一的Fang算法進(jìn)行計(jì)算,。仿真對(duì)比實(shí)驗(yàn)表明,，F(xiàn)ang-Taylor級(jí)數(shù)聯(lián)合算法有效地提高了室內(nèi)NLOS環(huán)境下目標(biāo)的定位精度。
關(guān)鍵詞： 非視距,；三維定位,；Fang算法；泰勒級(jí)數(shù)展開(kāi)法

    隨著無(wú)線通信技術(shù)的高速發(fā)展,，基于無(wú)線通信的定位技術(shù)得到了廣泛的發(fā)展與應(yīng)用,。例如，眾所周知的全球定位系統(tǒng)(GPS),，在室外環(huán)境下為人們提供了許多便利,。
    相比于室外環(huán)境，室內(nèi)環(huán)境下的無(wú)線定位面臨著更多挑戰(zhàn)[1],。目前室內(nèi)定位常用的技術(shù)有超聲波,、紅外線、藍(lán)牙,、Wi-Fi、ZigBee以及近些年新興起來(lái)的技術(shù)——超寬帶（UWB）技術(shù),。其中,，超寬帶技術(shù)因其諸多優(yōu)勢(shì)而廣泛應(yīng)用在室內(nèi)定位中。超寬帶技術(shù)是一種無(wú)載波的通信技術(shù),，它利用納秒級(jí)或納秒以下的極窄脈沖信號(hào)來(lái)傳輸數(shù)據(jù),，這使得超寬帶信號(hào)有著很高的時(shí)間分辨率，進(jìn)而能夠?qū)崿F(xiàn)很高的測(cè)距精度[2],。
    用于無(wú)線定位的算法很多,，包括根據(jù)電波到達(dá)角度的AOA(Angle of Arrival)算法和信號(hào)強(qiáng)度的RSSI(Received Signal Strength Indication)算法，以及基于到達(dá)時(shí)間差的TDOA(Time Difference of Arrival)算法或到達(dá)時(shí)間的TOA(Time of Arrival)算法[3],。其中,，到達(dá)時(shí)間差的定位算法應(yīng)用較為廣泛。主要因?yàn)樗灰髠鞲衅髋c被定位目標(biāo)之間保持時(shí)鐘同步,。在無(wú)線定位技術(shù)中,，傳感器和目標(biāo)時(shí)鐘不同步是個(gè)不可消除的不利因素，而到達(dá)時(shí)間差的定位算法恰恰能克服此不利因素,，只要求傳感器之間保持時(shí)鐘同步,。因此，在室內(nèi)環(huán)境下利用到達(dá)時(shí)間差算法進(jìn)行定位計(jì)算,，從一定程度上簡(jiǎn)化了定位系統(tǒng)的復(fù)雜性,。
1 定位算法介紹
    室內(nèi)定位的過(guò)程中，在主傳感器和從傳感器時(shí)鐘同步的情況下,，利用到達(dá)時(shí)間差(TDOA)算法可以得到TDOA測(cè)量值,，然后運(yùn)用定位估計(jì)算法來(lái)處理得到的定位數(shù)據(jù),，進(jìn)而計(jì)算出最終的定位結(jié)果。具體計(jì)算過(guò)程是：利用獲得的TDOA測(cè)量值,，可以計(jì)算定位目標(biāo)和兩個(gè)傳感器之間的距離差,，多個(gè)TDOA測(cè)量值便構(gòu)成了一組關(guān)于目標(biāo)位置的雙曲面方程組，求解該雙曲面方程組就可以得到目標(biāo)的估計(jì)位置,。對(duì)于目標(biāo)位置估計(jì)的算法可以分為兩大類(lèi)：非迭代算法和迭代算法,。非迭代算法即直接算法，比較有代表性的有Chan算法[4],、Fang算法[5],；而迭代算法中比較有代表性的是泰勒級(jí)數(shù)展開(kāi)法[6]。
1.1 Fang算法
    Fang算法利用4個(gè)傳感器所得到的TDOA測(cè)量值來(lái)直接估算標(biāo)簽的位置,，這種算法計(jì)算量小,，在視距(LOS)條件下有著很高的定位精度[3-4]。該算法具體過(guò)程如下：

    在10 m×10 m×10 m的三維空間內(nèi)隨機(jī)生成待定位目標(biāo)的位置,。
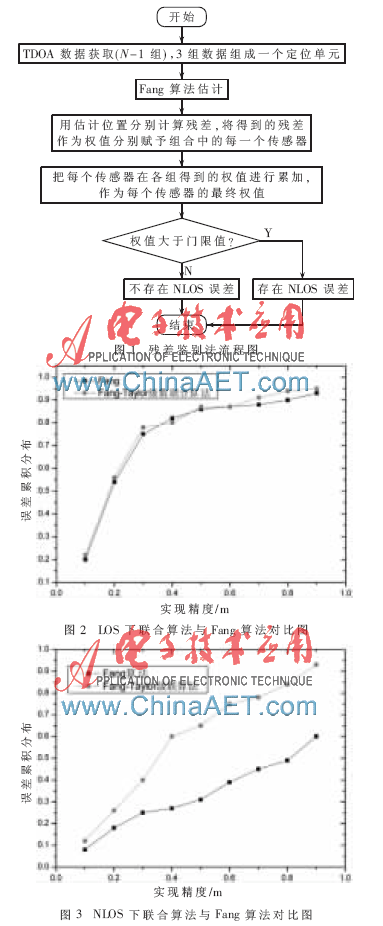
    (1)LOS環(huán)境下的仿真,。對(duì)Fang算法和Fang-Taylor聯(lián)合算法進(jìn)行實(shí)驗(yàn)仿真，對(duì)比如圖2所示,。
    從圖2可看出,， LOS環(huán)境下，F(xiàn)ang-Taylor聯(lián)合算法相比于Fang算法,，定位的性能并沒(méi)有很明顯的優(yōu)勢(shì),。
    (2)NLOS環(huán)境下的仿真。非視距誤差服從方差δ^２為0.152的高斯分布,，經(jīng)過(guò)實(shí)驗(yàn)仿真,，對(duì)比如圖3所示。
    由圖3可以看出,，在NLOS環(huán)境下,，聯(lián)合算法比Fang算法的精度有了明顯的提高，三個(gè)坐標(biāo)軸上定位結(jié)果的均方根誤差之和在0.6 m內(nèi)的概率達(dá)到了70%,。

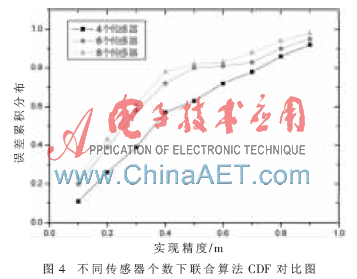
    (3)定位的傳感器個(gè)數(shù)增加至6個(gè)和8個(gè)時(shí),，結(jié)果如圖4所示。
    由圖4可以看出,，在Fang-Taylor級(jí)數(shù)聯(lián)合算法的定位計(jì)算過(guò)程中,，隨著依次增加定位傳感器的數(shù)量至4、6,、8個(gè)時(shí),，定位的精度也隨之提高。這也說(shuō)明了聯(lián)合算法在多傳感器覆蓋下的優(yōu)勢(shì)，能夠充分利用冗余的信息,。從圖4可以看出,，在3個(gè)坐標(biāo)軸上定位結(jié)果的均方根誤差之和在0.6 m內(nèi)的概率幾乎達(dá)到了80%。對(duì)比定位傳感器個(gè)數(shù)為4個(gè)和8個(gè)情況下的定位結(jié)果可以看出,，在一個(gè)定位單元內(nèi),，設(shè)置定位傳感器個(gè)數(shù)為6時(shí)，性價(jià)比最高,。

    本文通過(guò)對(duì)Fang算法和泰勒級(jí)數(shù)展開(kāi)法各自特點(diǎn)的分析,，針對(duì)室內(nèi)情況下得到的到達(dá)時(shí)間差測(cè)量數(shù)據(jù)，提出了Fang-Taylor級(jí)數(shù)聯(lián)合算法,。在定位計(jì)算開(kāi)始前,，首先對(duì)室內(nèi)環(huán)境下得到的數(shù)據(jù)進(jìn)行信道鑒別，針對(duì)室內(nèi)環(huán)境中LOS情況下得到的TDOA測(cè)量數(shù)據(jù),，運(yùn)用單一的Fang算法能快速準(zhǔn)確地給出定位結(jié)果,。而對(duì)于NLOS情況下得到的TDOA數(shù)據(jù)，則利用Fang-Taylor級(jí)數(shù)聯(lián)合算法進(jìn)行處理,。由實(shí)驗(yàn)仿真可以看出,，聯(lián)合算法有效地減小了定位誤差，而且在條件允許的情況下,，適當(dāng)增加定位傳感器的個(gè)數(shù),，可以使定位的精度得到進(jìn)一步的提高。
參考文獻(xiàn)
[1] KHOURY H M,，KAMAT V R.Indoor user localization for rapid information access and retrieval on construction sites[C]. Proceedings of the 15th Workshop of Intelligent Computing in Engineering and Architecture(EG-ICE)，Plymouth,，2008：497-507.
[2] GEZICI S,，Tian Zhi，GIANNAKIS G B,，et al.Localization  via ultra-wideband radios: a look atpositioning aspects for future sensor networks[J].IEEE Signal Processing Magazine,，2005，22(4)：70-84.
[3] CAFFERY J J,，STUBER G．Overview of radiolocation in CDMA cellular systems[J]．IEEE Communications Magazine,，1998，36(4)：35-45.
[4] CHAN Y T,，HO K C.A simple and efficient estimator for hyperbolic location[J].IEEE Transaction on Signal Processing,，1994，42(8)：1905-1915.
[5] FANG B T.Simple solutions for hyperbolic and related position fixes[J].IEEE Transaction on Aerospace and  Electronic Systems,，1990,，26(5)：748-753.
[6] FOY W H.Position location solutions by Taylor series  estimation[J].IEEE Transaction on Aerospace and Electronic  Systems，1976，12(2)：105-110.