隨著網(wǎng)絡的開放、共享及互聯(lián)程度的不斷擴大,，網(wǎng)購逐漸滲透到人們的日常生活中,，給人們帶來了便利，同時也使個人的隱私安全受到威脅,?？爝f員素質(zhì)良莠不齊，快遞員倒賣快遞單號泄露客戶個人信息的新聞屢見不鮮,。因此,，如何在快遞員速遞包裹的這一環(huán)節(jié)中保護消費者個人隱私安全是本文的主要研究內(nèi)容。

        密碼技術^[1]作為信息安全的核心技術,，主要由密碼編碼和密碼分析組成,。Diffie與Hellman在1976年發(fā)表論文“New Direction in Cryptography”,提出公開秘鑰密碼技術思想，至1977年,，第一個比較完善的RSA加密算法由Rivest、Shamir和Adleman提出,。此后,，研究人員提出了ElGamal公鑰密碼技術、橢圓曲線（ECC）^[2]公鑰密碼技術等,。至今,，RSA公鑰加密算法仍是最易理解和實現(xiàn)的一種算法，不僅可以用于加密,，也可用于數(shù)字簽名,。RSA算法的安全性主要依賴大數(shù)分解的難度。依現(xiàn)在的技術,，1 280 bit的密鑰在未來15年內(nèi)是安全的^[3],，1 024 bit的密鑰對于除了保存極為重要的數(shù)據(jù)之外在抗攻擊上也是可以接受的。不過RSA作為非對稱加密技術,，相對于對稱加密術而言,，運算速度比較慢。對于快遞這一每天處理大量數(shù)據(jù)且非常重視效率的行業(yè)來說,，加密解密速度慢會對企業(yè)和客戶造成不便,，因此尋找一種既快捷又安全的加密方式顯得尤為重要。1982年,，Quisquate和Couvreur提出了一種RSA的變型算法,，稱為RSA-CRT^[4-5]算法,，這是一種基于中國剩余定理的能夠加速RSA解密的算法。1990年,，Wiener提出了另外一種RSA的變型算法,，稱為重新平衡-RSA^[6]，進一步通過把解密成本轉(zhuǎn)移到加密成本上來加速RSA解密,。文中提出了一種基于重新平衡-RSA的變型算法,，它的公開指數(shù)e比模量更小，從而能夠在保持較低解密成本的同時有效地減少加密成本,?？梢娖湓诒ＷC信息安全的同時也提升了速度，因而十分適合應用于快遞信息的加密解密,。

1 速遞中存在的兩個安全隱患

        圖1為簡略的快遞過程,。其中造成客戶隱私泄露的環(huán)節(jié)包括兩個方面：第一，快遞公司將貼有快遞單的貨物分發(fā)到快遞公司各地配送中心的過程中,，工作人員都可以通過快遞單號在內(nèi)網(wǎng)查詢到客戶的詳細信息,，此環(huán)節(jié)中若沒有嚴格的權限限制，易造成客戶隱私泄露,；第二,，各中心快遞員將貨物派送到收貨人的環(huán)節(jié)中，快遞員能第一手獲得客戶信息,，而各快遞公司所聘快遞員素質(zhì)良莠不齊,，也易造成客戶信息的泄露。因此希望任何環(huán)節(jié)中的工作人員獲得的消費者信息越少越好,。

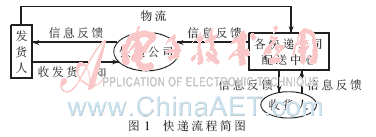
        本文將主要解決第二個環(huán)節(jié)可能帶來的隱私泄露,，即在快遞員速遞包裹的這一環(huán)節(jié)中保護消費者個人隱私安全。

        這里不考慮快遞員送包裹時使用快遞單的形式,，而是設想將快遞員當天需要送出包裹的客戶的個人信息儲存在Android系統(tǒng)的手機中并加密,，加密內(nèi)容包括客戶的名字、手機號和物品內(nèi)容等,。為了讓快遞員獲得的信息最少,，可以用家庭住址作為加密文件的文件名?？蛻粲每爝f公司事先發(fā)給客戶的一串號碼(解密密鑰)解密,，然后核對自己的信息，確認無誤后,，按確認按鈕將數(shù)據(jù)返回到快遞中心,，保證是客戶本人操作。這樣即使在手機沒有信號的時候,，快遞員因為沒有解密密鑰也無法冒充客戶收貨,。因此,，找到一種既能安全加密/解密速度又快的算法很重要。人們基于RSA算法開發(fā)了大量的加密方案與產(chǎn)品,。Jdk1.5中提供了對RSA算法的支持^[7],，所以可以在Java為支撐的安卓系統(tǒng)中實現(xiàn)RSA算法^[8]。

2 一種基于RSA的新的加密算法

        這里介紹一種基于重新平衡-RSA密鑰的生成算法,，其公開指數(shù)比要小得多,。公鑰指數(shù)e的取值范圍N^1/2<e<N。密鑰生成算法是基于以下來自數(shù)論的基本定理的,。

2.1 傳統(tǒng)重新平衡-RSA加密算法

        為了進一步提高解密速度,，Wiener提出了一種通過轉(zhuǎn)換一些加密/解密需要做的工作的變型RSA-CRT（RSA-中國剩余定理）算法，稱為重新平衡-RSA^[9],。其加密解密步驟與RSA-CRT^[10]一樣,。模數(shù)為n位，CRT指數(shù)為n_d位,，具體加密步驟如下：

        上述算法中公鑰是一對(e,，N),私鑰為元組(d_p，d_q,，p,，q)。如果按&phi;(N)的大小排序,，e大致一樣的可能性很高,。為了相對于比RSA-CRT進一步減少解密時間，則會導致加密時間幾乎最大化,。

        定理1 a和b是兩個互質(zhì)的整數(shù)且不等于1（gcd(a，b)=1且a,，b&ne;1）,。對每一個整數(shù)，存在一個唯一的有效可計算的一對整數(shù)(u_h,，v_h)滿足au_h-bv_h=1,，其中(h-1)b<u_h<hb且（h-1）a<v_h<ha。

        定理2 三元線性模塊化方程f(x,，y,，z)是具有整數(shù)系數(shù)的線性多項式。對任意&epsilon;>0,，存在正數(shù)M₀,，當任意整數(shù)M>M₀且兩個數(shù)互質(zhì)時，至少存在一個非恒定的系數(shù)f,，使得3個線性獨立的多項式f(x,，y,，z) (mod M)的每個根(x₀，y₀,，z₀)同時也是3個多項式對M取模的一個根,。若|x₀|<X，|y₀|<Y,，|z₀|<Z且XYZ<M^1-&epsilon;,，則對于一些X，Y,，Z的邊界值,，(x₀，y₀,，z₀)仍然是3個多項式中每個多項式的一個根,。如果這3個多項式代數(shù)獨立，則可以計算出(x₀,，y₀,，z₀)。

2.2 變型重新平衡-RSA算法

        以(n,，ne,，n_d)為輸入，n_e>n/2,，輸出一個有效的公鑰(e,，N)，對應的密鑰為(d_p,，d_q,，p，q),，其中|N|=n,，|e|=n_e且|d_p|=|d_q|=n_d。

        輸入：(n,，ne,，n_d)，n_e>n/2

        (1)e&larr;隨機的(ne)位奇數(shù),；

        (2)k_p1&larr;隨機的(n_d)位整數(shù)使得gcd(k_p1,，e)=1；

        (3)使用定理2(h=2),，計算(d_p,，P)使之滿足ed_p=k_p1 P+1，其中k_p1<d_p<2 k_p1,，e<Q<2e,；

        (4)P=k_p2(p-1),，k_p2是一個(n_e-n/2)位的整數(shù)，p是一個素數(shù),，如果等式不成立則返回到第(2)步,；

        (5)k_q1&larr;隨機(n_d)位；

        (6)整數(shù)gcd(k_q1,，e)=1,；

        (7)使用定理2（h=2），計算(d_q,，P)使之滿足ed_q=k_q1 Q+1,，其中k_q1<d_q<2k_q1，e<Q<2e,；

        (8)Q=k_q2(q-1),，k_q2是一個(n_e-n/2)位的整數(shù)，q是一個素數(shù),，如果等式不成立,，則返回到第(5)步。

        輸出：公鑰(e,，N),，私鑰(d_p，d_q,，p,，q)。

        從上面的算法可以看出,，它主要是由步驟(2)～(4)和步驟(5)～(7)構成的,。因此，每個循環(huán)中的迭代次數(shù)是預期的,，使得算法復雜度是線性的,。通過實驗觀察到，在n=1 024時,，每個循環(huán)迭代的次數(shù)大約為215。在每一個循環(huán)中,，試圖將一個n_e位的整數(shù)(P或Q)分解成兩個數(shù),，(n_e-n/2)位與n/2位，若想成功分解,，則需要使用橢圓曲線法(ECM),，比如，不能使(n_e-n/2)太大,，因為ECM的復雜度是基于小因子的比特長度,。因此,，必須嚴格選擇n_e，使它盡量接近n/2,，比如,，至少使(n_e-n/2)<80，因為要考慮到現(xiàn)在的計算機成功分解n_e的能力,。

2.3 不同RSA變型算法的比較

        從表1中可以看到,，當明文m=80、模為1 024位時,，從加密解密兩個方面,，將新的變型算法與其他幾個RSA算法做了一些參數(shù)比較。新算法中使用2^k+1作為加密指數(shù)的形式,，例如,，當(n_e，n_d)=(592,，190)時,，與傳統(tǒng)的重新平衡-RSA相比，加密速度提高了2.6倍,，解密速度降低了20%,。

        本文介紹了一種基于重新平衡-RSA的變型算法，可以自行選擇加密指數(shù)和CRT-指數(shù),。由表1可以看到,，新算法的加密解密消耗比例分別為4.17與0.634。對于保護快遞中的個人隱私而言,，用戶在解密時不希望花費太多時間,，這個比例適合應用于快遞中心與客戶二者之間。當然在保證一定安全的情況下,，進一步縮短加密解密時間是下一步需要研究的問題,。

參考文獻

[1] Yin Xucheng，Wu Keke,，Li Huiyun.A randomized binary modular exponentiation based RSA algorithm against the comparative power analysis[C].In：Proceedings of 2012 IEEE International Conference on Intelligent Control,，Automatic Detection and High-End Equipment（ICADE 2012），2012：160-165.

[2] 徐茂智, 游林.信息安全與密碼學[M].北京：清華大學出社,，2007.

[3] JOCHEMZ E,，MAY A.A polynomial time attack on RSA  with private CRT-exponents smaller than N0.073[C].In：Proceeding of Crypto 2007，LNCS 4622,，Berlin：Springer-Verlag,，2007：395-411.

[4] 王保倉，韋永壯，胡予濮.基于中國剩余定理的快速公鑰加密算法[J].西安電子科技大學學報(自然科學版),，2008,，35(3)：449-454.

[5] 劉承斌，耿也,，舒奎,，等.有關中國剩余定理在多個素數(shù)的RSA解密運算中的加速公式的論證以及加速效率的估算[J].大連工業(yè)大學學報，2012,，31(5)：372-375.

[6] Sun Hungmin,，Wu Muen，HINEK M J,，et al.Trading decryption for speeding encryption in Rebalanced-RSA[J].The Journal of Systems and Software 82,，2009，82(9)：1503-1512.

[7] 趙軍.基于Android平臺加密算法的研究與實現(xiàn)[D].南京：南京理工大學,，2012.

[8] 司光東,，楊加喜，譚示崇,，等.RSA算法中的代數(shù)結構[J].電子學報,，2011，39(1)：242-246.

[9] Liu Qing,，Li Yunfei,，Li Tong，et al.The research of the batch RSA decryption performance[J].Journal of Computation Information Systems,，2011,，7(3)：948-955.

[10] Sun Jin，Hu Yupu.Identity-based broadcast encryption scheme using the new techniques for dual system encryption[J].Journal of Electronics & Information Technology,，2011,，33(5)：1266-1270.