文獻(xiàn)標(biāo)識(shí)碼： A
文章編號(hào)： 0258-7998(2014)07-0061-04
摘 要： 為了提升密碼算法中非線性布爾函數(shù)實(shí)現(xiàn)效率,，設(shè)計(jì)了串行與電路和以查找表為基礎(chǔ)的并行化低次布爾函數(shù)實(shí)現(xiàn)架構(gòu)，分別實(shí)現(xiàn)高次與項(xiàng)和低次與項(xiàng),。分析了不同并行化查找表實(shí)現(xiàn)密碼算法中低次布爾函數(shù)的效率,。結(jié)果表明，結(jié)合香農(nóng)分解定理提出的并行化查找表架構(gòu)處理性能可以達(dá)到1.02 GHz,，不僅能夠靈活適配密碼算法中的非線性布爾函數(shù),，而且能夠節(jié)省資源占用。
關(guān)鍵詞： 非線性布爾函數(shù),；查找表,；并行化；適配
在對(duì)稱密碼算法中,，非線性布爾函數(shù)起著舉足輕重的作用,，其實(shí)現(xiàn)效率直接決定密碼算法的處理效率。非線性布爾函數(shù)的實(shí)現(xiàn)主要有基本邏輯運(yùn)算組合實(shí)現(xiàn),、可編程的與-異或陣列和查找表3種方式實(shí)現(xiàn),。其中基本邏輯運(yùn)算組合實(shí)現(xiàn)主要應(yīng)用于通用處理器中，通過(guò)多種基本運(yùn)算組合,，可以實(shí)現(xiàn)任意形式的非線性布爾函數(shù),。可編程與-異或陣列[1-2]采取對(duì)陣列進(jìn)行遍歷的方式實(shí)現(xiàn)不同的布爾函數(shù),，通過(guò)增加陣列的維度以適配更多變量的布爾函數(shù),。查找表[3-4]采取將真值表預(yù)存的方式實(shí)現(xiàn)布爾函數(shù)，通過(guò)增加存儲(chǔ)資源來(lái)適配更多變量的布爾函數(shù),，也可以將高次布爾函數(shù)分解,，通過(guò)多級(jí)運(yùn)算的方式實(shí)現(xiàn)。
可編程與-異或陣列和查找表的出現(xiàn),，雖然在一定程度上緩解了非線性布爾函數(shù)實(shí)現(xiàn)效率低下的問(wèn)題,，但針對(duì)密碼算法中的非線性布爾函數(shù),，以上兩種方式均沒(méi)有充分利用密碼算法中非線性布爾函數(shù)的特點(diǎn)，也未充分開(kāi)發(fā)可編程與-異或陣列和查找表的并行性,，導(dǎo)致存儲(chǔ)資源的利用率低,，適配能力不足。
本文通過(guò)對(duì)密碼算法中的非線性布爾函數(shù)特點(diǎn)進(jìn)行分析,，分別針對(duì)大與項(xiàng)少和小與項(xiàng)多的特點(diǎn),，設(shè)計(jì)了并行化的查找表架構(gòu)，能夠適配最大與項(xiàng)次數(shù)為6的非線性布爾函數(shù),；針對(duì)高次與項(xiàng)少的特點(diǎn),，設(shè)計(jì)了專門(mén)的串行與運(yùn)算,，可以適配任何次數(shù)的與項(xiàng),，能夠有效提升非線性布爾函數(shù)的實(shí)現(xiàn)效率。
1 非線性布爾函數(shù)特征分析
1.1 非線性布爾函數(shù)操作特征分析
分別從非線性布爾函數(shù)的狀態(tài)序列長(zhǎng)度,、變量個(gè)數(shù),、與項(xiàng)最高次數(shù)以及與項(xiàng)個(gè)數(shù)等方面對(duì)密碼算法中的非線性布爾函數(shù)操作特征進(jìn)行了統(tǒng)計(jì)分析和總結(jié)歸納，如表1[5-7]所示,。
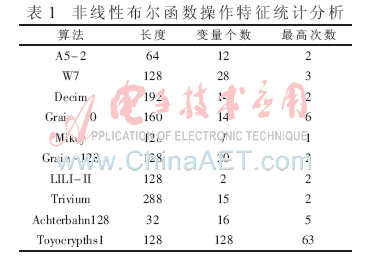
結(jié)合表1和非線性布爾函數(shù)多項(xiàng)式的表示形式,，可以得出密碼算法中的非線性布爾函數(shù)具有以下幾個(gè)特點(diǎn)：
(1)狀態(tài)序列長(zhǎng)度，即可能出現(xiàn)在非線性布爾函數(shù)中的所有變量個(gè)數(shù),，不同算法中差異較大,。
(2)變量個(gè)數(shù)。非線性布爾函數(shù)狀態(tài)序列較長(zhǎng),，并不是所有變量均參與非線性布爾函數(shù)的運(yùn)算,，如在Grain128算法中，參與運(yùn)算的變量只有總變量的7.8%左右,，但變量位置比較分散,。
(3)與項(xiàng)次數(shù)。參與非線性布爾函數(shù)運(yùn)算的與項(xiàng)次數(shù)差異較大,。
(4)與項(xiàng)個(gè)數(shù),。算法中的非線性布爾函數(shù)中出現(xiàn)的與項(xiàng)種類(lèi)在變量可能組成的與項(xiàng)種類(lèi)中所占比例較小。
(5)與項(xiàng)之間關(guān)系,。與項(xiàng)之間均為異或關(guān)系,，不同的與項(xiàng)中可能重復(fù)出現(xiàn)相同的變量，與項(xiàng)之間的變量通常具有交叉或包含關(guān)系,。
1.2 非線性布爾函數(shù)的分類(lèi)
由圖1可知,，密碼算法中的非線性布爾函數(shù)具有參與運(yùn)算的變量占所有變量比例小、變量位置分散,、高次與項(xiàng)少,、低次與項(xiàng)多的特點(diǎn),。將不同的變量組成的與項(xiàng)進(jìn)行組合可以發(fā)現(xiàn)，整個(gè)非線性布爾函數(shù)可以拆分為多個(gè)包含較少變量的非線性布爾函數(shù)(少變量布爾函數(shù)),，只是變量的表現(xiàn)形式和變量之間的組合不同,。若對(duì)非線性布爾函數(shù)進(jìn)行拆分，則能夠有效地減少實(shí)現(xiàn)介于低次與項(xiàng)和高次與項(xiàng)中間布爾函數(shù)消耗的資源,，降低路徑延遲,。需要針對(duì)少變量布爾函數(shù)的運(yùn)算進(jìn)行專門(mén)的設(shè)計(jì)。高次與項(xiàng)較少,，需設(shè)計(jì)專門(mén)的串行與電路實(shí)現(xiàn),。
與-異或陣列實(shí)現(xiàn)方式雖然不需要關(guān)心變量的形式，但當(dāng)與項(xiàng)較多時(shí),，需要的配置信息量十分龐大,，極大地降低了實(shí)現(xiàn)的靈活性。查找表實(shí)現(xiàn)方式不需要關(guān)心變量的位置,，只需要考慮變量的個(gè)數(shù),，且配置信息量較小，比較適合實(shí)現(xiàn)少變量非線性布爾函數(shù),。只需將多個(gè)少變量布爾函數(shù)的結(jié)果相異或,，即可實(shí)現(xiàn)布爾函數(shù)中所有低次與項(xiàng)計(jì)算。但常見(jiàn)的非線性布爾函數(shù)實(shí)現(xiàn)方式不能支持多個(gè)布爾函數(shù)的同時(shí)輸出,，造成了資源的浪費(fèi)和性能的降低,。基于此,，為充分開(kāi)發(fā)設(shè)計(jì)的布爾函數(shù)架構(gòu)的并行性,，將低次布爾函數(shù)中與項(xiàng)的種類(lèi)分為兩類(lèi)，并以此為基礎(chǔ),，研究低次與項(xiàng)的并行化實(shí)現(xiàn)架構(gòu)：
(1)無(wú)公共變量
無(wú)公共變量指的是各與項(xiàng)之間不存在公共變量,，與項(xiàng)之間相互獨(dú)立。如日本的TOYOCRYPT-HS1算法中非線性布爾函數(shù),，包含63個(gè)二次與項(xiàng),，與項(xiàng)之間無(wú)公共變量。
(2)有公共變量
有公共變量指的是各與項(xiàng)之間存在公共變量,，且公共變量的個(gè)數(shù)差異較大,，與項(xiàng)之間的公共變量差異也較大。如Grain80算法中濾波函數(shù),，包含3個(gè)二次與項(xiàng),，每?jī)蓚€(gè)與項(xiàng)之間都有一個(gè)相同的變量，包含4個(gè)三次與項(xiàng),，存在有兩個(gè)共有變量的情況,。
2 并行化非線性布爾函數(shù)實(shí)現(xiàn)架構(gòu)
結(jié)合密碼算法中非線性布爾函數(shù)中與項(xiàng)的特點(diǎn),，分別針對(duì)布爾函數(shù)中不同與項(xiàng)的特點(diǎn)，提出相應(yīng)的布爾函數(shù)實(shí)現(xiàn)方式,。
2.1 高次與項(xiàng)實(shí)現(xiàn)
密碼算法中非線性布爾函數(shù)高次與項(xiàng)數(shù)量較少,，因此設(shè)計(jì)了專門(mén)的串行與電路實(shí)現(xiàn)，如圖1所示,?？梢酝ㄟ^(guò)控制序列C中1選擇源序列S相應(yīng)的數(shù)據(jù)，將保留的數(shù)據(jù)進(jìn)行相與,，即可得到高次與項(xiàng)的結(jié)果,。當(dāng)與項(xiàng)次數(shù)i大于N時(shí)，可以將控制序列C中填充為全1,，i(mod N)不為0時(shí),，最后一組控制序列不需要為全1，按照實(shí)際需求進(jìn)行配置,。
2.2 低次與項(xiàng)實(shí)現(xiàn)
低次與項(xiàng)的布爾函數(shù)其與項(xiàng)之間的關(guān)系主要包含無(wú)公共變量,、有公共變量2種，分別對(duì)兩類(lèi)與項(xiàng)的實(shí)現(xiàn)進(jìn)行了研究,，并在此基礎(chǔ)上提出了改進(jìn)的并行化實(shí)現(xiàn)架構(gòu)。
2.2.1 無(wú)公共變量類(lèi)與項(xiàng)實(shí)現(xiàn)
無(wú)公共變量類(lèi)與項(xiàng)中各與項(xiàng)之間無(wú)化簡(jiǎn)的空間,，可以采用傳統(tǒng)的查找表方式實(shí)現(xiàn),。由于與項(xiàng)的次數(shù)不固定，因此對(duì)查找表實(shí)現(xiàn)方式進(jìn)行了并行化設(shè)計(jì),，以提高資源的利用率,。
采用單一查找表方式實(shí)現(xiàn)變量數(shù)位n的非線性布爾函數(shù)需要的存儲(chǔ)空間為2n，即可以滿足兩個(gè)變量為n-1的布爾函數(shù)所需存儲(chǔ)空間,，滿足4個(gè)變量數(shù)為n-2的布爾函數(shù)所需存儲(chǔ)空間,，依此類(lèi)推可以滿足2n-m個(gè)變量數(shù)為m的布爾函數(shù)所需存儲(chǔ)空間。結(jié)合密碼算法中布爾函數(shù)的特點(diǎn),，本文以6為例,，對(duì)布爾函數(shù)的并行化設(shè)計(jì)進(jìn)行分析。
通過(guò)分析在26存儲(chǔ)空間上如何實(shí)現(xiàn)4變量,、5變量,、6變量函數(shù)，提出了并行化布爾函數(shù)設(shè)計(jì)電路,，包含輸入端口和配置端口,，通過(guò)不同的配置，可以支持4個(gè)無(wú)公共變量的4變量布爾函數(shù),，2個(gè)無(wú)公共變量的5 變量布爾函數(shù)，1個(gè)6變量的布爾函數(shù),，如圖2所示,。可以充分利用電路中的存儲(chǔ)資源,，尤其是當(dāng)要實(shí)現(xiàn)的布爾函數(shù)具有變量個(gè)數(shù)多、與項(xiàng)次數(shù)低的特征時(shí),，可以將布爾函數(shù)分別實(shí)現(xiàn),，然后將函數(shù)的運(yùn)算結(jié)果進(jìn)行異或即可。
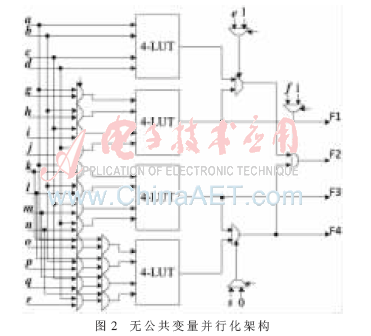
2.2.2 有公共變量類(lèi)與項(xiàng)實(shí)現(xiàn)
無(wú)公共變量的并行化架構(gòu)靈活性高,，實(shí)現(xiàn)布爾函數(shù)種類(lèi)多,，但輸入端口數(shù)較多，不利于處理器中集成,。密碼算法的布爾函數(shù)中與項(xiàng)存在大量的公共變量,，若充分利用公共變量的特點(diǎn)，則能夠有效降低布爾函數(shù)實(shí)現(xiàn)中所需的端口,。如以6變量布爾函數(shù)為例,，支持圖2所具有的功能，公共變量數(shù)為n(n<6),，則輸入端口數(shù)減少為19-3n,。
基于此提出了具有2個(gè)公共變量的并行化架構(gòu)，如圖3所示,。以具有2個(gè)公共變量的6變量布爾函數(shù)的實(shí)現(xiàn)為例,，可以支持4組具有2個(gè)公用變量的4變量布爾函數(shù)，分別為f(a,，b,，c，d),，f(a,，b，g,，h),，f(a，b,，m,，n)，f(a,，b,，p，q)；支持2組具有2個(gè)公用變量的5變量布爾函數(shù),，分別為f(a,，b，c,，d,，e)，f(a,，b,，m，n,，s),；支持一個(gè)6變量布爾函數(shù)f(a，b,，c,，d，e,，f),。
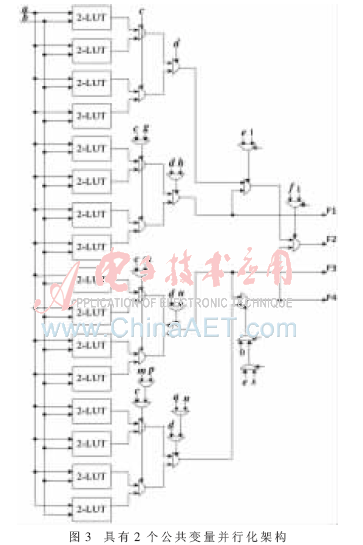
2.2.3 改進(jìn)的布爾函數(shù)的實(shí)現(xiàn)結(jié)構(gòu)
具有2個(gè)公共變量并行化架構(gòu)能夠有效地減少輸入端口的數(shù)量，但不能減少存儲(chǔ)資源的消耗,。若能充分利用密碼算法中非線性布爾函數(shù)具有0,、1因子的特點(diǎn)，可以有效地降低實(shí)現(xiàn)所需的資源消耗,?；诖耍Y(jié)合香農(nóng)分解定理和低次與項(xiàng)具有公共變量的特點(diǎn),，提出了改進(jìn)的具有2個(gè)公共變量的并行化架構(gòu)。
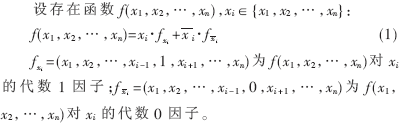
由式(1)可知,，當(dāng)一個(gè)n變量布爾函數(shù)存在代數(shù)1,、0因子時(shí)，n變量的布爾函數(shù)可以分解為n-1變量和n-2變量的兩個(gè)非線性布爾函數(shù),，從而可將一個(gè)n變量布爾函數(shù)所需的2n比特存儲(chǔ)資源降少到2n-1+2n-2比特資源,，如圖4所示并行化架構(gòu)，以具有2個(gè)公共變量的6變量布爾函數(shù)的實(shí)現(xiàn)為例,，可以同時(shí)支持3組具有2個(gè)公用變量的4變量布爾函數(shù),，分別為f(a，b,，c,，d)，f(a，b,，f,，g)，f(a,，b,，m，n),；支持具有一個(gè)公用變量的5變量布爾函數(shù)和一個(gè)4變量布爾函數(shù),，分別為f(a，b,，c,，d，e),，f(a,，b，m,，n),；支持一個(gè)具有代數(shù)0、1因子的6變量布爾函數(shù)f(a,，b,，c，d,，e,，f)。
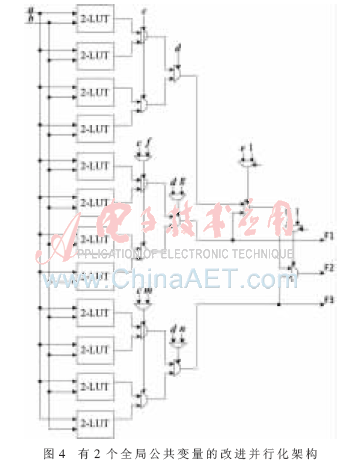
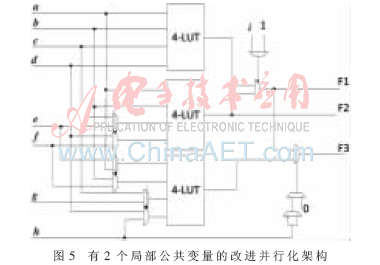
圖4中的非線性布爾函數(shù)實(shí)現(xiàn)方式雖然有效降低了輸入端口數(shù)和存儲(chǔ)資源的占用,，但其支持的所有布爾函數(shù)均存在公共變量,。為了在接口數(shù)量不變的情況下支持更多類(lèi)型的布爾函數(shù)種類(lèi)，對(duì)圖4進(jìn)行了改進(jìn),，如圖5所示,，可以支持支持3組具有2個(gè)公用變量的4變量布爾函數(shù)，分別為f(a,，b,，c，d),，f(a,，b，e,，f),，f(a，b，g,，h),；支持無(wú)公用變量的5變量布爾函數(shù)和4變量布爾函數(shù)，分別為f(a,，b,，c，d,，i),，f(e，f,，g,，h)；支持一個(gè)具有代數(shù)0,、1因子的6變量布爾函數(shù)f(a,，b，c,，d,，h，i),。
3 函數(shù)適配與性能分析
為了驗(yàn)證所設(shè)計(jì)架構(gòu)的正確性和高效性,，對(duì)密碼算法中的非線性布爾函數(shù)進(jìn)行了適配，選取了grain-80算法中的非線性布爾函數(shù),。設(shè)初始的序列已經(jīng)按照布爾函數(shù)的要求將變量進(jìn)行排列：
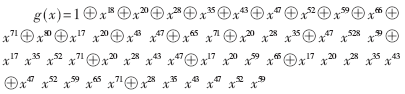
如表2所示,，可以看出，4種并行化架構(gòu)都能高效地適配密碼算法中的非線性布爾函數(shù),，而密碼算法中的非線性布爾函數(shù)具有代數(shù)0,、1因子的特征比較明顯，兩種改進(jìn)的非線性布爾函數(shù)架構(gòu)就可以很好地滿足密碼算法中布爾函數(shù)的需求,，最高處理速度可以達(dá)到1.02 GHz,，資源占用是其他實(shí)現(xiàn)方式的75%。由于其端口數(shù)和存儲(chǔ)資源占用均較小,，特別適合集成到專用的密碼處理器中。
結(jié)果表明,，本文設(shè)計(jì)的非線性布爾函數(shù)并行化架構(gòu)有效滿足了密碼算法中非線性布爾函數(shù)的特點(diǎn),，不僅可以靈活地適配密碼算法中的非線性布爾函數(shù)，同時(shí)具有較高的處理性能,。
通過(guò)分析密碼算法中非線性布爾函數(shù)的特點(diǎn),，對(duì)布爾函數(shù)中與項(xiàng)進(jìn)行分類(lèi)；針對(duì)不同類(lèi)別的與項(xiàng)，提出了相應(yīng)的并行化布爾函數(shù)實(shí)現(xiàn)架構(gòu),。在此基礎(chǔ)上,，結(jié)合香農(nóng)定理，提出了改進(jìn)的并行化非線性布爾函數(shù)實(shí)現(xiàn)架構(gòu),，能夠在較少的輸入端口和資源占用情況下靈活適配密碼算法中的非線性布爾函數(shù),。
下一步需要針對(duì)不同應(yīng)用場(chǎng)景下非線性布爾函數(shù)的特點(diǎn)，設(shè)計(jì)相應(yīng)的并行化架構(gòu),，提高不同場(chǎng)景下非線性布爾函數(shù)的處理速度,。
參考文獻(xiàn)
[1] HUTTON M，Sshilecher J.Improving FPGA performance and area using an adaptive logic module[C].Berlin Heidelberg：J Becker,，2004：135-144.
[2] Xu Liqing,，Chen Hao.Some results on the algebraic immunity of Boolean functions[J].The Journal of China Universities of Posts and Telecommunications，2011,，18(2)：102-105.
[3] KAVUT S,，YUCEL M D.9-variable Boolean functions with nonlinearity 242 in the generalized rotation symmetric class[J].Information and Computation, 2010，208(4): 341–350.
[4] GANGOPADHYAY S,，SARKAR S.Telang R.On the lower bounds of the second order nonlinearities of some Boolean functions[J].Information Science,， 2010，180(2)：266-273.
[5] CHASKHKM A V.Local complexity of Boolean functions[J].Discrete Applied Mathematics[J].2004,，135(1): 55-64.
[6] COUCEIRO M,，MARICHAL J L.Locally monotone Boolean and pseudo-Boolean functions[J].Discrete Applied Mathematics，2012,，160(12)：1651-1660.
[7] 徐建博,戴紫彬.面向序列密碼抽取與插入單元可重構(gòu)設(shè)計(jì)研究[J].電子技術(shù)應(yīng)用,，2011，37(7)：65-67.