自然風(fēng)速的隨機(jī)性和風(fēng)電機(jī)組的強(qiáng)非線性使風(fēng)機(jī)輸出功率不穩(wěn)定,。風(fēng)速低于額定值時(shí),，機(jī)組的控制目標(biāo)為最大風(fēng)能捕獲^[1]；風(fēng)速高于額定值時(shí),，通過槳距角的調(diào)節(jié),，改變風(fēng)能利用系數(shù)，使輸出功率恒定^[2],。參考文獻(xiàn)[3]采用微分幾何將風(fēng)電模型線性化再結(jié)合H∞控制理論設(shè)計(jì)恒功率控制器,，參考文獻(xiàn)[4]將微分幾何線性化與極點(diǎn)配置結(jié)合設(shè)計(jì)變槳距控制器。此外,，滑模變結(jié)構(gòu)^[5],、自抗擾^[6]、自適應(yīng)模糊^[7]等也在風(fēng)電系統(tǒng)中得到應(yīng)用,。本文將精確反饋線性與模糊理論有機(jī)結(jié)合,，設(shè)計(jì)變槳控制器并仿真，結(jié)果表明,，該控制器能有效,、迅速地穩(wěn)定不確定風(fēng)電系統(tǒng)，性能良好,。

1 風(fēng)電機(jī)組模型

    風(fēng)力機(jī)模型：

其中：

    由(1),、(5)可知該風(fēng)力發(fā)電系統(tǒng)的數(shù)學(xué)模型為：

    當(dāng)風(fēng)速在額定值之上時(shí)，控制目標(biāo)是輸出恒功率,。把風(fēng)機(jī)角速度的變化作為控制器的輸入,，在變槳距控制器的作用下改變槳距角，從而改變風(fēng)能的利用系數(shù),，將風(fēng)力機(jī)的轉(zhuǎn)速控制在額定值附近,，則輸出功率限定在額定值,。風(fēng)力發(fā)電系統(tǒng)的變漿距控制框圖如圖1所示。

2 基于微分幾何的風(fēng)電系統(tǒng)全局線性化

2．1 精確反饋線性化理論^[8]

    單輸入單輸出的仿射非線性系統(tǒng)：

    則系統(tǒng)(6)被轉(zhuǎn)化為：

3 模糊控制器的設(shè)計(jì)

    由式（14）知這是一個(gè)兩輸入單輸出的系統(tǒng),。在該系統(tǒng)中,，狀態(tài)量z₁的物理含義為風(fēng)力機(jī)的轉(zhuǎn)速ω_r，z₂的物理意義為ωr的變化率所以模糊控制器的輸入即為風(fēng)力機(jī)實(shí)際轉(zhuǎn)速與額定轉(zhuǎn)速的誤差e及誤差變化率ec,，輸出為控制定律v,。

    誤差的變化范圍為[-0.5，0.5],，令語言變量E的論域X＝{-3,，-2，-1,，0,，1，2,，3},，從而e的量化因子K_e＝6。為語言變量E選取7個(gè)語言值分別為NB,、NM,、NS、ZO,、PS,、PM、PB,，由經(jīng)驗(yàn)可得出相應(yīng)隸屬函數(shù),，從而可得出語言變量的賦值表如表1所示。

    設(shè)ec的范圍為[-0.06,，0.06]，選EC的論域Y＝{-3,，-2,，-1，0,，1,，2，3},，則得誤差ec的量化因子K_ec＝50,。同時(shí)語言變量EC也選取7個(gè)語言值為NB、NM,、NS,、ZO,、PS、PM,、PB,，則其語言變量EC的賦值表與E的相同，即表1所示,。

    設(shè)v的范圍[-3,，3]，令V的論域Z＝{-3,，-2,，-1，0,，1,，2，3},，則v的比例因子K_v＝1,。為語言變量V也選取7個(gè)語言值分別為NB、NM,、NS,、ZO、PS,、PM,、PB，則其語言變量的賦值表與EC和E的相同,，即表1所示,。

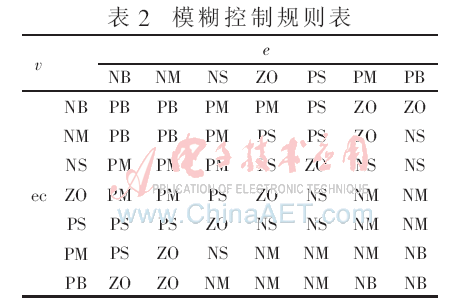
    對(duì)所有變量賦值后，下一步是模糊控制表的編寫,。根據(jù)風(fēng)機(jī)角速度的誤差及誤差的變化率來確定控制器的輸出,。

    若風(fēng)機(jī)角速度的誤差與角加速度的誤差變化趨勢(shì)相同，都為正大或正中（?。?，意味著風(fēng)機(jī)角速度有繼續(xù)變大的趨勢(shì)，所以控制器應(yīng)輸出負(fù)大或負(fù)中,，以減小角速度的誤差,，使之趨于額定值。同理,，若風(fēng)機(jī)角速度的誤差及誤差變化率都為負(fù)大或負(fù)中（?。瑒t控制器輸出應(yīng)為正大或正中。

    若風(fēng)機(jī)角速度的誤差與其角加速度的誤差變化趨勢(shì)相反,，即角速度為正（負(fù)）而角加速度為負(fù)（正）時(shí),，可以看出系統(tǒng)本身已經(jīng)向平衡狀態(tài)調(diào)整，所以分別取較小的控制量,。尤其當(dāng)兩者一個(gè)為正大（中,、小）,，而另一個(gè)為負(fù)大（中,、小）時(shí),，控制量取為0,。

    若風(fēng)機(jī)角速度誤差與角加速度的誤差其中有一個(gè)為0，則系統(tǒng)必在穩(wěn)態(tài)附近,，所以控制量取較小的值,。

    由以上分析得到模糊控制表如表2所示，可得原系統(tǒng)的非線性模糊變槳距控制器,。

4 結(jié)果與分析

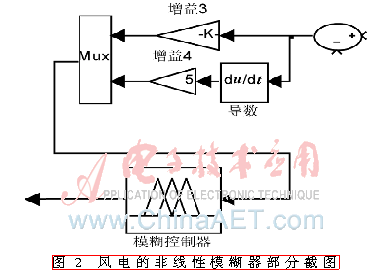
    如圖2所示,，在MATLAB/Simulink中建模并仿真，結(jié)果如圖3和圖4所示,。

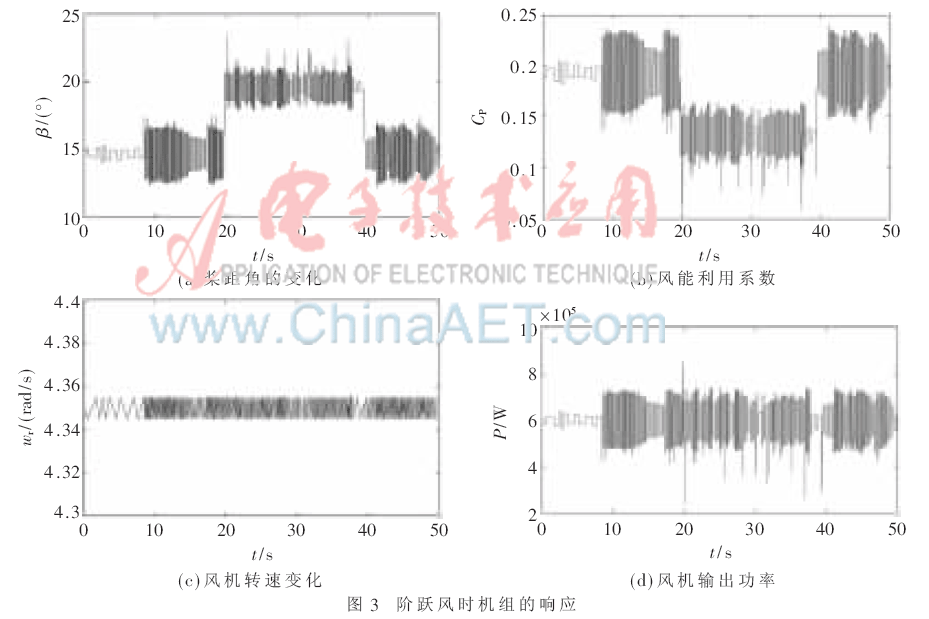
    (1)風(fēng)速在15 m/s～17 m/s之間階躍變化時(shí)的機(jī)組響應(yīng)如圖3所示,。由圖3可以看出，當(dāng)風(fēng)速階躍增大時(shí),，槳距角也發(fā)生相應(yīng)變化,，從15°增加到20°左右。同時(shí)風(fēng)能利用系數(shù)減小了,，從0.2減到0.13左右,，從而減少了系統(tǒng)風(fēng)能的捕獲，將風(fēng)機(jī)角速度限定在4.35 rad/s,，同時(shí)系統(tǒng)功率限定在600 kW左右,。

    (2)風(fēng)速在15 m/s～16 m/s之間隨機(jī)變化時(shí)的機(jī)組響應(yīng)如圖4所示。由圖4可知,，在隨機(jī)風(fēng)速下,，控制器也能將輸出功率控制在額定值600 kW左右，實(shí)現(xiàn)了控制功能,。

    本文利用微分幾何原理對(duì)強(qiáng)非線性風(fēng)電模型進(jìn)行精確反饋線性化，再結(jié)合模糊理論,，設(shè)計(jì)了模糊控制器,。在MATLAB中建模并仿真，可知當(dāng)風(fēng)速在額定值以上變化時(shí)，控制器能通過調(diào)節(jié)槳距角來改變風(fēng)能利用系數(shù),，使風(fēng)機(jī)的角速度和系統(tǒng)功率穩(wěn)定在恒值附近,，體現(xiàn)了該模糊變槳距控制器的良好性能。但該控制器無法將輸出功率嚴(yán)格穩(wěn)定在600 kW,，故還需改進(jìn),。

參考文獻(xiàn)

[1] 王琦，陳小虎,，紀(jì)延超,，等.基于雙同步坐標(biāo)的無刷雙饋風(fēng)力發(fā)電系統(tǒng)的最大風(fēng)能追蹤控制[J].電網(wǎng)技術(shù)，2007,，31(3)：82-87.

[2] 葉杭冶.風(fēng)力發(fā)電機(jī)組的控制技術(shù)[M].北京：機(jī)械工業(yè)出版社.2006

[3] 秦生升,，胡國(guó)文，顧春雷,，等.風(fēng)力發(fā)電系統(tǒng)的恒功率非線性H∞魯棒控制[J].控制理論與應(yīng)用,，2012，29(5)：617-622.

[4] 楊俊華,，鄭儉華,，楊夢(mèng)麗，等.變槳距風(fēng)力發(fā)電機(jī)組恒功率反饋線性化控制[J].控制理論與應(yīng)用,，2012,，29(10)：1365-1370.

[5] 郭慶鼎，趙麟,，郭洪澈.1MW變速變距風(fēng)力發(fā)電機(jī)的滑模變結(jié)構(gòu)魯棒控制[J].沈陽(yáng)工業(yè)大學(xué)學(xué)報(bào),，2005，27(2)：171-174,，186.

[6] 夏長(zhǎng)亮,，宋戰(zhàn)鋒.雙饋風(fēng)力發(fā)電系統(tǒng)轉(zhuǎn)子電流自抗擾控制[J].電工電能新技術(shù)，2007,，26(3)：11-14,，19.

[7] 張新房，徐大平,，呂躍剛,，等.大型變速風(fēng)力發(fā)電機(jī)組的自適應(yīng)模糊控制[J].系統(tǒng)仿真學(xué)報(bào)，2004,，16(3)：574-577.

[8] 盧強(qiáng),，孫元章.電力系統(tǒng)非線性控制[M].北京：科學(xué)出版社，2008.