摘  要： 將神經(jīng)元自適應(yīng)的控制模型與常規(guī)PID控制算法相結(jié)合，設(shè)計(jì)了一種自適應(yīng)PID控制器,，并將其應(yīng)用于風(fēng)力發(fā)電機(jī)試驗(yàn)系統(tǒng)電源組的控制系統(tǒng)中。該控制器不僅結(jié)構(gòu)簡(jiǎn)單,、參數(shù)易于整定,，且具有較好的自適應(yīng)和自學(xué)習(xí)功能,。結(jié)果表明，應(yīng)用神經(jīng)元PID控制的風(fēng)力發(fā)電機(jī)試驗(yàn)系統(tǒng)的電源組控制系統(tǒng)能夠適應(yīng)被控對(duì)象在較大范圍內(nèi)的變化,，具有較強(qiáng)的自適應(yīng)性和優(yōu)良的控制性能。

　　關(guān)鍵詞： 試驗(yàn)系統(tǒng),；風(fēng)力發(fā)電機(jī),；神經(jīng)元自適應(yīng)控制,；PID控制

　　目前風(fēng)力發(fā)電試驗(yàn)系統(tǒng)所使用的電源控制系統(tǒng),，其調(diào)節(jié)對(duì)象具有時(shí)變性、多樣性,、不確定性和非線性等特點(diǎn)，因此針對(duì)該試驗(yàn)電源組控制系統(tǒng)難以建立精確的數(shù)學(xué)模型,，而且試驗(yàn)電源組控制系統(tǒng)的動(dòng)態(tài)特性及運(yùn)行參數(shù)依賴于它的運(yùn)行環(huán)境與運(yùn)行工況,。由于其控制參數(shù)是在一定條件（如環(huán)境,、工況等）下設(shè)定的,，當(dāng)條件發(fā)生變化時(shí),，原整定參數(shù)不再適應(yīng)于當(dāng)前對(duì)象的動(dòng)態(tài)特性,，以至于使控制品質(zhì)下降,。而常規(guī)的PID控制的參數(shù)是根據(jù)調(diào)節(jié)對(duì)象的數(shù)學(xué)模型來進(jìn)行整定的，所以對(duì)于風(fēng)力發(fā)電試驗(yàn)系統(tǒng)電源組控制采用常規(guī)的PID控制器難以取得理想控制效果[1],。為了克服常規(guī)PID 控制存在的缺點(diǎn),，將神經(jīng)元自適應(yīng)PID控制器引入風(fēng)力發(fā)電試驗(yàn)系統(tǒng)電源組控制中,。

　　本文是基于湖南省科技計(jì)劃項(xiàng)目——風(fēng)力發(fā)電機(jī)智能綜合測(cè)控系統(tǒng)的研究，根據(jù)試驗(yàn)過程要求自動(dòng)實(shí)現(xiàn)試驗(yàn)電源組各單元的控制,，將神經(jīng)元自適應(yīng)PID控制用于電源組控制系統(tǒng)，以實(shí)現(xiàn)理想的控制效果,。將神經(jīng)元PID控制器的工程應(yīng)用與仿真研究相結(jié)合，在實(shí)現(xiàn)神經(jīng)元PID控制的優(yōu)良性能的基礎(chǔ)之上,，探索神經(jīng)元自適應(yīng)PID控制器參數(shù)的工程整定方法,。

　　1 風(fēng)力發(fā)電機(jī)試驗(yàn)系統(tǒng)電源組控制系統(tǒng)

　　圖1所示為風(fēng)力發(fā)電機(jī)試驗(yàn)系統(tǒng)電源組的控制系統(tǒng)結(jié)構(gòu)框圖,，系統(tǒng)是由神經(jīng)元自適應(yīng)PID控制器,、調(diào)節(jié)器、觸發(fā)器,、執(zhí)行機(jī)構(gòu)、濾波,、辨識(shí)環(huán)節(jié),、檢測(cè)電路、負(fù)載構(gòu)成的一個(gè)閉環(huán)控制回路,。

　　將給定信號(hào)（電壓、電流）的輸入值與負(fù)載電壓,、電流檢測(cè)反饋值進(jìn)行比較,為了消除給定輸入值與反饋值的誤差,將誤差送入神經(jīng)元自適應(yīng)控制器,，由調(diào)節(jié)器產(chǎn)生的控制信號(hào)根據(jù)一定的算法來進(jìn)行調(diào)整,發(fā)出電壓,、電流信號(hào)給執(zhí)行機(jī)構(gòu),，以實(shí)現(xiàn)電壓（轉(zhuǎn)速）及電流閉環(huán)控制,無差調(diào)節(jié),。在電源組內(nèi)部設(shè)置一個(gè)辨識(shí)環(huán)節(jié),，能有效辨識(shí)給定與輸出信號(hào)，從而實(shí)現(xiàn)輸出電流和輸出電壓（轉(zhuǎn)速）的穩(wěn)定[2],。因此，由外部電網(wǎng)和負(fù)載波動(dòng)等引起的電流變化,，均可通過快速調(diào)節(jié)輸出電壓而保持輸出電流的穩(wěn)定以及良好的調(diào)節(jié)性能,。充分利用神經(jīng)元自適應(yīng)PID控制的自學(xué)習(xí)和自適應(yīng)能力來克服負(fù)載的波動(dòng),，從而實(shí)現(xiàn)電源組穩(wěn)定、可靠地長(zhǎng)期運(yùn)行。

　　2 神經(jīng)元自適應(yīng)PID控制器設(shè)計(jì)

　　2.1 神經(jīng)元自適應(yīng)PID控制器的基本原理

　　在神經(jīng)網(wǎng)絡(luò)控制中,，單神經(jīng)元是最基本的控制單元,。神經(jīng)元PID 控制器具有現(xiàn)場(chǎng)整定參數(shù)簡(jiǎn)單,、便于現(xiàn)場(chǎng)調(diào)試的重要特點(diǎn), 能夠大大改善典型非線性時(shí)變對(duì)象的動(dòng)態(tài)性能, 能夠適應(yīng)過程的時(shí)變特性, 以保證控制系統(tǒng)在最佳狀態(tài)下運(yùn)行[3]。

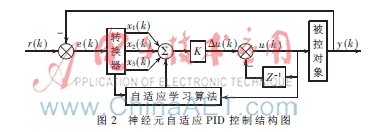
　　神經(jīng)元自適應(yīng)PID控制的結(jié)構(gòu)如圖2所示,。圖中轉(zhuǎn)換器的輸入反映被控過程及控制設(shè)定的狀態(tài),。設(shè)r(k)為設(shè)定值,，y(k)為輸出值，誤差e(k)經(jīng)轉(zhuǎn)換器轉(zhuǎn)換后成為神經(jīng)元的輸入量x1(k),、x2(k),、x3(k)。利用神經(jīng)元的在線調(diào)整功能,，把神經(jīng)網(wǎng)絡(luò)應(yīng)用于PID控制系統(tǒng)中,以改善常規(guī)PID的控制性能[4-5]。

　　其增量式表示為：

　　由式(1),、(2),、(3)可知神經(jīng)元控制器輸出的x1(k),、x2(k)、x3(k)即為PID調(diào)節(jié)器的比例,、積分,、微分輸入,，而w1、w2,、w3即為對(duì)應(yīng)的加權(quán)系數(shù)[6-7],。神經(jīng)元自適應(yīng)PID控制器通過某種學(xué)習(xí)算法不斷更新修改加權(quán)系數(shù),，從而實(shí)現(xiàn)自動(dòng)適應(yīng)被控對(duì)象的狀態(tài)環(huán)境變化的自學(xué)習(xí),、自適應(yīng)功能，所以神經(jīng)元PID控制器也可稱為在線自適應(yīng)PID控制器,。

　　2.2 自適應(yīng)控制規(guī)律

　　(1)一般神經(jīng)元PID控制規(guī)律

　　本文采用的一般神經(jīng)元自適應(yīng)PID控制的控制規(guī)律為：

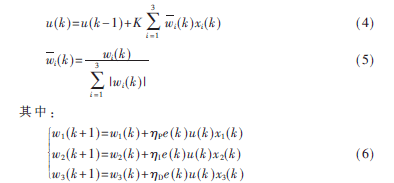
　　式(6)中,，K為神經(jīng)元比例系數(shù)，?濁P,、?濁I,、?濁D為比例,、積分、微分的學(xué)習(xí)效率,。對(duì)比例(P),、積分(I)、微分(D)分別采用不同的學(xué)習(xí)效率?濁P,、?濁I、?濁D,，以便對(duì)它們各自的權(quán)系數(shù)能根據(jù)需要分別進(jìn)行調(diào)整,。學(xué)習(xí)效率的取值可先由現(xiàn)場(chǎng)實(shí)驗(yàn)或仿真來確定。

　　(2)改進(jìn)的神經(jīng)元自適應(yīng)PID控制規(guī)律

　　神經(jīng)元PID參數(shù)的在線學(xué)習(xí)修正主要與 e(k),、?駐e(k)及神經(jīng)元比例系數(shù)K有關(guān),，因此可將神經(jīng)元自適應(yīng)PID控制算法中的加權(quán)系數(shù)學(xué)習(xí)修正部分及比例系數(shù)K進(jìn)行修改,，即將其中式(4)中的xi(k)改為e(k)+?駐e(k)，由式(4)可知神經(jīng)元的比例系數(shù)K為一常數(shù),，為了抑制較大擾動(dòng)量的影響(負(fù)載的突加與突卸時(shí)),，將K設(shè)定為一個(gè)隨e(k)和?駐e(k)變化的變量,，當(dāng)誤差較大時(shí)K值也較大,，當(dāng)誤差較小且接近穩(wěn)定時(shí)K值較小,，這時(shí)K值對(duì)系統(tǒng)的穩(wěn)定性影響較小。對(duì)上述控制規(guī)律稍加修改后的算法如下：

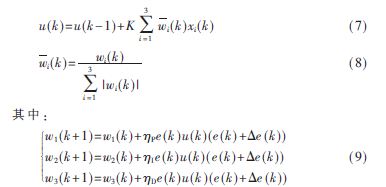
　　采用上述改進(jìn)的控制規(guī)律,，權(quán)系數(shù)的在線修正就不完全是根據(jù)神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)原理,，而是參考現(xiàn)場(chǎng)實(shí)際經(jīng)驗(yàn)來制定的。比例系數(shù)K不再是一個(gè)恒定值,，而是一個(gè)隨誤差變化的變量，有利于提高系統(tǒng)的穩(wěn)定性。

　　3 仿真分析

　　對(duì)于風(fēng)力發(fā)電機(jī)試驗(yàn)系統(tǒng)電源組的控制系統(tǒng),，其負(fù)載的種類很多,，有的結(jié)構(gòu)和工作過程相當(dāng)復(fù)雜，其內(nèi)部不止一個(gè)狀態(tài)變量,，要準(zhǔn)確描述其數(shù)學(xué)模型比較困難,，且階次很高,。但是在實(shí)際分析問題時(shí)，沒有必要用到特別復(fù)雜的高階次的數(shù)學(xué)模型,，而且通過仿真說明采用低階次的近似簡(jiǎn)單數(shù)學(xué)模型不僅實(shí)用,，且能得到比較滿意的仿真結(jié)果。因此本文選取的負(fù)載被控對(duì)象為二階系統(tǒng)

　　在對(duì)常規(guī)PID仿真中,，取常規(guī)PID參數(shù)為：Kp=0.10，Ki=0.01,，Kd=0.10，采樣時(shí)間Ts=1 ms,。在對(duì)一般神經(jīng)元自適應(yīng)PID仿真中,，取學(xué)習(xí)效率?濁p=0.40,，?濁i=0.35,，?濁d=0.40，K=0.052,，采樣時(shí)間Ts同為1 ms,。采用一般神經(jīng)元自適應(yīng)PID控制與常規(guī)PID控制算法仿真對(duì)比結(jié)果如圖3所示，誤差跟蹤曲線對(duì)比如圖4所示,。

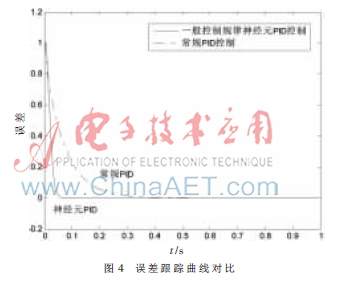
　　由圖3,、圖4可知，神經(jīng)元自適應(yīng)PID控制器的控制性能要優(yōu)于常規(guī)PID控制器,，能夠?qū)?shù)在線自適應(yīng)調(diào)整以實(shí)現(xiàn)良好的控制效果,，較常規(guī)PID控制器的快速性、穩(wěn)定性好,，且沒有超調(diào),，可以達(dá)到理想的控制效果,。而采用改進(jìn)控制規(guī)律的神經(jīng)元自適應(yīng)PID控制根據(jù)實(shí)際情況，取a=0.12,、?琢=0.2、?茁=0.3,，其余參數(shù)保持不變,，其與常規(guī)PID控制算法仿真對(duì)比結(jié)果如圖5所示，圖6所示為其誤差曲線比較,。

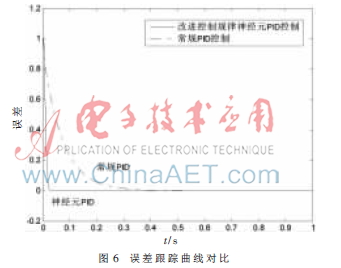
　　由圖5,、圖6可以看出，改進(jìn)控制規(guī)律的神經(jīng)元自適應(yīng)PID控制要優(yōu)于一般的神經(jīng)元PID控制,，其快速性更好,，可以使系統(tǒng)更快地趨于穩(wěn)定，減少了系統(tǒng)的誤差,，具有良好的控制性能,。在不同情況下，試驗(yàn)系統(tǒng)的電源組需要帶不同的負(fù)載,，其傳遞機(jī)構(gòu)的傳遞函數(shù)或者負(fù)載主電路發(fā)生變化時(shí),，只要改變?cè)鲆鍷的初始值以及對(duì)應(yīng)于誤差的權(quán)值?琢、?茁就可以獲得理想的效果,，較一般的神經(jīng)元PID控制器與常規(guī)PID控制器調(diào)節(jié)起來更加方便實(shí)用,。

　　仿真結(jié)果表明：常規(guī)PID控制效果雖然具有調(diào)節(jié)方便、結(jié)構(gòu)簡(jiǎn)單等優(yōu)點(diǎn),，但是其控制難以達(dá)到理想的效果,，尤其是當(dāng)對(duì)象為非線性時(shí)，通常會(huì)出現(xiàn)調(diào)節(jié)時(shí)間過長(zhǎng)的弱點(diǎn),；而神經(jīng)元自適應(yīng)PID控制具有優(yōu)于常規(guī)PID控制的控制效果,。

　　本文提出的神經(jīng)元自適應(yīng)PID控制器具有結(jié)構(gòu)簡(jiǎn)單、控制算法簡(jiǎn)單易懂,、實(shí)現(xiàn)方便等特點(diǎn),，既保持了常規(guī)PID控制的優(yōu)點(diǎn)，又有很強(qiáng)的自學(xué)習(xí)智能特性,，將其應(yīng)用于風(fēng)力發(fā)電機(jī)試驗(yàn)系統(tǒng)電源組的控制系統(tǒng)中,，以其良好的自適應(yīng)性，可以自學(xué)習(xí)地對(duì)PID參數(shù)進(jìn)行實(shí)時(shí)調(diào)整,。試驗(yàn)過程實(shí)現(xiàn)了對(duì)系統(tǒng)各單元的自動(dòng)控制,，達(dá)到了節(jié)能最佳的目的，電源的波形及各項(xiàng)指標(biāo)符合國(guó)家標(biāo)準(zhǔn),，達(dá)到了理想的控制效果,。

　　參考文獻(xiàn)

　　[1] 李作軍.基于DSP的變頻電源數(shù)字化控制技術(shù)的研究[D].武漢：武漢理工大學(xué),，2008.

　　[2] 李小英，匡宇國(guó).模糊自適應(yīng)整定PID-FS在整流電源中的應(yīng)用[J].電力電子技術(shù),，2007,，41(2)：63-65.

　　[3] LIN W M，HONG C M.Fuzzy neural network output maximization control for sensorless wind energy conversion system[J].Energy,，2010,，35(2)：592-601．

　　[4] 王迎旭，沈?qū)W軍.神經(jīng)元自適應(yīng)PID控制器在機(jī)組控制中的應(yīng)用[J].控制工程,，2004,，11(2)：206-208.

　　[5] 張學(xué)燕.神經(jīng)網(wǎng)絡(luò)自適應(yīng)PID控制器的研究與仿真[D].貴陽(yáng)：貴州大學(xué)，2008.

　　[6] 劉金琨.先進(jìn)PID控制MATLAB仿真[M].北京：電子工業(yè)出版社,，2004.

　　[7] 王迎旭,，劉國(guó)繁，伍萍輝.基于神經(jīng)網(wǎng)絡(luò)的自適應(yīng)PID控制器及其應(yīng)用[J].電力電子技術(shù),，2004,，38(2)：89-91.