摘  要： 無線傳感器網(wǎng)絡(luò)通過少數(shù)確定錨節(jié)點(diǎn)計(jì)算到其他節(jié)點(diǎn)距離，確定節(jié)點(diǎn)坐標(biāo),。其中DV-Hop定位算法通過最小二乘法求解坐標(biāo),，累計(jì)誤差隨節(jié)點(diǎn)平均距離誤差呈指數(shù)增長(zhǎng)，定位精度較低,。提出了用粒子群PSO離散算法替代DV-Hop中的最小二乘法, 既發(fā)揮PSO全局搜索能力,，又避免標(biāo)準(zhǔn)PSO算法過早收斂的問題。實(shí)驗(yàn)結(jié)果表明,，新算法定位精度很高,，受距離誤差影響不大，能很好地應(yīng)用于無線傳感器網(wǎng)絡(luò)的定位過程,。

　　關(guān)鍵詞： 無線傳感器網(wǎng)絡(luò),；粒子群；DV-Hop定位算法,；離散算法

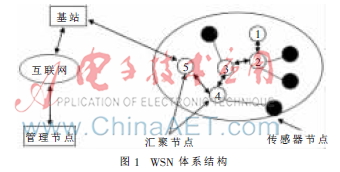
　　無線傳感器網(wǎng)絡(luò)WSN(Wireless Sensor Networks)由大量傳感節(jié)點(diǎn)以多跳自組織方式構(gòu)成,，通過數(shù)據(jù)采集,、協(xié)調(diào)感知完成信息搜集和管理任務(wù),。無線傳感器網(wǎng)絡(luò)一般應(yīng)用于惡劣環(huán)境或是人無法抵達(dá)區(qū)域，受鋪設(shè)成本和能源供給限制,，只有少數(shù)匯聚節(jié)點(diǎn)配備GPS定位裝置,，通過與網(wǎng)絡(luò)其他傳感器節(jié)點(diǎn)接力通信完成對(duì)其定位過程,。典型的WSN由傳感器節(jié)點(diǎn)、匯聚節(jié)點(diǎn)和管理節(jié)點(diǎn)組成,，如圖1所示,。傳感器節(jié)點(diǎn)感知目標(biāo)信息后以多跳接力方式傳給匯聚節(jié)點(diǎn)，匯聚節(jié)點(diǎn)對(duì)附近傳感器節(jié)點(diǎn)信息匯總后通過衛(wèi)星基站,、互聯(lián)網(wǎng)傳送給管理用戶[1],。由于傳感器節(jié)點(diǎn)一般可移動(dòng)部署以適應(yīng)環(huán)境變化，如何精確定位傳感器節(jié)點(diǎn)坐標(biāo)成為WSN研究的熱點(diǎn)和難點(diǎn),。

　　1 WSN定位算法分類

　　無線傳感器網(wǎng)絡(luò)節(jié)點(diǎn)定位算法分為基于測(cè)距和無需測(cè)距算法兩類[2],。對(duì)于大部分傳感節(jié)點(diǎn)而言，當(dāng)定位誤差小于節(jié)點(diǎn)通信半徑的40%時(shí),，定位誤差對(duì)節(jié)點(diǎn)精確度的影響不大[2],。若使用測(cè)距定位不僅要配備額外硬件設(shè)備，增加節(jié)點(diǎn)成本,，還會(huì)加重電源補(bǔ)給負(fù)荷,。無需測(cè)距算法通過節(jié)點(diǎn)之間通信估算彼此之間距離、定位節(jié)點(diǎn)坐標(biāo),，簡(jiǎn)單方便,，得到廣泛應(yīng)用。其中最為經(jīng)典的是DV-Hop算法,。

　　2 DV-Hop算法

　　DV-Hop稱為距離向量跳段定位算法,，用網(wǎng)絡(luò)平均跳距和節(jié)點(diǎn)間最短跳數(shù)乘積表示節(jié)點(diǎn)之間距離，再利用大量冗余信息節(jié)點(diǎn)實(shí)現(xiàn)定位,。整個(gè)過程分為3個(gè)階段：

　　(1)計(jì)算抵達(dá)鄰居節(jié)點(diǎn)跳數(shù),。傳感節(jié)點(diǎn)定期向鄰居節(jié)點(diǎn)交換抵達(dá)網(wǎng)絡(luò)中其他節(jié)點(diǎn)距離，以跳數(shù)為單位,。最終每個(gè)傳感節(jié)點(diǎn){xi,，yi}都獲得自身參考節(jié)點(diǎn)跳數(shù)hi及參考坐標(biāo){xi，yi,，hi},。

　　(2)每個(gè)傳感節(jié)點(diǎn)使用式(1)計(jì)算到達(dá)其他參考節(jié)點(diǎn)的距離。

　　(3)傳感節(jié)點(diǎn)得到與其他參考節(jié)點(diǎn)距離后,，通過三角或多邊測(cè)量建立方程組,，最后利用最小二乘法求解方程組獲得節(jié)點(diǎn)坐標(biāo)。

　　DV-Hop實(shí)現(xiàn)簡(jiǎn)單,、方便快捷,，但算法中的距離通過節(jié)點(diǎn)跳數(shù)乘以網(wǎng)絡(luò)平均跳距得出[3]，不可避免地存在誤差,，加上最小二乘法求解精度依賴于網(wǎng)絡(luò)跳距初始參數(shù),，導(dǎo)致產(chǎn)生的誤差呈指數(shù)增長(zhǎng),、定位精度不高，并且節(jié)點(diǎn)密度越低,，拓?fù)湓讲灰?guī)則,，誤差越大。

　　3 基于粒子群定位算法思想

　　傳感節(jié)點(diǎn)記為P1(x1,，y1),，P2(x2，y2),，…,，Pn(xn，yn),，根據(jù)DV-Hop前兩階段估算的抵達(dá)網(wǎng)絡(luò)其他節(jié)點(diǎn)距離分別是d1,，d2…，dn,，估算距離與真實(shí)距離之間差值分別為ε1,，ε2，…,，εn,，得以下方程組：

　　傳感節(jié)點(diǎn)坐標(biāo)應(yīng)同時(shí)滿足式(2)方程組要求，若|ε1|+|ε2|+…+|εn|和越小,，則節(jié)點(diǎn)坐標(biāo)越優(yōu),、定位越精確，從而可利用最小二乘法求解過程轉(zhuǎn)換為使用粒子群算法求解全局最小最優(yōu)解的問題,，如式(3)所示,。

　　本文提出將粒子群(PSO)離散算法替代DV-Hop中的最小二乘法，用于求解節(jié)點(diǎn)最優(yōu)坐標(biāo),，既可以發(fā)揮PSO全局搜索能力,，又可以避免標(biāo)準(zhǔn)PSO算法中過早收斂問題，由此減小網(wǎng)絡(luò)跳距誤差對(duì)定位精度的影響范圍,。

　　4 標(biāo)準(zhǔn)粒子群算法

　　粒子群算法是基于鳥類群體行為研究的模擬算法,。鳥群在封閉空間隨機(jī)搜索食物，并且在這個(gè)空間只有一個(gè)全局最優(yōu)值[4],。假如所有鳥只都知道當(dāng)前位置與搜索食物之間的距離,，那么找到全局最優(yōu)解的最優(yōu)方案就是從身邊最近的鳥周圍區(qū)域進(jìn)行搜尋[5]。在粒子群算法中,，尋找最優(yōu)問題的每個(gè)解對(duì)應(yīng)搜索空間的每只鳥,，稱為粒子。每個(gè)粒子的初始化向量代表鳥的飛行位置和速率，每個(gè)粒子通過尋找附近粒子迭代搜尋最優(yōu)解,，具體算法如下：

　　假設(shè)在一個(gè)d維搜索空間中，有n個(gè)粒子組成的粒子群X=(X1,，X2,，…，Xn)T,，其中第i個(gè)粒子位置為Xi=(Xi1,，Xi2，…,，XiD)T,，速率為Vi=(Vi1，Vi2,，…,，Vid)T，極值為Pi=(Pi1,，Pi2,，…，Pid)T,，種群全局極值為Pg=(Pg1,，Pg2，…,，Pgd)T,，每個(gè)粒子找到下一粒子后按以下公式更新當(dāng)前位置和速率[6]：

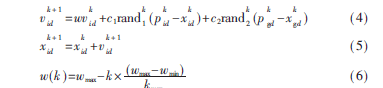
　　其中，k表示迭代次數(shù),，c1,、c2為加速系數(shù)，rand是[0,，1]區(qū)間選取的隨機(jī)數(shù),，p是第i個(gè)粒子的個(gè)體極值在第d維的分量，p是群體全局極值在第d維的分量,，x,、v分別是第i個(gè)粒子經(jīng)k次迭代后的第d維位置和速率，w是粒子保持運(yùn)動(dòng)慣性權(quán)重,。粒子通過不斷更新當(dāng)前位置和速率最終找到全局最優(yōu)解,，完成搜索過程。

　　5 新算法定位模型

　　5.1 離散粒子群算法

　　粒子群算法前期收斂速率快,，但容易出現(xiàn)前期局部最優(yōu),、后期收斂緩慢的問題。改進(jìn)離散粒子群算法在于更新粒子當(dāng)前位置和速率前引入離散運(yùn)動(dòng)方程式：

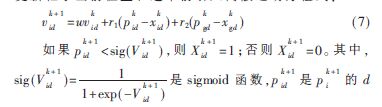
　　d維分量。粒子的位置只有“0”,、“1”兩種狀態(tài),，速率越小，粒子取“0”幾率越大,，反之取“1”,。改進(jìn)離散粒子群算法使得函數(shù)sig(V)不會(huì)過于接近“0”或“1”，保證算法以一定概率從一種狀態(tài)躍遷到另一種狀態(tài),，從而避免算法過早收斂,，出現(xiàn)局部最優(yōu)現(xiàn)象。

　　5.2 新算法適應(yīng)度值選擇

　　新算法通過估計(jì)的距離與真實(shí)距離之間的差值ε1+ε2+…+εn之和判斷粒子所處位置優(yōu)劣,，以此確定是否符合全局最優(yōu)解要求,。差值之和越小，適應(yīng)度值越大,。求解適應(yīng)度公式為：

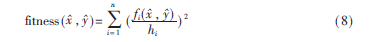
　　其中,，n為傳感節(jié)點(diǎn)數(shù)量；hi為傳感節(jié)點(diǎn)抵達(dá)網(wǎng)絡(luò)其他節(jié)點(diǎn)跳數(shù),，由DV-Hop算法第一階段獲得,。由于傳感節(jié)點(diǎn)跳數(shù)越多，誤差累積越大,，因此在計(jì)算適應(yīng)度時(shí)加入權(quán)重,，hi越大的傳感節(jié)點(diǎn)對(duì)適應(yīng)值影響越小。

　　5.3 新算法粒子聚集度

　　在標(biāo)準(zhǔn)PSO算法中,，兩個(gè)粒子之間的距離表示其相似程度大小,，距離越近相似度越高。新算法用s(i,，j)表示粒子i和粒子j之間的相似度,，滿足以下條件：

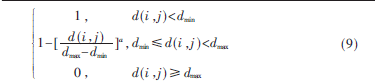
　　其中，d(i,，j)為粒子i和粒子j之間的距離,，dmin、dmax表示所有粒子之間距離的最小值和最大值,。隨著迭代次數(shù)增多,，粒子適應(yīng)度越大，與最優(yōu)粒子相似度越高,，位置越趨于全局最優(yōu)解,，最終聚集在一起。新算法聚集度為：

　　其中,，C(t)是粒子群經(jīng)t次迭代的聚集度,，m為種群規(guī)模,。種群聚集度最密的粒子群收斂于當(dāng)前全局最優(yōu)解。

　　5.4 新算法定位流程

　　新算法采用改進(jìn)PSO離散算法替代DV-Hop算法中第3階段的最小二乘法,，利用離散PSO迭代求解避免網(wǎng)絡(luò)跳距誤差對(duì)定位精度帶來的影響,，并得到3個(gè)全局體極值的幾何質(zhì)心解，最后計(jì)算傳感節(jié)點(diǎn)坐標(biāo),。具體步驟如下,。

　　(1)基于DV-Hop算法第1階段和第2階段，傳感節(jié)點(diǎn)間通過與鄰居節(jié)點(diǎn)通信獲得自身參考坐標(biāo){xi,，yi，hi},，并計(jì)算抵達(dá)網(wǎng)絡(luò)其他節(jié)點(diǎn)距離,。

　　(2)根據(jù)網(wǎng)絡(luò)節(jié)點(diǎn)規(guī)模和區(qū)域大小初始化種群，計(jì)算每個(gè)粒子適應(yīng)度,，每個(gè)粒子位置都是節(jié)點(diǎn)定位坐標(biāo)的可行解,。

　　(3)根據(jù)適應(yīng)度大小更新粒子個(gè)體極值，同時(shí)找出全局適應(yīng)度最好的3個(gè)個(gè)體極值保存在近優(yōu)解集合中,。

　　(4)根據(jù)粒子速率利用離散運(yùn)動(dòng)方程式(7)對(duì)粒子群狀態(tài)進(jìn)行躍遷,，避免算法過早收斂。

　　(5)根據(jù)式(4)重新計(jì)算粒子當(dāng)前位置和速率,。

　　(6)根據(jù)式(9)計(jì)算每個(gè)粒子與全局近優(yōu)解相似度,，并根據(jù)式(10)計(jì)算當(dāng)前迭代種群的聚集度。

　　(7)判斷是否滿足結(jié)束條件（達(dá)到最大迭代次數(shù)或保存近優(yōu)數(shù)組中的3個(gè)個(gè)體極值都達(dá)到最優(yōu)要求),，結(jié)束迭代循環(huán),，獲得3個(gè)全局體極值坐標(biāo)，否則跳到步驟(3),。

　　(8)通過極值幾何質(zhì)心坐標(biāo)計(jì)算定位傳感節(jié)點(diǎn)位置,。

　　6 仿真測(cè)試

　　6.1 仿真環(huán)境

　　仿真環(huán)境設(shè)為100 m×100 m二維區(qū)域，節(jié)點(diǎn)通信半徑為20 m,，傳感節(jié)點(diǎn)比例為80%,，初始化粒子群規(guī)模200，最大迭代次數(shù)500,，慣性權(quán)重Wmax=0.9,，Wmin=0.4，平均定位誤差評(píng)價(jià)為：

　　6.2 定位誤差分析

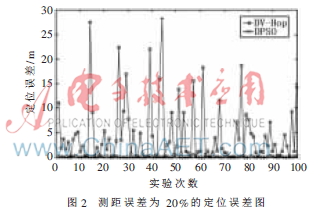
　　新算法用PSO離散（DPSO）算法替代DV-Hop中的最小二乘法以計(jì)算節(jié)點(diǎn)坐標(biāo),，減小DV-Hop網(wǎng)絡(luò)跳距誤差對(duì)定位精度的影響,。在相同網(wǎng)絡(luò)環(huán)境下，新算法在測(cè)距誤差為 20%的定位誤差明顯小于DV-Hop算法,，如圖2所示,。

　　6.3 標(biāo)準(zhǔn)偏差分析

　　在測(cè)距誤差逐漸增加時(shí),，開始兩種算法定位標(biāo)準(zhǔn)偏差都有所增長(zhǎng)，但新算法相比DV-Hop中的標(biāo)準(zhǔn)偏差增長(zhǎng)更為緩慢,，如圖3所示,。因?yàn)樾滤惴ㄕ`差增長(zhǎng)受節(jié)點(diǎn)平均距離誤差影響，而DV-Hop算法誤差激增是由于最小二乘法對(duì)節(jié)點(diǎn)平均距離誤差放大的結(jié)果,。當(dāng)新算法測(cè)距誤差增長(zhǎng)到10%時(shí),，標(biāo)準(zhǔn)偏差開始降低，這是由于在計(jì)算適應(yīng)度時(shí)加入權(quán)重,，hi越大的傳感節(jié)點(diǎn)對(duì)適應(yīng)值影響越小,，節(jié)點(diǎn)平均距離誤差隨節(jié)點(diǎn)距離增長(zhǎng)影響越弱，最大測(cè)距標(biāo)準(zhǔn)偏差收斂于2 m以內(nèi),，可見新算法在定位平均測(cè)距誤差較大的情況下更具優(yōu)勢(shì),。

　　6.4 收斂性分析

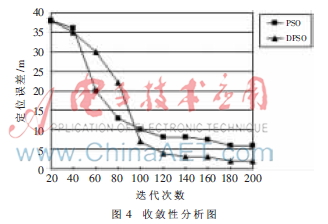
　　與標(biāo)準(zhǔn)PSO算法相比，兩種算法定位誤差都隨迭代次數(shù)增多而減小,，如圖4所示,。在迭代次數(shù)較少時(shí)兩種算法誤差較大，這是因?yàn)榱Ｗ尤撼跏蓟^程中粒子分布隨機(jī)性造成的,。標(biāo)準(zhǔn)PSO算法在迭代次數(shù)達(dá)到100時(shí),，曲線趨于平穩(wěn)，定位誤差起伏不大,，算法開始收斂,，但定位誤差明顯大于新算法，由此推斷算法過早收斂陷入局部最優(yōu)解,。而新算法在迭代次數(shù)達(dá)到120時(shí),，定位誤差才接近最優(yōu)解，最終定位誤差收斂于2 m以內(nèi),，這與圖3實(shí)驗(yàn)數(shù)據(jù)一致,。

　　本文采用粒子群離散算法替代DV-Hop算法中的最小二乘法，避免網(wǎng)絡(luò)跳距估計(jì)誤差對(duì)定位精度帶來的影響,。接下來的工作將著眼于減少算法復(fù)雜度,，降低無線傳感網(wǎng)絡(luò)能耗問題，以減少實(shí)際部署中對(duì)環(huán)境的依賴程度,。

　　參考文獻(xiàn)

　　[1] NICULESCU D.Localized positioning in ad-hoc networks[J].IEEE International Workshop on Sensor Network Protocols and Applications,，2003，1(2)：42-50.

　　[2] PATWARI N.Relative location estimation in wireless sensor networks[J].IEEE Transactions on Signal Processing,，2003,，51(8)：2137-2148.

　　[3] RANDOLPH.A self-localization method for wireless sensor networks[J].EURASIP Journal on Applied Signal Processing，2003(4)：348-358.

　　[4] LANGENDOEN K.Distributed localization in wireless sensornetworks[J].Computer Networks.2003,，43(4)：499-518.

　　[5] GUSTAFSSON F.Mobile positioning using wireless networks[J].IEEE Signal Processing Magazine,，2005,，22(4)：41-53.

　　[6] YEDAVALLI K.Sequence-based localization in wireless sensor networks[J].IEEE Transactions on Mobile Computing，2008,，7(1)：81-94.