摘 要: 針對稱重儀表檢測電路中輸入與輸出值之間存在非線性關系的特性,在比較了幾種非線性校正方法的基礎上,給出了一種易于微處理器實現(xiàn)的正交多項式的非線性校正方法,求取稱重儀表檢測電路的非線性特征,實現(xiàn)了稱重儀表的非線性校正。同時討論了該算法的原理、校正參數(shù)的空間復雜度和算法的時間復雜度,從而論證了此算法在簡單微處理器上的可用性,并以3階多項式為例介紹了該算法的實驗效果。實踐表明,該算法簡單實用,效果較好。
關鍵詞: 正交多項式;傳感器;非線性校正
稱重儀表是電子衡器的心臟部件,它融合了當今先進的信息技術和計算機技術,在工業(yè)過程控制和貿(mào)易結算等方面得到了廣泛應用。隨著微型計算機技術和嵌入式系統(tǒng)的迅速發(fā)展,現(xiàn)代測控系統(tǒng)對稱重儀表準確度、穩(wěn)定性和工作條件等方面提出了更高的要求。然而,由于電子元器件性能參數(shù)的離散性、穩(wěn)定性和敏感性等因素的影響,使得壓力傳感器的反饋信號X和被測物體的質(zhì)量Y不是標準的線性關系。因此,需要對稱重儀表增加非線性校正環(huán)節(jié)。
非線性校正可以通過模擬電路來實現(xiàn),但是模擬電路的接入不但增大了儀表的體積和成本,而且還會帶來新的非線性因素。隨著智能化儀表的發(fā)展,軟件非線性校正方法得到了廣泛應用。目前,非線性校正方法主要有遺傳算法[1]、神經(jīng)網(wǎng)絡法[2]、支持向量機法[3]、插值法[4]、函數(shù)擬合法等,這些方法取得了良好的校正效果,但是由于算法的復雜性對稱重儀表的處理器速度和存儲器容量提出更高要求,使得其中一些算法在普通的智能儀表中實現(xiàn)困難。鑒于這個原因,參考文獻[5]和參考文獻[6]分別采用了分段插值法和最小二乘法擬合曲線函數(shù)達到了較好的效果。然而分段插值法雖然算法簡單,但是需要保存的浮點數(shù)參數(shù)隨著插值節(jié)點的增加而增多,對于存儲空間有限的稱重儀表來說浪費了過多的資源;最小二乘法擬合曲線函數(shù)雖然算法成熟,需保存的參數(shù)也不多,但是在工程實踐中經(jīng)常會出現(xiàn)參數(shù)差異較大的病態(tài)方程,使得出的數(shù)據(jù)不可靠。本文基于正交多項式構造了一個稱重儀表的非線性校正系統(tǒng),既降低了曲線擬合算法的運算復雜度,又節(jié)省了存儲空間,提高了稱重儀表的可靠性和穩(wěn)定性。
1 稱重儀表的非線性校正原理

如圖1所示,稱重儀表由稱重壓力傳感器、放大電路、濾波器、采樣保持器、A/D轉換電路、微處理器及相關附屬配件組成。其中,微處理器和A/D轉換電路是稱重儀表的核心部件,負責將壓力傳感器反饋的模擬量轉換為數(shù)字量,同時,依據(jù)計量算法將此數(shù)字量轉換成稱重物體的稱重值。
軟件實現(xiàn)稱重儀表的非線性校正就是在測量系統(tǒng)中為被測物重量與電信號輸出之間構造理想的非線性函數(shù)關系。假設被測物體的質(zhì)量為m,傳感器及其采集電路的電信號輸出為v,其校正模型表示為v=g(m)。在A/D轉換之后增加一個由微處理器實現(xiàn)的非線性校正環(huán)節(jié)y=f(v),使補償后的輸出y與被測質(zhì)量u之間具有良好的線性特征,即:
Y=u=g-1(m)(1)
由式(1)可知,當非線性校正環(huán)節(jié)為稱重儀表的反函數(shù)時,則可實現(xiàn)稱重儀表輸出的非線性校正。由于g(m)函數(shù)具有高度的非線性,因此f(v)很難直接獲得。本文利用正交多項式構造了稱重儀表的擬合函數(shù),實現(xiàn)了稱重儀表的非線性校正。
2 正交多項式的非線性校正原理
稱重儀表的非線性特征可以用m次多項式的非線性曲線來逼近,該多項式方程通過構造正交多項式[7]來獲得。對于稱重儀表通過靜態(tài)實驗標定獲得的數(shù)據(jù)點(xi,yi)(i=1,2,…,n),此處x為稱重儀表通過A/D轉換后獲得的數(shù)字量,y為稱重值,選取一組在這些點上的正交的多項式函數(shù)系{Qi(xi),j=0,1,…,m}作為基函數(shù)組,其中Qi(xi)是j次多項式。擬合多項式記為:

式(4)中,k,j=0,1,…,m,一般m遠小于n。
根據(jù)格拉姆-施密特正交化方法,構造給定點上的正交多項式Qj(x)(j=0,1,…,m-1)的方法如下:
Q0(x)=1Q1(x)=(x-?琢0)Qj+1(x)=(x-?琢j)Qj(x)-?茁jQj-1(x)(5)
其中:

通過以上遞推公式,可以將式(2)推導為m次多項式的一般形式:

將q0Q0(x)項展開后累加到式(7),得:
當j=1時,令Q1(x)=t0+t1x,顯然,t0=0,t1=1。由遞推公式(3)得:

將q1Q1(x)項展開后累加到多項式(7)中,即有:
a0+q1t0?圯a0
q1t1?圯a1
對于j=2,3,…,m,逐步遞推Qj(x),根據(jù)式(5)有:

3 算法設計
3.1 校正方程參數(shù)的數(shù)據(jù)結構和空間復雜度
由式(7)可知,m階正交多項式的非線性校正方程常駐內(nèi)存參數(shù)由m+1個多項式系數(shù)組成,即a0,a1,…,am,在算法中將這些參數(shù)定義為一個數(shù)組a[0],a[1],…,a[m]。在稱重儀表稱重過程中實時用到這些參數(shù)進行非線性校正。如果使用3階正交多項式,只需要4個浮點數(shù),一般的微處理器完全可以支持。
由式(14)可以看到,m階多項式系數(shù)的計算過程中還需要3個長度為m+1的數(shù)組(即公式中的s、t、b)作為臨時輔助變量,在算法中,分別定義為s[m]、t[m]、 b[m],其中m=0,1,…,m,共需3×(m+1)個浮點數(shù)。此外,通過算法優(yōu)化,可以將式(3)和式(6)中的3個長度為m+1的參數(shù)值(即公式中的α、β、q)縮減為3個變量重復使用,在算法中定義為α、β、q三個浮點數(shù)。
同時,由遞推公式(3)和(6),n個數(shù)據(jù)采樣點也要占用2n個浮點數(shù)分別存放采樣值x和稱重值y作為臨時變量。在算法中定義為長度為n的數(shù)組x[n]、y[n]。
綜上所述,構造n個采樣點的m階正交多項式所需臨時變量的空間復雜度為:
2n+3(m+1)+(m+1)+3
由此計算,如果構造10個采樣點的3階正交多項式,構造過程共需39個浮點數(shù),其中,臨時變量35個,常駐內(nèi)存變量4個。如果微處理器的存儲內(nèi)存資源不能達到要求,可以用離線方式構造正交多項式,只將多項式系數(shù)保存在稱重儀表中在線使用。
3.2 正交多項式校正算法流程和時間復雜度
以下給出m階正交多項式算法流程,其中m≥3。
算法預備:通過稱重儀表靜態(tài)標定,獲取n個采樣點(xi,yi)分別存入數(shù)組x[n]、y[n],并定義其他上述相關變量。
(1)當j=0時,依據(jù)式(8)求取式(2)中的q0,并且將q0的值放入多項式系數(shù)a[0]中保存,依據(jù)式(9)計算α0并保存到α中,令b[0]=1。
(2)當j=1時,t[0]=-α0,t[1]=1。依據(jù)式(10)~式(12)計算式(2)和式(5)的α1、β1、q1并分別保存到變量α、β、q中。同時,更新多項式系數(shù)a[0]=a[0]-α×q,a[1]=q。
(3)當j=2,3,…,m時,依據(jù)式(14)和式(15)依次進行以下運算和變量更新:
①s[j]=t[j-1];
②s[j-1]=-α×t[j-1]+t[j-2];
③當j≥3時,依次對k=j-2,j-3,…,1進行如下運算:
s[k]=α×t[k]+t[k-1]-β×b[k];
④s[0]=-α×t[0]-β×b[0];
⑤當k=j-1,j-2,…,0時,由式(3)、式(6)計算當前的αj、βj、qj并分別保存到變量α、β、q中,在下一次循環(huán)中使用;
⑥當k=j-1,j-2,…,0時,更新如下變量:b[k]=t[k]; t[k]=s[k];
⑦由式(15),更新多項式系數(shù)a[j]=q×s[j];
⑧由式(15),更新當k=j-1,j-2,…,0時多項式系數(shù)a[k]=q×s[k]+a[k]。
(4)保存正交多項式系數(shù)a[0],a[1],…,a[m]。
可以看出,構造正交多項式的時間復雜度主要集中在步驟(3)。其中,計算①、②、③中s[j]的累計時間復雜度為(m+2)(m-1)/2,⑥、⑦、⑧的計算可放在同一循環(huán)中,其時間復雜度為(m+2)(m-1)/2。除此之外,計算⑤中αj、βj、qj還需要n(m+2)(m-1)/2次的運算。總的時間復雜度為:
(n+1)(m+2)(m-1)/2
當用10個采樣點構造3階正交多項式時,其時間復雜度為55,這個值對于一般的微處理器來說完全可以支持。
4 實驗結果分析
4.1 實驗方案
為了檢驗正交多項式對稱重儀表輸入電壓值u和重量值x的實際逼近效果,實驗分兩步進行:
(1)選取0~380 kg作為稱重儀表的量程,每隔40 kg測量一次,一共獲得10個數(shù)據(jù)作為數(shù)據(jù)標定點(xi,ui),結果如表1所示。用這10個采樣點構造3階正交多項式,獲得多項式系數(shù)。
(2)以20 kg為間隔,在0~380 kg之間測量電壓值作為測試點,共獲得20個測試點并代入正交多項式進行檢驗(結果如表2所示)。
最后計算所有測試點的相對誤差,分析實驗結果。
4.2 實驗結果

由表1所列的數(shù)據(jù)標定點,按照正交多項式構建方法求得正交多項式系數(shù)為:a0=12.8278,a1=1.2659,a2= -4.3691×10-5,a3=-2.8491×10-8,從而求得此稱重儀表非線性校正環(huán)節(jié)的表達式為:
w(u)=-12.8278+1.2659u-4.3691×10-5u2-2.8491×10-8u3(16)
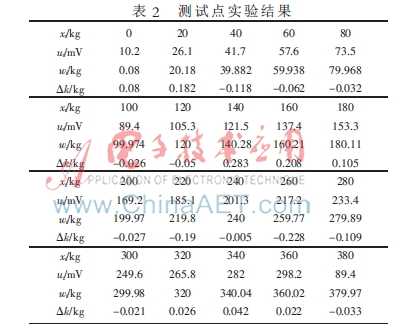
將表2中的20個測試值ui代入式(16),求得實際測量值wi,從表2可以看出,最大誤差為0.283,最小誤差為-0.005,誤差的算術平均值為0.003。

圖2是根據(jù)相對誤差計算公式式(17)繪制的各稱重測試點相對誤差直方圖。從圖中可以看出,所有試驗點的相對誤差均未超過1%,19個相對誤差測試點中,相對誤差最大的是稱重載荷最小的點,其相對誤差是 0.9%,其次是第二個測試點,相對誤差是0.3%,其他測試點的相對誤差逐漸減小,最大不超過0.2%,平均相對誤差0.03%,當稱重載荷大于300 kg時相對誤差小于 0.01%,其精度完全符合測試要求。從相對誤差的變化趨勢上看,當稱重載荷質(zhì)量較小時,相對誤差較大;稱重載荷越大,相對誤差呈鋸齒狀減小。這說明正交多項式與稱重儀表的實際值很接近,誤差值很平均,稱重越重,相對誤差就越小。因此,在精度要求較高時,正交多項式校正算法更適用于接近滿量程的應用。
δ=?駐k/xi×100%(17)
本文針對稱重儀表采集信號輸入和稱重值輸出呈非線性特征,在稱重系統(tǒng)中加入了由軟件方法實現(xiàn)的非線性校正環(huán)節(jié),利用正交多項式擬合法進行了非線性補償。實驗結果表明,稱重儀表通過非線性校正之后最大相對誤差小于1%,稱重越大,相對誤差越小,其校正效果能達到實際需要。
實際應用中也表明,正交多項式非線性校正技術算法簡單可靠、運算過程中所需存儲器容量較小,易于在只配備簡單微處理器的稱重儀表中實現(xiàn)。在實際應用中提高了稱重計量準確性和靈敏度,降低了誤差,具有廣泛的應用價值。
參考文獻
[1] 范鎧.傳感器軟件非線性校正方法綜述[J].上海計量測試,2004,31(2):8-12.
[2] 陳俊杰,蘆俊,黃惟一.基于遺傳神經(jīng)網(wǎng)絡的傳感器系統(tǒng)的非線性校正[J].儀器儀表學報,2003,24(2):201-204.
[3] 劉濤,王華.傳感器非線性校正的遺傳支持向量機方法[J].電子測量與儀器學報,2011,25(1):56-60.
[4] 劉少強,黃惟一.基于插值計算與優(yōu)化的鉑電阻非線性校正方法[J].儀器儀表學報,2003,24(2):215-217.
[5] 文其知,戴永.智能儀表非線性自動校正方法研究[J].自動化儀表,2009,30(6):75-78.
[6] 魏國,王昕,雷苗,等.基于B樣條遞推最小二乘的溫度傳感器非線性校正[J].傳感器與微系統(tǒng),2008,27(12):54-56.
[7] 徐士良.計算方法[M].北京:人民郵電出版社,2009.

