摘 要: 為了提高刀具預(yù)調(diào)測(cè)量?jī)x的檢測(cè)精度,提出了一種改進(jìn)的圖像快速亞像素邊緣檢測(cè)算法——基于正交多項(xiàng)式擬合的亞像素邊緣檢測(cè)算法。首先,利用傳統(tǒng)的Sobel算子完成邊緣點(diǎn)整像素級(jí)別的檢測(cè),確定邊緣的主體區(qū)域;然后,過(guò)邊緣點(diǎn)沿邊緣法線方向拓展像素,取一系列像素點(diǎn)并計(jì)算其灰度值;最后根據(jù)像素點(diǎn)灰度分布的數(shù)學(xué)特征,利用正交多項(xiàng)式和最小二乘法求擬合函數(shù),通過(guò)擬合曲線確定圖像邊緣點(diǎn)的精確位置,實(shí)現(xiàn)圖像亞像素邊緣檢測(cè)。實(shí)驗(yàn)證明,該算法運(yùn)行時(shí)間短,約為0.63 s;檢測(cè)精度高,可達(dá)0.1 pixels。
關(guān)鍵詞: 邊緣檢測(cè); 亞像素; Sobel;正交多項(xiàng)式; 曲線擬合
0 引言
在機(jī)械加工時(shí),刀具的幾何參數(shù)對(duì)數(shù)控機(jī)床的生產(chǎn)效率和加工質(zhì)量有著重大影響,因此,刀具必須在使用前明確其精確參數(shù)。目前,國(guó)內(nèi)常用的刀具測(cè)量方法,如機(jī)械式測(cè)量法、光學(xué)投影法等已無(wú)法滿足現(xiàn)代工業(yè)生產(chǎn)的要求,以圖像處理為核心的圖像測(cè)量技術(shù)具有高精度、高效率、非接觸和自動(dòng)化程度高等優(yōu)點(diǎn),能實(shí)現(xiàn)對(duì)刀具參數(shù)的精確檢測(cè)。圖像測(cè)量技術(shù)的實(shí)質(zhì)是提取刀具精確的輪廓邊緣,邊緣檢測(cè)是圖像處理的基礎(chǔ)和關(guān)鍵。傳統(tǒng)的邊緣檢測(cè)算法,如Sobel算子、Canny算子、LOG算子等雖然其形式簡(jiǎn)單,易實(shí)現(xiàn),速度快,但檢測(cè)精度不理想,僅能達(dá)到整像素級(jí)別,且對(duì)噪聲特別敏感,常產(chǎn)生偽邊緣。欲提高檢測(cè)系統(tǒng)的精度,通過(guò)優(yōu)化算法的軟處理比提高系統(tǒng)硬件分辨率的硬處理更加實(shí)用、有效[1]。
提出一種改進(jìn)的圖像亞像素邊緣檢測(cè)算法,利用傳統(tǒng)的Sobel算子和五次正交多項(xiàng)式最小二乘擬合原理實(shí)現(xiàn)邊緣精定位。
1亞像素邊緣檢測(cè)算法理論
1.1邊緣主體區(qū)域粗定位
Sobel算子既能確定邊緣點(diǎn)的位置和方向,還能根據(jù)像素點(diǎn)上下、左右鄰點(diǎn)的灰度加權(quán)差,對(duì)噪聲具有平滑作用,能提供較好的圖像邊緣信息,所以在邊緣主體區(qū)域粗定位時(shí)選用Sobel算子。Sobel算子是一種梯度幅值,其表現(xiàn)形式為:

其中,M(x,y)是像素點(diǎn)灰度值,Sx、Sy分別是邊緣點(diǎn)橫向、縱向的檢測(cè)灰度值。當(dāng)M(x,y)大于給定的閾值時(shí),可確定點(diǎn)(x,y)為邊緣點(diǎn),并根據(jù)Sx、Sy判斷梯度方向,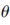 =arctan(Sy/Sx)。從圖1可以看出,Sobel算子對(duì)邊緣主體區(qū)域粗定位有很好的效果[2]。
=arctan(Sy/Sx)。從圖1可以看出,Sobel算子對(duì)邊緣主體區(qū)域粗定位有很好的效果[2]。

1.2 邊緣亞像素精定位
CCD是光強(qiáng)積分器件,在CCD采樣過(guò)程中,物空間突變的灰度在光學(xué)成像后會(huì)成為漸變的形式。如圖2(a)所示,圖像兩側(cè)分別表示背景和物體各自內(nèi)部的灰度變化情況,兩者之間表示圖像邊緣附近的灰度變化情況;如圖2(b)所示,沿邊緣法線方向,物體與背景內(nèi)部區(qū)域的灰度差分值微小,而邊緣附近的灰度差分最大,這就是經(jīng)典邊緣提取的理論。
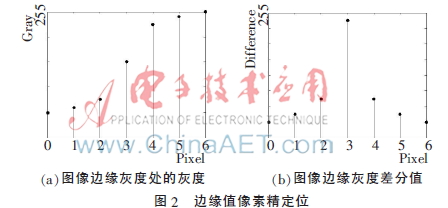
以上述理論為基礎(chǔ),對(duì)過(guò)粗定位所得邊緣點(diǎn),沿邊緣法線方向拓展像素,得到一系列過(guò)邊緣線的像素點(diǎn),求得這些點(diǎn)對(duì)應(yīng)的灰度值,然后根據(jù)這些點(diǎn)灰度分布的數(shù)學(xué)特征,利用五次正交多項(xiàng)式最小二乘法擬合原理求得擬合函數(shù)與曲線,再根據(jù)擬合曲線確定圖像邊緣亞像素點(diǎn)的位置,從而實(shí)現(xiàn)邊緣點(diǎn)的亞像素精確定位,這就是本文改進(jìn)的亞像素邊緣檢測(cè)算法的原理。
1.2.1 正交多項(xiàng)式擬合函數(shù)
在實(shí)際應(yīng)用中,要在保證檢測(cè)精度的前提下盡可能地縮短運(yùn)算時(shí)間,從而提高運(yùn)算效率,因此選擇適當(dāng)數(shù)量的邊緣點(diǎn)是十分重要的。選點(diǎn)過(guò)多會(huì)增加運(yùn)算時(shí)間,降低效率;選點(diǎn)過(guò)少會(huì)降低檢測(cè)精度,定位不準(zhǔn)。綜合以上因素,本課題選取5個(gè)像素點(diǎn),橫坐標(biāo)x代表像素值,其取值分別設(shè)為-2、-1、0、1、2,其縱坐標(biāo)y代表各點(diǎn)對(duì)應(yīng)的灰度值。根據(jù)施密特正交化公式[3]可得正交基函數(shù),如式1所示。
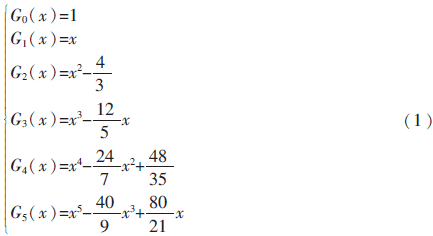
為了能取得較理想的擬合效果,選取[G0(x),G1(x),G2(x),G3(x),G4(x),G5(x)]為基底進(jìn)行擬合,擬合函數(shù)方程為:
F5(x)=a0·G0(x)+a1·G1(x)+a2·G2(x)+a3·G3(x)+a4·G4(x)+a5·G5(x)(2)
其中,a0、a1、a2、a3、a4、a5是五次正交多項(xiàng)式函數(shù)的未知系數(shù)[4]。
假設(shè)任一坐標(biāo)點(diǎn)(xi,yi)的橫、縱坐標(biāo)隨機(jī)誤差分別為pi、qi,則實(shí)測(cè)點(diǎn)坐標(biāo)到擬合曲線的距離殘差為:

全部點(diǎn)到曲線的距離殘差平方和為:
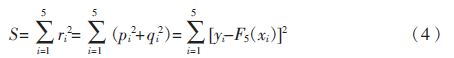
求取式(4)最小值min(S)時(shí),根據(jù)正交多項(xiàng)式最小二乘法擬合原理推導(dǎo)得系數(shù)為:
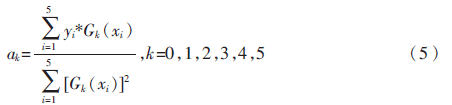
直接使用式(5)求多項(xiàng)式系數(shù)計(jì)算量大,較困難,且不能直觀體現(xiàn)各變量之間的內(nèi)在規(guī)律與聯(lián)系,因此對(duì)公式進(jìn)行變換轉(zhuǎn)化為如下更直觀的矩陣表達(dá)式:
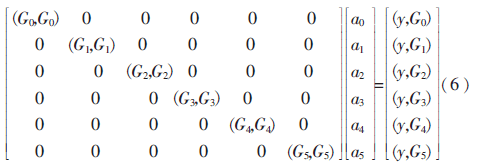
由式(6)可求得多項(xiàng)式系數(shù)值:
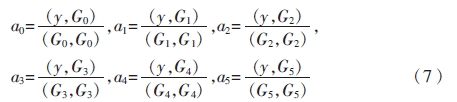
將式(7)代入式(2)得擬合函數(shù)F5(x):

1.2.2 計(jì)算圖像邊緣位置
根據(jù)亞像素邊緣檢測(cè)原理可知,擬合函數(shù)表達(dá)式F5(x)是以點(diǎn)的灰度值為基本元素求得的。從數(shù)學(xué)意義上來(lái)講,F(xiàn)5(x)描述了圖像邊緣線的情況,而函數(shù)一階微分

則描述了邊緣線變化程度的情況,即點(diǎn)的灰度值變化率的情況。那么,函數(shù)二階微分

則描述了點(diǎn)的灰度值變化率的變化情況。
由以上分析可知,亞像素點(diǎn)的位置就是點(diǎn)的灰度值變化率變化最大的位置,依據(jù)極值求解條件,將函數(shù)F5(x)對(duì)x求二階微分并令其等于零,即

求得x的數(shù)值即是亞像素點(diǎn)的位置。
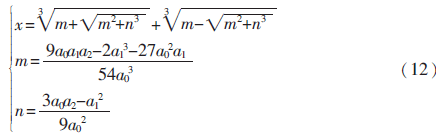
2 亞像素邊緣檢測(cè)算法的實(shí)驗(yàn)
利用Visual C++6.0語(yǔ)言在MATLAB V201b2軟件平臺(tái)編寫(xiě)Sobel算子和本文改進(jìn)的算法程序?qū)崿F(xiàn)對(duì)圖像的數(shù)字處理。
實(shí)驗(yàn)1 算法抗噪性能研究
圖像信噪比等于信號(hào)與噪聲的功率譜之比。由此可知,邊緣點(diǎn)的檢測(cè)精度與噪聲成負(fù)相關(guān)關(guān)系。分別用兩種算法處理圖像,效果如圖3所示。可以看出,本文算法與Sobel算子相比同樣具有完整且較細(xì)的邊緣,但前者生成的噪點(diǎn)明顯更少,因而具有更好的抗噪聲性能。

實(shí)驗(yàn)2 算法檢測(cè)精度研究[5]

制作了尺寸為100×100的二值化圖像,如圖4所示。白色矩形所在區(qū)域的灰度值為0,其余背景灰度值為255,底邊在圖像第20行、第20~80列位置上。首先提取了部分邊緣點(diǎn)理論坐標(biāo)值,再使用改進(jìn)的算法處理圖像并提取了相應(yīng)邊緣點(diǎn)的亞像素坐標(biāo)檢測(cè)值,如表1所示。通過(guò)分析與計(jì)算可知改進(jìn)算法的檢測(cè)精度。
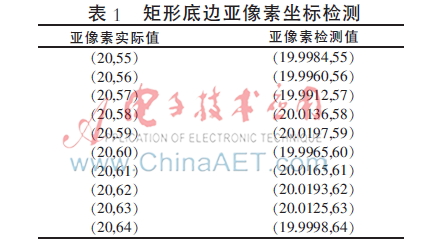
以單個(gè)像素點(diǎn)坐標(biāo)理論值與檢測(cè)值的坐標(biāo)差值作為算法偏差,經(jīng)計(jì)算可得其標(biāo)準(zhǔn)偏差約為0.1 pixels。
實(shí)驗(yàn)3 算法時(shí)間研究
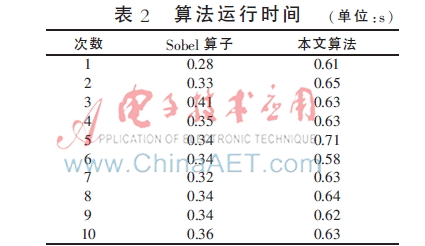
取尺寸為1 600×1 455的同一圖像在同一實(shí)驗(yàn)平臺(tái)進(jìn)行多次測(cè)試,得到多組運(yùn)行時(shí)間,如表2所示。為了提高數(shù)據(jù)的可靠性,首先從數(shù)據(jù)中去掉一個(gè)最小值和一個(gè)最大值,再求取其他組的平均值作為運(yùn)行時(shí)間。經(jīng)計(jì)算,Sobel處理時(shí)間約為0.34 s,本文算法的處理時(shí)間約為0.63 s。
3 結(jié)束語(yǔ)
從理論分析與仿真實(shí)驗(yàn)可以看出,本文改進(jìn)的亞像素邊緣檢測(cè)算法具有抗噪性能強(qiáng)、檢測(cè)精度高、運(yùn)行速度快的優(yōu)點(diǎn),主要適用于對(duì)處理速度和檢測(cè)精度要求較高的機(jī)器視覺(jué)檢測(cè)系統(tǒng),而且已試用于數(shù)控機(jī)床刀具預(yù)調(diào)測(cè)量?jī)x,極大地提高了數(shù)控機(jī)床的效能,運(yùn)行穩(wěn)定、可靠。
參考文獻(xiàn)
[1] 李東光,景芳盛,張國(guó)雄.計(jì)算機(jī)視覺(jué)二維刀具預(yù)調(diào)測(cè)量?jī)x的研究[J].制造技術(shù)與機(jī)床,2001(5):20-22.
[2] 劉力雙,張銚,盧慧卿,等.圖像的快速亞像素邊緣檢測(cè)算法[J].光電子·激光,2005,16(8):993-996.
[3] 王新民,術(shù)洪亮.工程數(shù)學(xué)計(jì)算方法[M].北京:高等教育出版社,2005.
[4] 徐中宇,寧闖,周亞洲.一種快速亞像素邊緣檢測(cè)算法[J].吉林大學(xué)學(xué)報(bào)(理學(xué)版),2014,52(2):308-313.
[5] PERKINS W A. INSPECTOR: a computer vision system which Learn to inspect parts[C]. IEEE Trans. on Pattern Analysis and Machine Intelligence,PAMI-5,1983:584-592.

