摘 要: 為解決現(xiàn)有船舶交通流量預(yù)測(cè)算法中存在的預(yù)測(cè)精度不高、算法穩(wěn)定性差等不足,,將一種數(shù)據(jù)融合BP神經(jīng)網(wǎng)絡(luò)的算法用于船舶流量的預(yù)測(cè),,不僅能較好地實(shí)現(xiàn)船舶流量的高精度預(yù)測(cè),而且還增強(qiáng)了算法的穩(wěn)定性,。以寧波港口2012年船舶流量觀察數(shù)據(jù)為實(shí)例進(jìn)行分析,,用MATLAB軟件編程進(jìn)行系統(tǒng)仿真,實(shí)驗(yàn)結(jié)果表明,,經(jīng)過(guò)數(shù)據(jù)融合的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)精度高,,系統(tǒng)魯棒性強(qiáng),預(yù)測(cè)效果明顯優(yōu)于傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)算法,。
關(guān)鍵詞: 數(shù)據(jù)融合,;神經(jīng)網(wǎng)絡(luò);船舶流量,;預(yù)測(cè)
近年來(lái),,水運(yùn)總量突飛猛進(jìn),造就了我國(guó)沿海及長(zhǎng)江流域等地的各條“黃金水道”,,為我國(guó)的經(jīng)濟(jì),、社會(huì)發(fā)展做出了重要貢獻(xiàn),。但同時(shí),水運(yùn)量的增加使水上交通事故頻發(fā),,造成了巨大的損失,,這對(duì)水道的設(shè)計(jì)、規(guī)劃和船舶通航資源管理的優(yōu)化配置提出了更高的要求,。船舶流量預(yù)測(cè)的研究為水道的設(shè)計(jì),、規(guī)劃和船舶通航管理提供了基礎(chǔ)性依據(jù)。
參考文獻(xiàn)[1]提出差分序列特性進(jìn)行模型的篩選和基于模糊變權(quán)重的船舶交通流量組合預(yù)測(cè)方法實(shí)現(xiàn)了船舶流量的預(yù)測(cè),。參考文獻(xiàn)[2]根據(jù)組合預(yù)測(cè)的思想,,將三種算法進(jìn)行智能融合構(gòu)建一種新的智能預(yù)測(cè)系統(tǒng)。參考文獻(xiàn)[3]利用系統(tǒng)工程的相關(guān)原理,,提出了基于BP神經(jīng)網(wǎng)絡(luò)的數(shù)學(xué)模型,。以上方法各有優(yōu)缺點(diǎn),預(yù)測(cè)精度往往不高,,算法穩(wěn)定性較差,。為此,本文提出一種數(shù)據(jù)融合的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法,,進(jìn)一步提高船舶流量的預(yù)測(cè)精度及算法的穩(wěn)定性,。
1 船舶交通流量預(yù)測(cè)原理
船舶流量預(yù)測(cè)指定性預(yù)測(cè)和定量預(yù)測(cè)[4]。船舶流量的預(yù)測(cè)主要受客觀環(huán)境和算法模型影響,,拋開客觀因素,,算法將是解決預(yù)測(cè)精度不高的主要因素。船舶流量的預(yù)測(cè)具有時(shí)變,、不確定,、非線性特征,神經(jīng)網(wǎng)絡(luò)模型[5]具有很強(qiáng)的非線性預(yù)測(cè)能力和泛化能力,。本文在選取BP神經(jīng)網(wǎng)絡(luò)模型時(shí),,引入數(shù)據(jù)融合機(jī)制,其預(yù)測(cè)原理結(jié)構(gòu)如圖1所示,。

2 數(shù)據(jù)融合BP算法模型
2.1 BP神經(jīng)網(wǎng)絡(luò)算法原理
BP神經(jīng)網(wǎng)絡(luò)算法[6]的原理是:輸入量Xi通過(guò)隱含層作用于輸出節(jié)點(diǎn),,經(jīng)非線性變換,產(chǎn)生輸出量Yk,,網(wǎng)絡(luò)訓(xùn)練的每個(gè)樣本包括輸入向量和期望輸出量,,通過(guò)調(diào)整輸入節(jié)點(diǎn)與隱層節(jié)點(diǎn)的權(quán)值Wij和隱層節(jié)點(diǎn)與輸出節(jié)點(diǎn)之間的權(quán)值Tjk以及閾值,使網(wǎng)絡(luò)輸出值與期望輸出值之間的偏差沿梯度方向下降,,經(jīng)過(guò)網(wǎng)絡(luò)訓(xùn)練,,確定最小誤差對(duì)應(yīng)的網(wǎng)絡(luò)參數(shù),訓(xùn)練停止,。網(wǎng)絡(luò)結(jié)構(gòu)如圖2所示,。
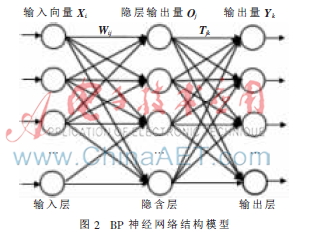
2.2 BP算法描述
采集船舶流量VTS數(shù)據(jù),,預(yù)處理成BP神經(jīng)網(wǎng)絡(luò)模型訓(xùn)練的樣本,然后根據(jù)BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)建立最佳模型,。Xi為輸入向量,,Oj為隱層輸出向量,Yk為輸出向量,,Wij為第i個(gè)輸入層到第j個(gè)隱含層之間的權(quán)值,,Tjk為第j個(gè)隱含層到第k個(gè)輸出層之間的權(quán)值。
f為非線性神經(jīng)元函數(shù),,為神經(jīng)單元閾值,,則:

激勵(lì)函數(shù)是反映下層輸入對(duì)上層節(jié)點(diǎn)刺激脈沖強(qiáng)度的函數(shù),又稱刺激函數(shù),,一般取(0,1)內(nèi)連續(xù)取值的Sigmoid函數(shù):
f(x)=1/(1+e-x)(3)
誤差計(jì)算模型是反映神經(jīng)網(wǎng)絡(luò)期望輸出與計(jì)算輸出之間誤差大小的函數(shù),Tpi為節(jié)點(diǎn)的期望輸出值,;Opi為節(jié)點(diǎn)計(jì)算輸出值,。

神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)過(guò)程,即連接下層節(jié)點(diǎn)和上層節(jié)點(diǎn)之間的權(quán)重矩陣Wij的設(shè)定和誤差修正過(guò)程,。自學(xué)習(xí)模型中?濁為學(xué)習(xí)因子,,Фi為輸出節(jié)點(diǎn)i的計(jì)算誤差,Oj為輸出節(jié)點(diǎn)j的計(jì)算輸出,,a為動(dòng)量因子,,則:

在運(yùn)用BP神經(jīng)網(wǎng)絡(luò)算法時(shí)通常方法為歸一化處理[7],將其轉(zhuǎn)換成適合激勵(lì)函數(shù)Sigmoid區(qū)間的數(shù)據(jù)變量,,作為神經(jīng)網(wǎng)絡(luò)訓(xùn)練的樣本,。
2.3 數(shù)據(jù)融合算法
單純用BP神經(jīng)網(wǎng)絡(luò)算法獲取的預(yù)測(cè)值必定存在較大的誤差,降低甚至消除這些誤差對(duì)提高預(yù)測(cè)精度具有十分重要的意義,。通過(guò)一種數(shù)據(jù)融合優(yōu)化手段,,將BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)獲取的初步預(yù)測(cè)結(jié)果進(jìn)一步優(yōu)化,步驟如下:
(1)搭建BP神經(jīng)網(wǎng)絡(luò)算法模型,,進(jìn)行多次訓(xùn)練獲得船舶流量的多條預(yù)測(cè)曲線L(1),,L(2),L(3),,…,,L(n)。
(2)將這些曲線進(jìn)行加權(quán)平均得到一條平均曲線L(a):

(3)構(gòu)造新的曲線空間,。L(1),,L(2),L(3),,…,,L(n)與平均曲線L(a)作差,,記錄偏差最大的曲線為L(zhǎng)(j1),L(j2),,…,,L(jj),將其剔除,,保留剩下的曲線并重新編號(hào)為L(zhǎng)(1),,L(2),…,,L(n-j)構(gòu)成新曲線空間,。
(4)新的曲線空間中再次作數(shù)據(jù)融合加權(quán)平均,得到一條較優(yōu)的預(yù)測(cè)曲線L:

經(jīng)過(guò)這種多次預(yù)測(cè)剔除偏差較大曲線的數(shù)據(jù)融合加權(quán)平均處理可以有效地提高預(yù)測(cè)精度,。
(5)獲取較優(yōu)預(yù)測(cè)曲線L中的k個(gè)值L1,,L2,L3,,…,,Lk,與期望預(yù)測(cè)值T的k個(gè)分量T1,,T2,,…,Tk作差,,取絕對(duì)平均值M,,如式(8)所示:
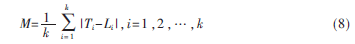
(6)對(duì)較優(yōu)預(yù)測(cè)曲線L中的k個(gè)值依次進(jìn)行判斷,并且剔除偏離門限的點(diǎn)值,,利用線性插補(bǔ)法填充剔除的點(diǎn),。
(7)獲取平滑系數(shù):
Ri=1+Bi(9)
其中,Ri表示第i個(gè)值的平滑系數(shù),,即為平滑的權(quán)重,;Bi表示Ti與Li的殘差Ei所占毛誤差E的比例程度:

其中,h為比例程度系數(shù),,取10-n,,n為正整數(shù),此處n取1,。
(8)進(jìn)行數(shù)據(jù)的平滑,。假設(shè)有k個(gè)預(yù)測(cè)值,Li表示第i個(gè)預(yù)測(cè)值,,其中,,i=1,2,3,,…,,k。Hi表示平滑后的最終預(yù)測(cè)值,。
Hi=Ri×Li(13)
數(shù)據(jù)融合BP技術(shù)[8]預(yù)測(cè)曲線平滑的過(guò)程引入了多次預(yù)測(cè)并刪除誤差較大預(yù)測(cè)曲線及曲線點(diǎn)的數(shù)據(jù)處理機(jī)制,,使得算法在預(yù)測(cè)精度不斷提高的同時(shí),有效地提高了系統(tǒng)的容錯(cuò)能力,,即使在預(yù)測(cè)過(guò)程中產(chǎn)生了一些誤差較大甚至嚴(yán)重偏離船舶交通流量真實(shí)曲線的預(yù)測(cè)值,,這些預(yù)測(cè)值也會(huì)在多次預(yù)測(cè)中剔除異常數(shù)據(jù)的處理下被刪除,較好地降低預(yù)測(cè)誤差的同時(shí)提高了船舶交通流量的預(yù)測(cè)精度,,使預(yù)測(cè)算法具有較好的穩(wěn)定性,。
3 實(shí)驗(yàn)結(jié)果分析
3.1 預(yù)測(cè)仿真結(jié)果
結(jié)合上述算法分析流程,采集寧波港口2012年7月5日~8月9日船舶流量VTS數(shù)據(jù)作為原始數(shù)據(jù),,預(yù)測(cè)仿真結(jié)果分析如下:
先根據(jù)訓(xùn)練好的BP神經(jīng)網(wǎng)絡(luò)算法對(duì)船舶流量進(jìn)行預(yù)測(cè),,預(yù)測(cè)結(jié)果與實(shí)際船舶交通流量VTS觀測(cè)數(shù)據(jù)對(duì)比,如圖3所示,。
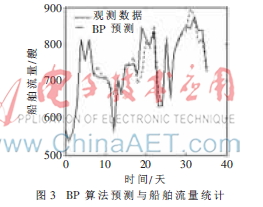
由圖3可知,,BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法在整體上雖有一定的預(yù)測(cè)精度,但部分預(yù)測(cè)結(jié)果偏差較大,,預(yù)測(cè)精度還有待提高,需進(jìn)一步研究,。
數(shù)據(jù)融合BP神經(jīng)網(wǎng)絡(luò)算法在傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)算法的基礎(chǔ)上引入數(shù)據(jù)融合思想,,用BP神經(jīng)網(wǎng)絡(luò)進(jìn)行100次仿真,將每次預(yù)測(cè)結(jié)果與平均預(yù)測(cè)結(jié)果作差比較,,刪除一些誤差較大的預(yù)測(cè)結(jié)果,;然后將剩余的預(yù)測(cè)結(jié)果經(jīng)過(guò)數(shù)據(jù)加權(quán)平均融合獲取一條較優(yōu)的曲線;接著對(duì)較優(yōu)曲線進(jìn)一步優(yōu)化,,采用數(shù)據(jù)融合管理機(jī)制,,以預(yù)測(cè)結(jié)果的殘差所占總體誤差的大小來(lái)設(shè)定門限,剔除門限之外的點(diǎn)值,,并以線性插補(bǔ)的方法填充剔除點(diǎn),;最后對(duì)較優(yōu)點(diǎn)值進(jìn)行平滑優(yōu)化,獲得一條高精度的預(yù)測(cè)曲線,。其仿真結(jié)果與原始觀測(cè)數(shù)據(jù)比較結(jié)果如圖4所示,。

從圖3和圖4可以看出,經(jīng)過(guò)數(shù)據(jù)融合BP神經(jīng)網(wǎng)絡(luò)算法的預(yù)測(cè)結(jié)果偏離實(shí)際值較小,,更接近于船舶交通流量的實(shí)際值,,預(yù)測(cè)精度更高,預(yù)測(cè)效果明顯優(yōu)于傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法,,而且算法穩(wěn)定性更強(qiáng),。
3.2 算法穩(wěn)定性及有效性分析
本文在理論分析及實(shí)驗(yàn)結(jié)果的基礎(chǔ)上以算法的方差大小來(lái)判斷算法的穩(wěn)定性,,以平均絕對(duì)誤差(MAE)、平均絕對(duì)百分誤差(MAPE),、均方根誤差(RMSE),、均方根誤差比(RMSEP)來(lái)衡量?jī)煞N算法的預(yù)測(cè)精度的有效性。圖5為兩種算法方差/10的對(duì)比圖,。

由圖5可知,,數(shù)據(jù)融合BP神經(jīng)網(wǎng)絡(luò)算法預(yù)測(cè)結(jié)果的方差明顯小于傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法預(yù)測(cè)結(jié)果的方差,從而說(shuō)明數(shù)據(jù)融合BP算法的穩(wěn)定性更優(yōu)越,。上述數(shù)據(jù)融合BP預(yù)測(cè)算法引入了數(shù)據(jù)融合處理機(jī)制,,使得算法在預(yù)測(cè)精度不斷提高的同時(shí),有效地提高了算法的抗干擾能力,,即使在預(yù)測(cè)過(guò)程中有較大預(yù)測(cè)誤差與測(cè)量誤差的影響,,這些預(yù)測(cè)值也會(huì)在多次估計(jì)剔除異常數(shù)據(jù)的處理下被刪除,較好地降低了預(yù)測(cè)誤差對(duì)預(yù)測(cè)精度的影響,,使數(shù)據(jù)融合BP預(yù)測(cè)算法具有較好的穩(wěn)定性,,從而增強(qiáng)了系統(tǒng)的魯棒性。
令實(shí)際測(cè)量值為Ti,,預(yù)測(cè)值為Hi,,n為觀察數(shù)據(jù)的總數(shù)量,預(yù)測(cè)準(zhǔn)確度的指標(biāo)如下:
平均絕對(duì)誤差MAE和平均絕對(duì)百分誤差MAPE分別為:

統(tǒng)計(jì)得到寧波港口2012年7月5日~8月9日船舶交通流量VTS總量為26 510艘,。傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法預(yù)測(cè)的結(jié)果為26 415艘,,數(shù)據(jù)融合BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法預(yù)測(cè)的結(jié)果為26 492艘,兩種算法預(yù)測(cè)精度性能指標(biāo)比較如表1所示,。

從表1可以明顯看出,,數(shù)據(jù)融合BP預(yù)測(cè)算法的預(yù)測(cè)精度各項(xiàng)指標(biāo)均明顯優(yōu)于傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法,其預(yù)測(cè)精度更高,,算法穩(wěn)定性能更強(qiáng),。
經(jīng)過(guò)數(shù)據(jù)融合的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法,在傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法的基礎(chǔ)上引入數(shù)據(jù)融合優(yōu)化處理機(jī)制,,有效提高了船舶交通流量的預(yù)測(cè)精度,,合理改善了算法的穩(wěn)定性,而且智能地調(diào)整了數(shù)據(jù)融合預(yù)測(cè)權(quán)值系數(shù)的比例關(guān)系,。此外,,結(jié)合門限偏差值的設(shè)定剔除偏差較大軌跡點(diǎn),并進(jìn)行線性插補(bǔ)剔除的點(diǎn),,最后將曲線值進(jìn)行平滑處理,,獲取最優(yōu)的預(yù)測(cè)結(jié)果。該算法能夠較好地實(shí)現(xiàn)船舶交通流量的高精度預(yù)測(cè),同時(shí)有效提高了算法的穩(wěn)定性,,與傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)算法相比,,其獨(dú)特的數(shù)據(jù)融合算法較好地實(shí)現(xiàn)了曲線點(diǎn)值偏移量的數(shù)據(jù)融合優(yōu)化匹配管理,有效地提高了預(yù)測(cè)精度,,并具有計(jì)算復(fù)雜度低,、穩(wěn)定性強(qiáng)、適用范圍廣等優(yōu)點(diǎn),。
參考文獻(xiàn)
[1] 楊翔.船舶交通流量預(yù)測(cè)方法研究[D].大連:大連海事大學(xué),,2006.
[2] 黃洪瓊,湯天浩,,金永興,,等.基于智能融合的船舶交通流預(yù)測(cè)系統(tǒng)[J].中國(guó)航海,2008,,31(4):364-367.
[3] 王東.基于BP人工神經(jīng)網(wǎng)絡(luò)的船舶交通流量預(yù)測(cè)研究[D].武漢:武漢理工大學(xué),,2009.
[4] 郎茂祥,傅選義,,朱廣宇.預(yù)測(cè)理論與方法[M].北京:北京交通大學(xué)出版社,,2011.
[5] 周開利,康耀紅.神經(jīng)網(wǎng)絡(luò)模型及其MATLAB仿真程序設(shè)計(jì)[M].北京:清華大學(xué)出版社,,2005.
[6] 蔣良孝,,李超群.基于BP神經(jīng)網(wǎng)絡(luò)的函數(shù)逼近方法及MATLAB實(shí)現(xiàn)[J].微型機(jī)與應(yīng)用,2004,,23(1):52-53.
[7] 李曉峰,,徐玖平,王蔭清,,等.BP人工神經(jīng)網(wǎng)絡(luò)自適應(yīng)學(xué)習(xí)算法的建立及其應(yīng)用[J].系統(tǒng)工程理論與實(shí)踐,2004,,24(5):1-8.
[8] 吳祖堂.基于神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)器的傳感器數(shù)據(jù)證實(shí)技術(shù)研究[J].電子技術(shù)應(yīng)用,,2001,27(1):22-25.

