0 引言

    隨著電子產品向輕、薄,、短,、小的趨勢發(fā)展，在互連基板內層制造或埋入無源器件以實現(xiàn)元件高密度集成的埋入式無源器件技術受到廣泛關注,。該技術可有效減小基板面積,，提高布線密度,，降低生產成本。然而元件集成度提高的同時基板內單位體積的功耗增大,、發(fā)熱量增加,，高溫環(huán)境影響埋入式器件的工作壽命并導致相關參數值改變，當溫度升高到一定程度,，埋入式器件可能因失效而停止工作,。因此有必要對埋入式基板的散熱問題進行研究，分析參數不同的元器件相互間的位置關系對溫度場分布的影響,，尋求散熱效果最佳的布局方案,，保證基板正常工作。

    電子元件布局屬于組合優(yōu)化問題,，遺傳算法是計算數學中的一種全局優(yōu)化算法,，非常適合解決大規(guī)模的組合優(yōu)化問題。近年來已有學者將遺傳算法應用到該領域研究中,，如文獻[1]利用遺傳算法解決單層SMT電子元件的熱布局優(yōu)化,，文獻[2，3]利用遺傳算法進行兩層3D-MCM芯片的熱布局設計等,。但由于遺傳算法存在特有的早熟收斂現(xiàn)象, 在進化早期種群多樣性急劇減少,，群體缺乏有效的等位基因，在遺傳算子作用下不再生成高階競爭模式,。因此,，采用標準遺傳算法進行熱布局優(yōu)化得到的優(yōu)化結果有可能并非全局最優(yōu)解，而是某個隨機的非優(yōu)個體,。

    本文以埋入式無源器件為研究對象,，針對標準遺傳算法在電子元件熱布局優(yōu)化中存在的問題，通過改進以熱疊加模型為基礎的適應度函數,，采用模糊邏輯控制器自適應調整遺傳算法的交叉概率和變異概率,，提高搜索全局最優(yōu)解的精確度，以及對長時間未進化的種群執(zhí)行局部災變等措施維持種群多樣性并抑制早熟收斂,，以獲得更好的布局排列,。

1 埋入式電阻布局描述

    埋入式無源器件的主要發(fā)熱源是電阻元件，電阻的功率對PCB板的溫升具有顯著影響,，且電阻在基板中的位置不同,，其溫升不同，對鄰近器件的溫度影響也不同^[4],。不合理的布局將導致基板局部溫度過高或溫度梯度過大,，從而降低電路板的整體性能及可靠性。本文采用模糊遺傳算法對埋入式電阻的位置布局進行優(yōu)化,得到電阻在某種散熱條件下的最優(yōu)布局,使埋入式基板內部各處溫度趨于平均和最高溫度降低。為簡化計算,本文將功耗不同,、材料和尺寸相同的電阻在基板內部建立一個兩層布局排列,，如圖1所示，底層和上層各有9個電阻,底層電阻和頂層電阻每兩個重疊在一起,。在采用遺傳算法進行布局優(yōu)化的過程中需要對電阻的位置進行編碼,則先對各電阻進行編號(從1～18),，數字編號對應其相應功率,也表示電阻的位置,電阻1的功率最小,電阻18的功率最大。

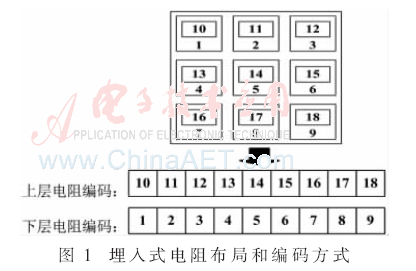
2 模糊遺傳算法優(yōu)化埋入式電阻布局

2.1 適應度函數設計

    在利用遺傳算法進行電子元件優(yōu)化布局設計時,，通常以電子元件的溫度為優(yōu)化目標,，當溫度達到最小時為最優(yōu)解。文獻[1-3]采用Balwant Singh Lall等人提出的熱疊加模型中的溫度計算公式^[5]作為遺傳算法的適應度函數,，其基本原理是：在計算任一處電子元件的溫度時,，除考慮相鄰電子元件發(fā)熱產生的影響外，還需考慮其他電子元件對此處的熱量貢獻,。在電子元件上的熱分布是：元件中心最熱,，隨著與中心距離的增加，熱分布單調降低,。由此得到電子元件內,、外熱分布方程分別為：

其中B_i為畢奧數，I₀和I₁為變形的第一類0階和1階貝塞爾函數,，K₀和K₁為變形的第二類0階和1階貝塞爾函數,。

    利用疊加原理，由式(1)得到電子元件上任一點溫度,；為簡化計算,，以電子元件中心處的溫度表示該元件溫度，因此D⁺=0,，I₀=1,，式(1)簡化為：

    由式(3)可以求出各電子元件的自身溫度T_io，由式(2)求出某一元件j對元件i的貢獻溫度T_ji,，因此,，可得每一個元件在基板上的溫度：

式中M為基板中電子元件的總數。則遺傳算法的適應度函數定義為所有電子元件溫度的平均值：

    由于計算式(2)和式(3)需貝塞爾函數,，為降低計算復雜度,，采用多項式方程簡化后^[6]，得到某一元件i的自身溫度為：

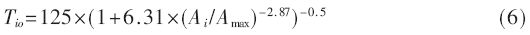
式中A_i為某一元件i的功率,，A_max為所有元件中的最大功率,；某一元件j對元件i的貢獻溫度為：

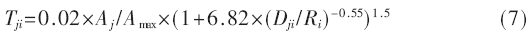
D_ji表示元件j和元件i的距離，R_i為元件i半徑,。

    然而,，通過大量仿真實驗發(fā)現(xiàn)，以式(5)所示的適應度函數作為遺傳進化目標的缺點是搜索到的最優(yōu)布局不具有唯一性,。

    針對上述問題,，算法在原適應度函數式(5)的基礎上增加了兩個修正項，如式(8)所示,，Ave為原適應度函數值,，修正項Max代表所有元件的最高溫度，修正項Diff代表元件最高溫度與最低溫度的差值,。公式中各項參數權重的最優(yōu)取值由實驗驗證得到,。以0.1為步長，Ave項的權重從0～1遍歷取值,，修正項Max和Diff的權重在此基礎上取遍所有可能的組合,，經仿真實驗反復驗證，當Ave項權重為0.8,、兩個修正項的權重均為0.1時,，搜索效果最佳。修正后的適應度函數與式(5)相比評價標準更全面,，可有效防止遺傳進化過程中因單一進化目標而陷入局部最優(yōu)解,。   

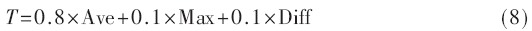
2.2 模糊邏輯控制器設計

    本文采用模糊邏輯控制器自適應調整遺傳算法參數的思路，如圖2所示,，模糊邏輯控制器有兩個輸入變量和兩個輸出變量,，輸入變量為遺傳算法的當前進化代數gen，以及進化過程中最優(yōu)適應度值未改變的次數num,，輸出變量為遺傳算法的交叉概率P_c和變異概率P_m,。各輸入變量的模糊論域都歸一化到[0,1]范圍，輸出變量P_c和P_m的論域分別為[0.7,1]和[0,，0.3],。

    模糊邏輯控制器的規(guī)則如表1所示，各輸入,、輸出變量的語言值都設為三個,，分別是S、M 和B,，對于輸入變量gen,，S代表進化早期，M 代表進化中期,，B代表進化后期,；對于其他變量，S代表小,，M 代表中,，B代表大,。共有9條規(guī)則。規(guī)則1～3表示進化早期,，種群多樣性較好,，P_c和P_m隨著num變化相應增大或減小,；規(guī)則4～6表示進化中期,，種群多樣性逐漸下降，對P_c和P_m賦值力度比早期偏大,；規(guī)則7～9表示進化后期,，種群趨于收斂，為避免破壞已找到的最優(yōu)解,，對P_c和P_m的賦值力度比早期偏小,。

    在某些極端情況下，當自適應調整交叉概率和變異概率也無法阻止種群多樣性在進化早期迅速衰減時,，需相應的人工干預以維持種群多樣性,，防止種群過早收斂。具體措施是在進化早期或中期,，對超過50代沒有尋找到更優(yōu)適應度值的種群執(zhí)行局部災變,，將種群中適應度值最差的10%個體更換為當前種群最優(yōu)個體不同變異體。

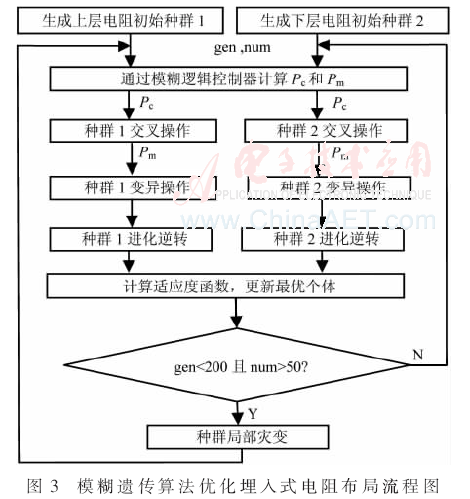
    圖3是模糊遺傳算法優(yōu)化埋入式電阻布局的主要流程,，算法分別對上下層電阻實施遺傳操作,，依次執(zhí)行初始種群生成、交叉,、變異和進化逆轉操作,，但共用模糊邏輯控制器輸出的交叉概率P_c和變異概率P_m，而在計算適應度函數和局部災變時,，將兩個種群作為整體進行評價及更新,。

2.3 熱布局優(yōu)化實現(xiàn)及結果

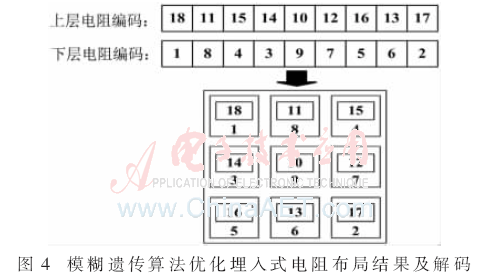
    表2為標準遺傳算法與模糊遺傳算法優(yōu)化兩層埋入式電阻布局的300次統(tǒng)計結果對比分析，標準遺傳算法在進化早期收斂的比率約占30%,，在進化中后期正常收斂的比例不足50%,，在進化末期遲滯收斂的比例也偏高，占22%,，且早熟收斂和遲滯收斂所得的平均最優(yōu)解都高于進化中后期正常收斂所得最優(yōu)解,。模糊遺傳算法在進化早期收斂比例下降到1.67%，而有81%的概率能夠在進化中后期正常收斂,，在進化末期遲滯收斂的比例也較標準遺傳算法下降了約5%,，且在進化中后期搜索到的平均最優(yōu)解比早熟收斂和遲滯收斂時得到的解更優(yōu)。圖4是模糊遺傳算法300次計算中搜索到的最優(yōu)布局結果,，由此得到的熱布局規(guī)則是：上層各大功率電阻分布于四角,，小功率電阻圍繞在大功率電阻周圍,；下層電阻的分布應盡量避免上下層大功率電阻疊在一起，造成局部溫度過高,。

3 優(yōu)化結果有限元仿真實驗驗證

    為驗證模糊遺傳算法的熱布局優(yōu)化效果,，將優(yōu)化前隨機布局、采用標準遺傳算法及模糊遺傳算法的優(yōu)化布局結果（見圖5）使用ANSYS有限元分析軟件建立熱分析模型,，對溫度場分布情況進行對比分析。

    有限元熱分析模型的參數設置如下：PCB板的材料是FR-4,，熱導率為1.7 W/(m·K),，環(huán)境溫度是22 ℃，表面對流冷卻系數是25 W/(m²·K),；埋入式電阻尺寸為2 mm×1.25 mm×0.5 mm,。

    圖6和表3是采用有限元熱分析得到的三種布局的溫度場分布及相關參數統(tǒng)計。從以上圖表可知,，與優(yōu)化前隨機布局及標準遺傳算法優(yōu)化布局結果相比,，模糊遺傳算法的優(yōu)化布局結果其溫度場分布更均勻，且在基板的最高溫度方面,，優(yōu)化前隨機布局為69.015 ℃,，標準遺傳算法的優(yōu)化布局結果為63.849 ℃，模糊遺傳算法的優(yōu)化布局結果為53.668 ℃,，與前兩種布局相比分別下降了15.347 ℃和10.181 ℃,；在最大溫差方面，優(yōu)化前隨機布局為13.396 ℃,，標準遺傳算法的優(yōu)化布局結果為12.073 ℃,，模糊遺傳算法的優(yōu)化布局結果為10.6 ℃，較前兩種布局分別下降了2.796 ℃和1.473 ℃,。

4 優(yōu)化結果實驗驗證

    為進一步驗證模糊遺傳算法的熱布局優(yōu)化結果的正確性,，本文還根據模糊遺傳算法的熱布局優(yōu)化結果制作相應的測試樣件，對測試樣件進行通電測試并測量樣件在通電后的溫度分布結果,，以此驗證熱布局優(yōu)化量樣件在通電后的溫度分布結果,，以此驗證熱布局優(yōu)化結果的正確性。

    實驗測試樣件制作時首先選取長度為15 cm,、寬度為10 cm,、厚度為2 mm的雙面覆銅PCB板，使用數控機床加工出凹槽,，在PCB板上,、下兩面形成雙面對稱、深度為0.6 mm的凹槽（單面三條,、雙面共六條凹槽）,。所有凹槽槽寬均為2 mm,，槽間距5 mm。再按照圖5的三種布局排列,，將相應阻值的電阻分別埋入所開的上,、下凹槽槽內，從而形成與圖7所示布局一致的上,、下兩層的埋入式電阻布局,。各埋入電阻之間采用串聯(lián)形式、利用銅線進行連接,。實驗選用的電阻為0805型貼片電阻,，幾何尺寸為2 mm×1.25 mm×0.5 mm。在完成電阻的電氣連接后,，再使用環(huán)氧樹脂將所有凹槽進行填充,，從而最終實現(xiàn)所需的埋入式電阻布局。圖7所示即為經過環(huán)氧樹脂填充后不同埋入式電阻布局的實驗樣件,。（圖中所示僅為上表面凹槽內埋入的9個電阻）,。

    制作完不同埋入式電阻布局的實驗測試樣件后，對各個實驗樣件通電,。為使電阻產生更多的熱量以利于溫度測量,，選擇加載220 V交流電。通電20 min后,，利用熱成像儀對各個實驗樣件溫度進行檢測,，得到如圖8所示三種布局的溫度分布圖，各種布局下的實測溫度參數如表4所示,。

    由圖8和表4所示數據可知,，實驗樣件的熱成像溫度分布測試結果與有限元熱分析的仿真結果基本一致，在電路板的最高溫度方面,，優(yōu)化前隨機布局為66 ℃,，標準遺傳算法的優(yōu)化布局結果為59 ℃，模糊遺傳算法的優(yōu)化布局結果為51 ℃,，與前兩種布局相比分別下降了15 ℃和8 ℃,；在最大溫差方面，優(yōu)化前隨機布局為8 ℃,，標準遺傳算法的優(yōu)化布局結果為7 ℃,，模糊遺傳算法的優(yōu)化布局結果為5 ℃，較前兩種布局分別下降了3 ℃和2 ℃,，從而驗證了模糊遺傳算法進行熱布局優(yōu)化的有效性和優(yōu)越性,。

5 結論

    本文提出一種基于模糊遺傳算法的兩層埋入式電阻元件熱布局優(yōu)化方法，通過設計遺傳算法的適應度函數,、采用模糊邏輯控制規(guī)則自適應調整交叉概率和變異概率,，以及對長時間未進化的種群執(zhí)行局部災變等措施來保持種群多樣性并抑制早熟收斂,，使算法最終收斂于全局最優(yōu)解。與采用標準遺傳算法進行熱布局優(yōu)化的方法相比,，本文算法在保持種群多樣性及搜索全局最優(yōu)解方面具有明顯優(yōu)勢,，且ANSYS溫度場分布以及實驗樣件的熱成像結果顯示其最高溫度及最大溫差都有較大幅度降低。根據優(yōu)化結果獲得的兩層電子元件熱布局規(guī)則除適用于本文所研究的埋入式電阻,，對其他電子元件的熱布局設計也具有指導作用,。但是，由于遺傳算法本身具有較高的復雜度,，增加了模糊邏輯控制后計算復雜度進一步提高,，不利于實時性的實現(xiàn)。在今后的研究中,，將考慮融合優(yōu)化精度更高、速度更快的進化計算方法,，如粒子群算法和蟻群算法等應用到埋入式電子元件的熱布局設計中,。

參考文獻

[1] 閆德勁，周德儉,，黃春躍,，等.基于遺傳算法的表面組裝電子元件熱布局優(yōu)化[J].電子機械工程，2007,，23(2)：12-17.

[2] Huang Chunyue,，Li Tianming，Liang Ying,，et al.Study on thermal placement optimization of embedded MCM[C].Advanced Materials Research. Switzerland：Trans Tech Publications,，2011：2269-2273.

[3] 梁穎，黃春躍,，閻德勁,，等.基于熱疊加模型的疊層3D多芯片組件芯片熱布局優(yōu)化研究[J].電子學報，2009,，37(11)：2520-2524.

[4] 陳清遠,，容錦泉.埋入式電阻的熱特性研究[J].電子元件與材料，2005,，24(12)：61-63.

[5] LALL B S,，KABIR A.Thermal design rules for electronic components on conducting boards in passively cooled Enclosures[C].Proceedings of the 4th Intersociety Conference on Thermal Phenomena in Electronic Systems.New York，1994：50-61.

[6] 徐寧,，洪先龍,，陳松，等.熱約束的BBL布局算法研究[J].計算機輔助設計與圖形學學報,，2005,，117(16)：1312-1315.