0 引言

    物理層網(wǎng)絡(luò)編碼通過(guò)在中繼節(jié)點(diǎn)選擇適當(dāng)?shù)恼{(diào)制解調(diào)技術(shù),，將相互疊加的電磁波信號(hào)映射為相應(yīng)的數(shù)字比特流,，然后進(jìn)行異或處理（即進(jìn)行了網(wǎng)絡(luò)編碼），使得所有多徑,、多播干擾變成網(wǎng)絡(luò)編碼的一部分,，充分利用干擾來(lái)提高通信系統(tǒng)的性能^[1]。該技術(shù)自2006年提出以來(lái)就受到廣泛關(guān)注^[2],。

    在同步條件下將物理層網(wǎng)絡(luò)編碼應(yīng)用在無(wú)線中繼系統(tǒng)傳輸中,，可以使網(wǎng)絡(luò)吞吐量比直接網(wǎng)絡(luò)編碼模式和傳統(tǒng)中繼轉(zhuǎn)發(fā)模式分別提高50%和100%,，信號(hào)傳輸速率也分別提高50%和100%^[3]，此外系統(tǒng)的抗干擾能力和安全性能也得到了提高,。但在實(shí)際環(huán)境中,，由于信道的距離、類型不同,，以及不同終端之間振蕩器,、晶振頻率等不可能做到完全同步，造成中繼節(jié)點(diǎn)接收到的兩個(gè)源節(jié)點(diǎn)信號(hào)存在載波相位偏移,、載波頻率偏移以及符號(hào)偏移,，使得物理層網(wǎng)絡(luò)編碼的性能受到損失^[4-6]，因此研究各個(gè)因素對(duì)系統(tǒng)性能的影響具有重要意義,。

    文獻(xiàn)[7-9]從功率方面對(duì)系統(tǒng)性能損失進(jìn)行理論推導(dǎo)和仿真實(shí)驗(yàn),，分析了各種異步條件對(duì)功率的影響。然而各種異步條件對(duì)系統(tǒng)誤碼率的影響一直缺乏相關(guān)理論,。針對(duì)上述存在的問(wèn)題,，采用XOR的映射方式，在中繼節(jié)點(diǎn)采用不同的處理方式,，完成載波相位,、載波頻率偏移以及符號(hào)偏移對(duì)通信系統(tǒng)誤碼率的理論推導(dǎo)和仿真實(shí)驗(yàn)，為物理層網(wǎng)絡(luò)編碼的工程應(yīng)用奠定理論基礎(chǔ),。

1 系統(tǒng)模型

    本文考慮如圖1所示的雙向中繼系統(tǒng)模型^[10],，首先兩個(gè)源節(jié)點(diǎn)A和B同時(shí)向中繼節(jié)點(diǎn)R發(fā)送信息(即多址接入階段)，然后中繼節(jié)點(diǎn)R對(duì)兩個(gè)目的節(jié)點(diǎn)A和B(也就是源節(jié)點(diǎn))廣播信息,。

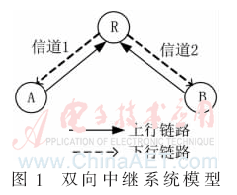
    在中繼節(jié)點(diǎn)處理疊加信號(hào)的方法主要有：基于符號(hào)的疊加（Superposition,，SUP）、基于排斥準(zhǔn)則的近鄰成簇（Closest-neighbor cluster,，CNC）映射^[9],、基于碼字的向量模加（Vector modulo addition,VMA）^[11]和基于比特的XOR等方法。其中基于比特的XOR方法最簡(jiǎn)單,、最實(shí)用^[12],，因此在中繼節(jié)點(diǎn)處采用XOR映射方式處理疊加信號(hào)。

2 影響因素及分析

2.1 載波相位的影響

    假設(shè)兩發(fā)送信號(hào)載波相位差為θ,，使用BPSK調(diào)制,，則兩源節(jié)點(diǎn)A和B發(fā)送的信號(hào)分別為：

    在中繼節(jié)點(diǎn)處對(duì)疊加信號(hào)乘以載波2cos(wt)，通過(guò)低通濾波器得到信號(hào)：

    在相位偏移的條件下,，物理層網(wǎng)絡(luò)編碼的映射關(guān)系如表1所示,。

    由表1可知：在中繼節(jié)點(diǎn)R處兩個(gè)端節(jié)點(diǎn)的和信號(hào)a_A+a_B經(jīng)過(guò)物理層網(wǎng)絡(luò)編碼映射之后分別得到-1和1，且-1和1的概率相等，均為50%,。根據(jù)上述條件可得：

式中f代表映射函數(shù),，由貝葉斯公式和條件概率公式可以推導(dǎo)出：

式中，N₀表示噪聲的方差,。通過(guò)式(8)可以得到物理層網(wǎng)絡(luò)編碼映射的判決門限r(nóng)₁和r₂,，從而推導(dǎo)出在載波相位偏移的條件下中繼節(jié)點(diǎn)接收信號(hào)的誤碼率公式：

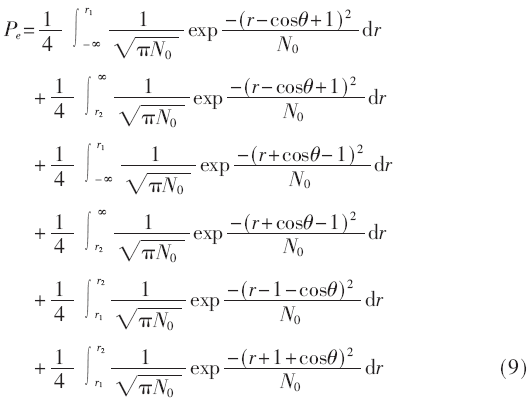
    圖2是相位偏移θ分別為0、π/5,、π/4和2π/5條件下信噪比隨誤碼率的變化曲線,。可以看出,，隨著載波相位偏移的增加,，信噪比對(duì)誤碼率的影響越來(lái)越小。

    角度θ和信噪比對(duì)誤碼率的影響如圖3所示,。在圖3的三維圖形中可以發(fā)現(xiàn),，當(dāng)載波相位偏移達(dá)到90°時(shí)，系統(tǒng)的誤碼率不再隨著信噪比的變化而變化,，而是趨于一個(gè)常數(shù),。因此，在物理層網(wǎng)絡(luò)編碼的工程應(yīng)用中應(yīng)盡量減少載波相位偏移,。

2.2 載波頻率的影響

    假設(shè)兩個(gè)發(fā)送信號(hào)載波頻率差為Δw,，則兩源節(jié)點(diǎn)A和B發(fā)送的信號(hào)分別為：

    從式(13)中得到，誤碼率和4個(gè)量有關(guān)系,，分別是判決門限r(nóng)₁和r₂,、載波頻率偏移Δw,、幀數(shù)k和采樣周期T,。一般情況下取T=1，則誤碼率由r₁,、r₂,、Δw和k決定。

    當(dāng)載波頻率偏移較小時(shí),，假定取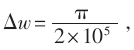則在SNR=5和SNR=10的條件下,，可以得到幀數(shù)k對(duì)系統(tǒng)誤碼率的影響，如圖4所示,。

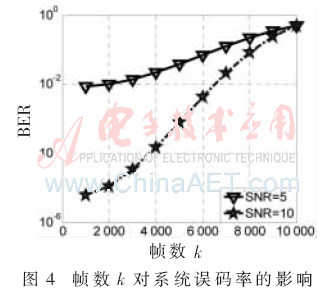
    通過(guò)圖4可以得到,，當(dāng)載波頻率偏移比較小的時(shí)候，隨著幀數(shù)的增加,，誤碼率逐漸提高,，而且趨于一個(gè)常數(shù)。因此，在載波頻率偏移比較小的條件下,，應(yīng)盡量減少幀數(shù),，以降低系統(tǒng)誤碼率。當(dāng)載波頻率偏移比較大的時(shí)候,，需要把Δw·k作為整體考慮,，將Δw·k的值整合到[0，π/2]之間,，其對(duì)系統(tǒng)的影響和載波相位偏移對(duì)系統(tǒng)的影響相似,。

2.3 符號(hào)偏移的影響

    假設(shè)兩個(gè)發(fā)送信號(hào)時(shí)間同步誤差為?Δt=εT(-1/2≤ε≤1/2)，則兩源節(jié)點(diǎn)A和B發(fā)送的信號(hào)分別為： 

    在中繼節(jié)點(diǎn)處對(duì)疊加信號(hào)乘以載波2cos(wt),，通過(guò)低通濾波器可以得到信號(hào)：

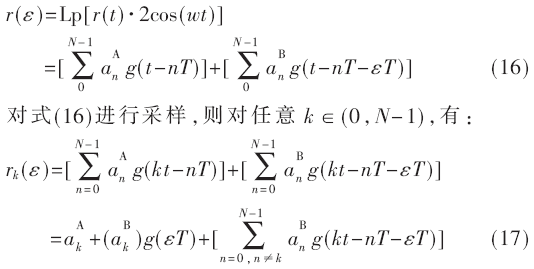
    由式(17)得到,，時(shí)間不同步在降低了信號(hào)功率的同時(shí)，還引來(lái)了符號(hào)間干擾,。

    為研究方便,，取脈沖成形函數(shù)為升余弦滾降函數(shù)，即：

    在有符號(hào)偏移的情況下,，物理層網(wǎng)絡(luò)編碼的映射關(guān)系如表2所示,。

    使用和載波相位偏移類似的方法，得到：

    類似地可以推導(dǎo)出在符號(hào)相位偏移的條件下中繼節(jié)點(diǎn)接收信號(hào)的誤碼率公式：

    圖5是符號(hào)偏移ε分別為0,、0.1,、0.3和0.5條件下，信噪比對(duì)誤碼率的變化曲線,?？梢缘玫剑涸谕恍旁氡认拢S著符號(hào)偏移的增加,，系統(tǒng)的誤碼率逐漸升高,。當(dāng)符號(hào)偏移為0.5個(gè)符號(hào)時(shí)，系統(tǒng)的誤碼率達(dá)到最高,，與同步條件(ε=0)下的誤碼率相比,，最大相差6 dB。

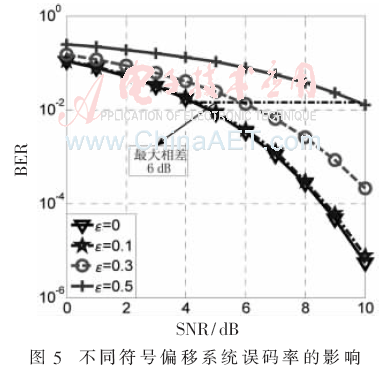
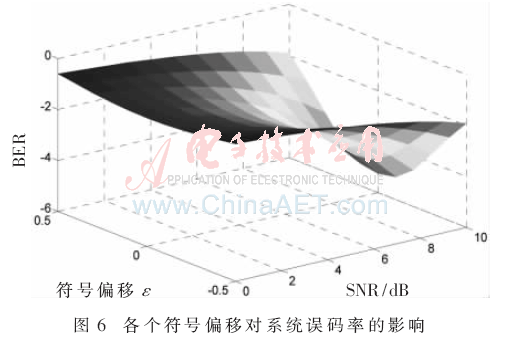
    圖6為符號(hào)偏移和信噪比的變化對(duì)誤碼率的影響結(jié)果,。由于g(t)是偶函數(shù),，因此圖像關(guān)于ε=0對(duì)稱。通過(guò)和圖3對(duì)比可知,，符號(hào)偏移對(duì)系統(tǒng)誤碼率的影響相對(duì)較小,。

3 結(jié)論

    本文采用XOR映射方式首次從理論上分別得到載波相位偏移、載波頻率偏移,、符號(hào)偏移與系統(tǒng)誤碼率的數(shù)學(xué)模型,。通過(guò)仿真實(shí)驗(yàn)可知,，在同一信噪比下，隨著載波相位偏移的增加,，系統(tǒng)的誤碼率逐漸增加,，當(dāng)相位偏移達(dá)到最大值90°時(shí)，系統(tǒng)的誤碼率趨于一個(gè)常數(shù),，不再隨信噪比變化,。在載波頻率偏移條件下，當(dāng)偏移較小時(shí),，幀長(zhǎng)的增加也會(huì)引起系統(tǒng)誤碼率的增加,，當(dāng)偏移較大時(shí)，系統(tǒng)性能受頻率偏差和幀長(zhǎng)共同作用,。隨著符號(hào)偏移的增加,，系統(tǒng)的誤碼率相對(duì)于同步條件下最大損失6 dB，相比于載波相位偏移損失較小,。本文通過(guò)理論推導(dǎo)和仿真實(shí)驗(yàn),，為后續(xù)的物理層網(wǎng)絡(luò)編碼工程誤差分析建立了理論參考基礎(chǔ)。

參考文獻(xiàn)

[1] Zhang Shengli,，Liew Soung Chang,，Patrick P.Lam.Physicallayer network coding[C].The Annual International Conference on Mobile Computing and Networking(ACM Mobi-Com).2006：358-365.

[2] 趙明峰，周亞建,，原泉,，等.物理層網(wǎng)絡(luò)編碼研究進(jìn)展[J].計(jì)算機(jī)應(yīng)用，2011,，31(8)：2015-2021.

[3] 陳志成.無(wú)線通信中物理層網(wǎng)絡(luò)編碼技術(shù)的研究[D].南京：南京郵電大學(xué),，2012.

[4] Lu Lu，Zhang Shengli.Asynchronous physical-layer network coding[J]．Wireless Communications,，IEEE Transactions,，2012，11(2)：819-831．

[5] Hao Yonggang,，Goeckel Dennis,，Ding Zhiguo,，et al.Achievable rates of physical layer network coding schemes on the exchange channel[C].Proceedings of 2007 IEEE Mil Comm Conf,，2007：1-7.

[6] Zhang Shengli，Liew Soung Chang,，Patrick P.Lam.On the synchronization of physical-layer network coding[C].Proceedings of 2006 IEEE Information Theory Workshop,，2006：404-408.

[7] Zhang Shengli，Liew Soung Chang,，Wang Hui.Synchronization analysis in physical-layer network coding[EB/OL].[2011-01-11].http：//arxiv.org/pdf/1001.0069.

[8] Zhang Shengli,，Liew Soung Chang,，Wang Hui.Synchronization analysis for wireless TWRC operated with physicallayer network coding[C].Wireless Pers Commun，2013(68)：637-653.

[9] 宋歡,，丁良輝,，錢良.基于無(wú)線幀的物理層網(wǎng)絡(luò)編碼同步誤差性能[J].信息技術(shù)，2013(9)：1-5.

[10] 苗金華.TWRC中物理層差分網(wǎng)絡(luò)編碼[D].天津：天津大學(xué),，2010.

[11] Nam Wooseok,，Chung SaeYoung，Yong H Lee.Capacity bounds for two-way relay channel[C].International Zurich Seminar on Communications(IZS),，2008：144-147.

[12] Popovski Petar,，Yomo Hiroyuki.Physical network coding in two-way wireless relay channels[C].IEEE International Conference on Communications，2007.