0 引言

    在電磁波被發(fā)現(xiàn)不久,，美籍科學家尼古拉·特斯拉便提出利用電磁波攜帶能量實現(xiàn)無線電能傳輸?shù)臉嬒?sup>[1]。無線電能傳輸分為電磁感應式、諧振耦合式和微波式^[2],。諧振耦合式較于電磁感應式的傳輸方式傳輸距離得到了極大的提高^[3],；較于微波式的傳輸方式只有幾毫瓦至幾百毫瓦的傳輸功率^[4]，耦合式幾十瓦甚至幾百瓦的傳輸功率更為有效,。諧振耦合式無線傳輸思想由MIT于2006年提出,，2007年MIT利用電磁諧振原理在2 m多的距離處點亮了60 W的燈泡，且傳輸效率達到了40%左右^[3],。

    目前諧振耦合式無線電能傳輸仍處于起步階段,，在傳輸距離、傳輸功率和傳輸效率這三大要素方面的分析還不夠^[5],。文獻[6]研究了傳輸功率,、傳輸效率與負載的關系并利用功效積對系統(tǒng)進行了優(yōu)化，但因忽略了接收線圈對發(fā)射線圈的影響導致最終理論與仿真結果懸殊較大,。文獻[7]考慮了接收線圈的影響,，但未考慮到系統(tǒng)傳輸效率較大時傳輸功率較低的情況。分析傳輸效率和功率與負載等因素之間的關系,，針對一些文獻為了計算方便忽略了接收線圈對發(fā)射線圈的影響造成較大誤差的問題,，對比得出了接收線圈的影響是不可忽略的結論。同時利用功效積指標使系統(tǒng)優(yōu)化解決了傳輸效率較大時往往功率不高的問題,，并且對模型及參數(shù)進行了仿真驗證,。

1 諧振耦合式無線電能傳輸系統(tǒng)原理與模型

1.1 諧振耦合式無線電能傳輸原理

    諧振耦合式無線電能傳輸系統(tǒng)原理性結構圖如圖1所示，包括發(fā)射端和接收端兩部分,。發(fā)射端由發(fā)射電路A和諧振線圈S組成,，接收端由諧振線圈D和負載電路B組成。

    系統(tǒng)工作時,，激勵線圈A產(chǎn)生高頻磁場,，源諧振線圈S在外加激勵下諧振，能量由A傳輸?shù)絊,，S通過磁諧振耦合將能量傳給次級諧振線圈D,，D再與負載電路B產(chǎn)生耦合將能量傳輸給負載。A,、S,、D、B 4個線圈均被設計成具有相同的諧振頻率,，在磁場的作用下可以產(chǎn)生諧振，但由于功能不同,，各個線圈的其他參數(shù)不盡相同,，如半徑等^[8]。

1.2 諧振耦合式無線電能傳輸電路模型

    為了分析的簡便,，僅對發(fā)生諧振耦合的兩收發(fā)線圈L_S,、L_D進行等效分析,，由于空心線圈在高頻下的寄生電阻和寄生電容不能忽略，因此L_S,、L_D的等效模型如圖2所示,。

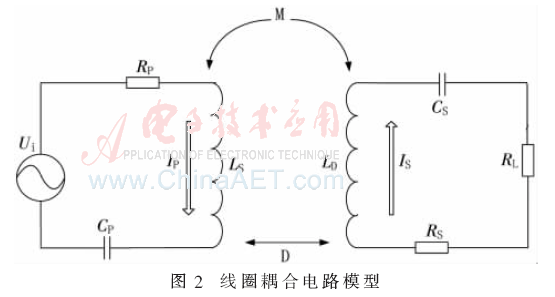
    圖2中，R_P,、R_S為發(fā)射線圈和接收線圈內(nèi)阻,，為計算方便近似取R_P≈R_S；C_P,、C_S為發(fā)射線圈和接收線圈補償電容,；U_i為加載在發(fā)射線圈上的激勵，其頻率為ω,；R_L為等效負載阻抗,；M為線圈互感。

1.3 諧振耦合式無線電能傳輸數(shù)學模型

    由于在傳輸過程中,，接收電路肯定會對發(fā)射電路產(chǎn)生一定的影響,，考慮這一因素后，根據(jù)圖1,，利用基爾霍夫定律可以寫出回路方程組：

    線圈傳輸效率是接收端負載上得到的功率和發(fā)射端的功率之比,，即：

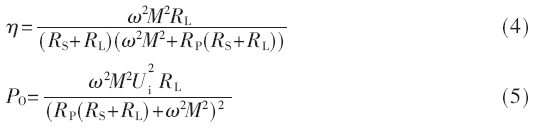
    可見傳輸效率與功率均與ω、M,、R_S,、R_P、R_L有關,。當收發(fā)線圈參數(shù)一致時（即K_S=K_D）時：

其中,，μ₀為真空磁導率， r為線圈半徑,， d為傳輸距離,，可見互感與 r、 n,、 d有關,。

    高頻下線圈損耗電阻主要包括歐姆損耗電阻R_O和輻射損耗電阻R_r^[9]：

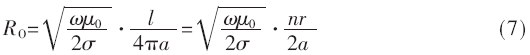
其中，a為導線半徑,；n為線圈匝數(shù),；σ為電導率；l為導線長度,。

    對于諧振耦合式無線電能傳輸系統(tǒng),，其諧振頻率一般為1 MHz~50 MHz，此時有Rr<<Ro^[9]，即可忽略輻射損耗,，則線圈損耗電阻R_p=R_s≈R_o,。

2 系統(tǒng)分析與優(yōu)化設計

2.1 系統(tǒng)最大功效積基本原理

    一個系統(tǒng)中傳輸效率和傳輸功率是分不開的，但是大部分情況下很難使效率和功率同時得到最大值,，于是引入功效積ψ這個概念,，即功率和效率的乘積，當功效積達到最大值時,，效率和功率均達到了較大值,。由式(4)、式(5)得：

2.2 功效積與傳輸效率對比分析

    隨著負載的變化,，效率存在最大值,，即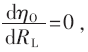求解可得：

    將式(12)代入式(4)和式(5)得(傳輸效率取最大)：

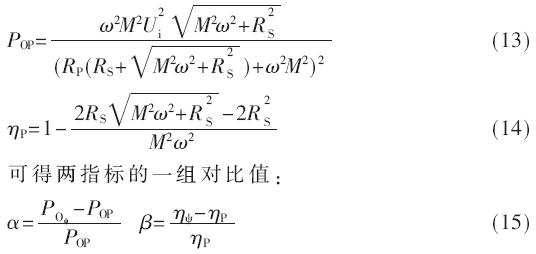
    假設等效模型參數(shù)如表1所示。

    根據(jù)表1的參數(shù)與式(10)～(11),、式(13)～(15)可得：α≈36%,，β≈-9%。由α,、β可知,，最大功效積傳輸與最大效率傳輸相比，雖然效率下降了9%,，但是功率上升了36%,。綜上所述，最大功效積相比較于最大效率傳輸具有優(yōu)越性,，對系統(tǒng)進行了優(yōu)化,，實現(xiàn)了較高傳輸效率的同時擁有較高的輸出功率。

2.3 與忽略接收線圈系統(tǒng)的對比分析

    一些文獻為了研究方便忽略了接收電路對發(fā)射電路的影響,，使理論推導進一步簡化,。

    根據(jù)文獻[7]中的公式與表1參數(shù)得：當忽略接收線路對發(fā)射線路影響時，最佳負載R_L≈13.3 Ω,。

    由式(9)得,，當考慮影響因素時，最佳負載R_L≈17.5 Ω,。

    對比上述兩種情況可得,，忽略接收線圈影響與不忽略影響的最佳負載誤差約為32%，誤差很大,，可證明接收電路對發(fā)射電路的影響不可忽略,。

3 仿真結果與分析

3.1 不忽略接收線圈影響的仿真分析

    由上文可知，功效積為最大時,，負載約為17.5 Ω,。運用MATLAB軟件對圖1仿真得出對應的輸出電流,、輸入電壓和輸入電流如圖3～圖5所示,。

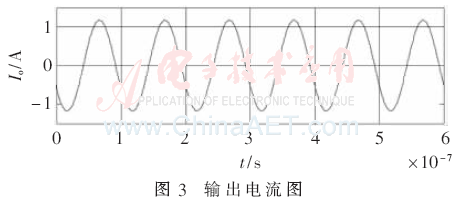
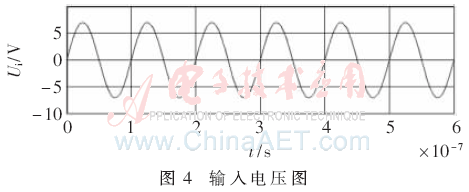
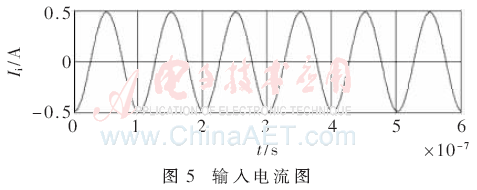
    當負載分別7.5 Ω,、12.5 Ω、17.5 Ω,、22.5 Ω,、27.5 Ω時，分別仿真得到對應的輸出功率,、效率和功效積,，再根據(jù)式(4)、(5),、(8)計算出對應的輸出功率,、效率和功效積，理論數(shù)據(jù)和仿真結果如表2所示,。

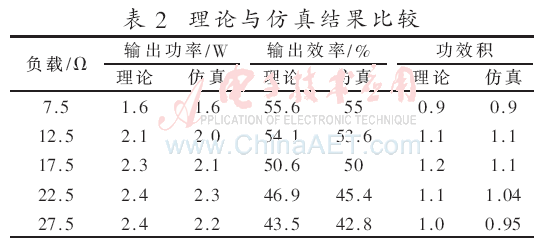
    由理論分析可知：負載為17.5 Ω時,，功效積達到最大。且由表2中幾組仿真數(shù)據(jù)對比可知,，當負載為17.5 Ω時,，功效積最大。從表2可以看出,，理論與仿真的結果基本吻合,，而且當功效積最大時，可以同時保證較高的輸出功率和效率,，從而論證了功效積的優(yōu)越性,。但是理論與仿真還是存在一定差距，是因為理論分析十分理想化并且忽略了線圈的輻射損耗電阻,，而且仿真過程中很多參數(shù)設置為近似數(shù)所導致的,。

3.2 忽略接收線圈影響的仿真分析

    當忽略接收電路對發(fā)射電路的影響，取負載13.3 Ω時,，運用MATLAB軟件可得仿真結果如圖6～圖8所示,。

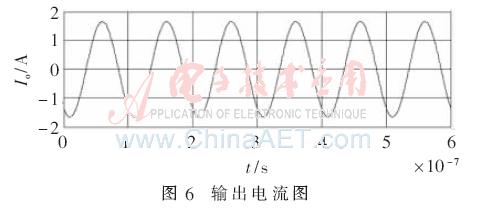
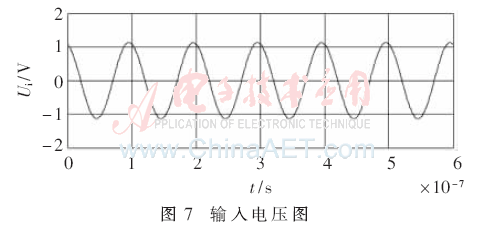
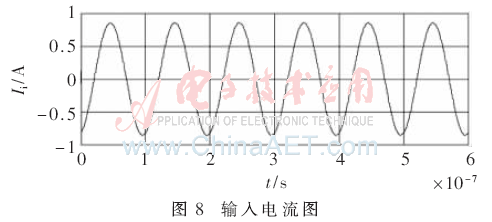
    由圖6～圖8可得仿真結果η_D=82%，P_D=4.8 W,。

    由表1的參數(shù)與式(14)得,，不忽略接收線圈影響的最大傳輸效率為55.7%，與η_D對比再次印證了接收線圈對發(fā)射線圈影響的不可忽略性,。

4 總結

    本文利用互感等效模型分析了影響輸出效率和功率的因素,。得出了以下結論：

    (1)忽略接收線圈的影響后，最佳負載的誤差達32%,，且傳輸效率仿真結果為82%,，遠高于理論最大值55.7%,，證明了接收線圈的影響是不可忽略的。

    (2)功效積為最大時的傳輸效率雖然比傳輸效率最大值低了9%,，但輸出功率卻比效率最大時上升了36%,，說明了功效積對系統(tǒng)確實進行了優(yōu)化。

    (3)仿真結果與理論數(shù)據(jù)誤差在3%左右,，而忽略接收線圈影響的誤差為32%,，說明了理論分析過程的優(yōu)越性。

參考文獻

[1] LI H L,，HU A P,，COVIC G A，et al.Optimal coupling condition of IPT system for achieving maximum power transfer[J].Electronics Letters,，2009,，45(1)：76-77.

[2] 黃靜，邵兵,，王劍飛.無線電能傳輸系統(tǒng)參數(shù)優(yōu)化[J].電子技術應用,，2014，40(12)：28-31.

[3] 汪強,，李宏.基于磁耦合諧振的無線電能傳輸系統(tǒng)的研究[J].電子技術應用,，2011，37(12)：72-75.

[4] YOUNDO T,，JONGMIN P,，SANGWOOK N.Mode-based analysis coupled of resonant characteristics for near-field small antennas[J].IEEE Antennas and Wireless Propagation Letters，2009(8)：1238-1241.

[5] JIN W K,，HYEON C S,，KWAN H K，et al.Efficiency analysis of magnetic resonance wirelesspower transfer with intermediate resonant coil[J].IEEE Antennas and Wireless Propagation Letters,，2011(10)：389-392.

[6] 張智娟,，董苗苗.諧振式無線電能傳輸系統(tǒng)的研究[J].電子技術應用，2013,，39(8)：54-56.

[7] 傅文珍,，張波，丘東元,，等.自諧振線圈耦合式電能無線傳輸?shù)淖畲笮史治雠c設計[J].中國電機工程學報,，2009，29(18)：21-26.

[8] 鄭盼龍,，遲冬祥.一種小型磁諧振式無線電能傳輸系統(tǒng)的實驗研究[J].機電工程,，2014，31(10)：1333-1338.

[9] KURS A,，KARALIS A.Wireless power transfer via strongly coupled magnetic resonances[J].Science,，2007,，112(6)：83-86.