0 引言

　　在無線傳感器網(wǎng)絡的關(guān)鍵支撐技術(shù)中[1],，定位技術(shù)是極其重要的組成部分，在其應用領(lǐng)域內(nèi),，事件發(fā)生的位置信息是傳感器節(jié)點監(jiān)測消息中的重要信息,，沒有節(jié)點位置信息的感知數(shù)據(jù)是毫無意義的[1]。

　　無線傳感器網(wǎng)絡的定位算法根據(jù)節(jié)點間的測距要求,，主要分為距離相關(guān)和距離無關(guān)兩大類[2],。典型的距離相關(guān)的測距算法主要有：RSSI,、TOA、TDOA,、AOA等,，分別利用三邊測量法、三角測量法,、極大似然估計法,、最小二乘法等來進行節(jié)點定位；典型的距離無關(guān)算法主要有：質(zhì)心算法,、DV-HOP,、MDS-MAP、APIT等,。為提高定位精度,，適宜采用距離相關(guān)的算法。在距離相關(guān)的幾種測距算法中,，通過表1可以看出：基于RSSI的定位算法具有成本低,、容易實現(xiàn)等優(yōu)點，在對定位精度不高的情況下得到了廣泛的應用,。另外,，目前很多傳感器節(jié)點都提供測量信號發(fā)射功率的功能，可以在節(jié)點廣播消息包的同時完成 RSSI 測量值的獲取,，并且這種定位算法無需額外的硬件支持和復雜的數(shù)據(jù)處理,，也不會增加通信開銷，能有效減少節(jié)點的硬件成本和能量消耗,，適用于無線傳感器網(wǎng)絡,。

　　近十年來，WSN獲得快速發(fā)展,，人們研究的對象不僅僅針對靜態(tài)WSN,，而且漸漸地關(guān)注動態(tài)網(wǎng)絡的節(jié)點定位技術(shù)，這樣的要求就使得靜態(tài)定位算法在移動環(huán)境下就變得無效了,。經(jīng)典的WSN移動節(jié)點定位算法主要有：MCL[3],、MCB[4]、MSL和MSL*[5],、MMCL[6],、rang-based-MCL[7]、RSS-MCL[8],、OTMCL[9]等,。

　　弗吉尼亞大學的Hu和Evans首次提出了將蒙特卡洛定位算法應用于移動無線傳感網(wǎng)絡節(jié)點定位中[3]，其提高了定位精度，減少了定位開銷,；針對MCL采樣效率低的問題Baggio A和Langendoen K提出了蒙特卡洛盒子定位（Monte Carlo Localization Boxed,，MCB）算法[4]；約克大學的Rudafshani M和Datta S提出了移動和靜態(tài)傳感網(wǎng)絡定位算法MSL和MSL*算法[5],；Dil B提出的Range-based-MCL[7]算法為基于距離的移動WSN定位,，通過利用未知節(jié)點與錨節(jié)點之間的距離信息，可以濾波得到更精確的位置樣本,，提高了定位精度,。特別需要指出的是，Wang[8]等人將MCL和RSSI定位算法相結(jié)合,，提出了基于RSSI的MCL定位算法,，利用接收信號強度的對數(shù)正態(tài)模型對定位的預測和濾波過程進行了改進，改善了定位性能,。

　　上述算法中,，基于RSSI的MCL定位算法效果良好，在定位技術(shù)的研究和實際運用方面都有很大的意義,，但存在計算量較大,、無運動預測性等不足。因此,，本文在文獻[3]和文獻[8]的基礎(chǔ)上,，對移動無線傳感器網(wǎng)絡節(jié)點定位進行了深入研究，提出了一種基于RSSI的改進蒙特卡羅定位算法RSSI-IMCL,。事實上，節(jié)點在運動過程中的運動參數(shù)一般不會突變,，且基于RSSI的MCL算法沒有考慮運動預測問題,，因而可以利用前幾個時刻的軌跡，預測當前時刻的運動參數(shù),，減小采樣范圍,，提高采樣準確率，從而提高定位精度,，降低節(jié)點功耗,。

1 基于RSSI的改進MCL算法

　　本文提出的算法是對基于RSSI的蒙特卡洛算法的一種改進，基本思想與經(jīng)典MCL和基于RSSI的MCL算法相似,。即首先建立與描述該問題有相似性的概率模型,，然后對模型進行隨機模擬或統(tǒng)計抽樣，再利用所得的結(jié)果求出特征量的統(tǒng)計值作為原問題的近似解,，并對解的精度作出某些估計,。

　　1.1 RSSI模型

　　一般的RSSI通信模型都認為網(wǎng)絡中各節(jié)點為各向同性，例如自由空間傳播模型、雙射線模型,、哈他模型等皆為各向同性,，這類模型皆是按照式（1）的框架建立的模型。

　　接收信號強度=發(fā)送功率-路徑損耗+信號衰退(1)

　　自由空間傳播是電波在真空中無阻擋視距傳播的一種理想狀態(tài),。其模型可以表示為式（2）：

　　[Lfs]=32.44-10klgd+10klgf(2)

　　式(2)中,，Lfs為傳輸損耗，d為節(jié)點距離,，k為路徑衰減因子,，一般取值為2，頻率單位以MHz計算,。

　　在實際傳輸過程中,，多徑現(xiàn)象不可避免，信號在傳輸時可能被一些障礙物吸收,，或是發(fā)生反射,、散射或衍射。這時我們可以采用不規(guī)則無線電模型來模擬實際應用環(huán)境,，該模型在不同方向的路徑損耗是不同的,。圖1表示的是自由模型和不規(guī)則電模型下RSSI值的比較。不規(guī)則電模型公式為式（3）：

　　式(3)中,，Pr(d)為接收功率,，Pt為發(fā)送功率，PL(d0)為參考距離時的路徑損耗,。

　　1.2 基于RSSI的MCL算法

　　蒙特卡洛定位其實就是一個粒子濾波算法,，每一個定位時刻都被分為了預測和更新兩部分。在預測階段,，根據(jù)節(jié)點速度信息和在上一定位時刻的粒子集確定采樣區(qū)域,，并隨機采樣得到粒子；在濾波階段,，根據(jù)收到的錨節(jié)點信息,，對預測階段的粒子進行篩選，濾除不符合觀測條件的,，并用滿足濾波條件的粒子的均值來估計節(jié)點的位置,，如果濾波得到的粒子數(shù)沒有達到定位所需的粒子數(shù)，則執(zhí)行重采樣和濾波過程,，直到得到足夠數(shù)量的粒子或者達到最大采樣次數(shù)為止,。

　　以下三個步驟詳細說明了基于RSSI的MCL算法的定位過程。假設(shè)整個無線網(wǎng)絡中,，有一個未知的移動節(jié)點和M個位置已知的錨節(jié)點隨機分布在整個區(qū)域中,。

　?。?）預測階段

　　在預測階段，傳感器節(jié)點需要根據(jù)前一時刻的粒子集Lt-1和運動模型確定當前時刻的粒子集Lt,。假設(shè)節(jié)點按照隨機行走模型（RWP）進行移動,，該模型中，節(jié)點在任何時刻都不知道自己的運動速度和方向,，僅僅知道自身的最大運動速率為vmax,，方向為360°任意選擇。那么轉(zhuǎn)移分布p(mk|mk-1)便形成了一個以mk-1為圓心,，以vmax為半徑的圓,。表示如式（4）

　　在MCL算法的預測階段，基于前一時刻位置對當前時刻位置進行預測,，節(jié)點可能的位置從上述的圓形區(qū)域隨機采樣獲得,，該圓形區(qū)域就是采樣區(qū)域。

　?。?）濾波階段

　　在濾波階段,，節(jié)點將根據(jù)新的觀測信息，將不符合網(wǎng)絡連通度條件的位置樣本濾除掉,。如果樣本滿足濾波條件,，則概率分布為1，否則為0,。如果滿足濾波條件的粒子數(shù)達到了定位所需數(shù)量,，則將這些粒子取均值作為節(jié)點的估計位置；如果粒子數(shù)不足,，則重復預測和濾波過程,，直到得到足夠數(shù)量的粒子或達到最大采樣次數(shù)為止。在MCL算法中,，為方便計算,，選擇狀態(tài)轉(zhuǎn)移概率密度函數(shù)為重要性函數(shù)，則每一時刻粒子的重要性權(quán)值可通過下列方法遞歸計算：

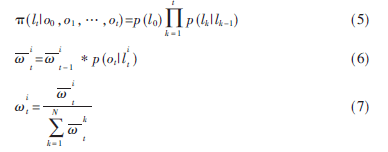
　　式(5)為預測階段,，節(jié)點可以在前一時刻可能位置的基礎(chǔ)上預測當前時刻的可能位置。式(6)為更新階段,，節(jié)點可以根據(jù)接收到的觀測信息更新當前時刻的粒子權(quán)值,。然后用式(7)對權(quán)值進行歸一化，從而可以用一組帶權(quán)值的樣本集來估計節(jié)點位置的后驗概率分布,。

　?。?）重采樣階段

　　計算當前的位置需要重復進行預測和更新，將不可避免地出現(xiàn)粒子退化現(xiàn)象,。因此需要重采樣,，將權(quán)重值小的樣本淘汰，將權(quán)重值大的保留，用式（8）定義有效粒子數(shù)Neff,，當Neff小于設(shè)定的門限值Nthreshold時,，就需要進行重采樣。

　　基于RSSI的MCL算法相比于經(jīng)典的MCL算法,，較大幅度地提高了定位精度,，取得了良好的效果，但計算量較大,，節(jié)點功耗過快,，需要改進。

　　1.3 基于RSSI的改進MCL算法

　　針對基于RSSI的MCL算法的不足,，本文提出了一種基于RSSI的改進MCL算法,。在基于RSSI的MCL算法的預測階段，k時刻的位置概率分布只與k-1時刻的位置及速度有關(guān),，沒有考慮k-1時刻之前的運動情況的影響,，本文采用基于歷史軌跡的運動預測機制來提高先驗概率的準確性，也就是意味著可能更高的定位精度和可能更少的迭代次數(shù),，從而降低節(jié)點的功耗,。

　　Newton插值法和Lagrange插值法雖然構(gòu)造比較簡單，但是存在插值曲線在節(jié)點處有尖點,、不光滑,、插值多項式在節(jié)點處不可導等缺點，因此本文選擇Hermite插值法,。一般,，Hermite插值多項式Hk(x)的次數(shù)k如果太高會影響收斂性和穩(wěn)定性稱為runge現(xiàn)象。本文中,，就采用前兩個時刻的位置信息,，因此不會出現(xiàn)runge現(xiàn)象。

　　設(shè)f(x)在節(jié)點x0,、x1處的函數(shù)值為y0,、y1，在節(jié)點x0,、x1處的一階導數(shù)值為,，兩個節(jié)點最高可用3次Hermite多項式H3(x)作為插值函數(shù)。H3(x)應滿足的插值條件為H3(x0)=y0,、H3(x1)=y1,、設(shè)H3(x)的插值基函數(shù)H3(x)=a0 h0(x)+a1 h1(x)+a2 h2(x)+a3 h3(x)，即H3(x)=ai hi(x),。

　　希望該函數(shù)與Lagrange和Newton插值一樣簡單,，重新假設(shè)：

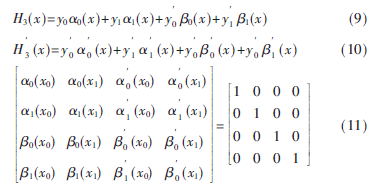
　　由上式(11)中的 (x1)=0可知,，x1是(x)的二重零點，可設(shè)(x)=(x-x1)2(ax+b),，由(x0)=1,、(x0)=0可知：

　　繼而可得?琢0(x)。

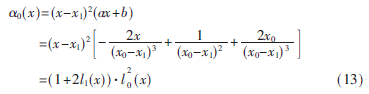
　　類似可得

　　將式(13),、(14),、(15)、(16)代入H3(x)=a0 h0(x)+a1 h1(x)+a2 h2(x)+a3 h3(x)中,，得：

　　在算法預測階段,，利用歷史軌跡，提高了當前位置預測的準確性,，減小了采樣范圍,，提高了采樣準確率，從而降低節(jié)點功耗,。

2 仿真分析

　　仿真實驗使用MATLAB進行,，該仿真實驗是在一個14 m×10 m的矩形平面區(qū)域進行的。信標節(jié)點隨機地分布在平面區(qū)域內(nèi),，其位置是固定不變的且坐標是已知的,；未知節(jié)點方向和速度大小都隨機移動，且其移動速度不會超過設(shè)定的最大速度,。網(wǎng)絡中使用的參數(shù)設(shè)定如下：節(jié)點的最大移動速度取10 m/s,，信標節(jié)點和未知節(jié)點的通信半徑相等且都取3 m。

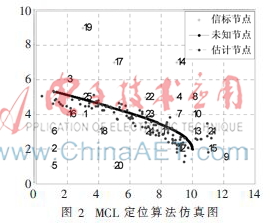
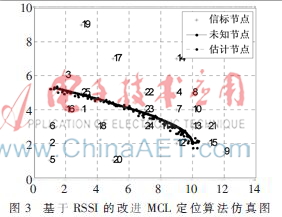
　　圖2和3顯示的是MCL定位算法和基于RSSI改進的定位算法的定位仿真圖,，可以看出,，改進的算法定位的軌跡更接近實際軌跡，定位精度有明顯的提高,。

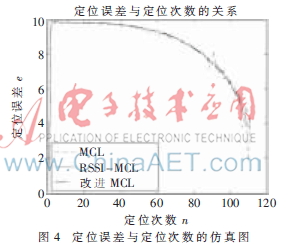
　　定位誤差用于描述定位結(jié)果的精確程度,，本文用到的定位誤差的定義如下：

　　其中，(xi,，yi)為未知節(jié)點的實際位置,，(x，y)為用算法估計出來的坐標位置,。如圖4可知,，隨著時間的推移，定位次數(shù)的增加,，定位誤差也在減小。

3 結(jié)論

　　本文對基于RSSI的蒙特卡洛無線傳感定位算法進行了深入研究,，并在此基礎(chǔ)上提出了一種基于RSSI的改進蒙特卡洛定位算法,。該算法在定位精度,、計算量、對錨節(jié)點密度的要求和對粒子樣本集的要求等性能都有所提升,，且通過仿真實驗證明該算法在移動的WSN中是一個高效的定位算法,。

參考文獻

　　[1] 馮硯毫，曾孝平,，江禹生.無線傳感器網(wǎng)絡節(jié)點定位技術(shù)研究[D].重慶：重慶大學,，2011.

　　[2] 黃俊霖，楊剛.基于RSSI分級的WSN節(jié)點定位算法研究[D].西安：西安電子科技大學.2013.

　　[3] Hu Lingxuan,，EVANS D.Localization for mobile sensor networks[C].Proc of the 10th Annual International Confer-ence on Mobile Computing and Networking(Mobicom04),，Philadelphia，Pennsylvania：USA,，2004：45-57.

　　[4] BAGGIO A,，LANGENDOER K.Monte carlo iocalization for mobile wireless sensor networks[C].Proceedings of the 2nd =International Conference on Mobile Ad-hoc and Sensor Networks(MSN′06)，Dec 13-15,，2006,，Hong Kong，China.LNCS 4325.Berlin,，Germany：Springer-Verlag,，2006：718-733.

　　[5] RUDAFSHANI M，DATTA S.Localization in wireless sensor networks[C].Information Processing in Sensor Networks,，2007.IPSN 2007.6th International Symposium on,，pp.51，60,，25-27 April 2007.

　　[6] Yi Jiyoung,，Won YangSung，Cha Hojung.Multi-hop-based Monte Carlo Localization for Mobile Sensor Networks[C].Proceedings of The 4th Annual IEEE Communications Society Conference on Sensor,，Mesh and Ad Hoc Commun-ications and Networks,，San Diego，California,，USA,，2007：163-171.

　　[7] DIL B，DULMAN S,，HAVINGA P.Range-based localizationin mobile sensor networks[J].Wireless Sensor Networks,，2006：164-179.

　　[8] WANG W D，ZHU Q X.RSS-based Monte Carlo localiza-tion for mobile sensor networks[J].Communications,，IET,，2008，2(5)：673-681.

　　[9] MARTINS M H T,，CHEN H,，SEZAKI K.OTMCL：Orienta-tion tracking-based Monte Carlo localization for mobile sensor networks[C].Proceedings of the 6th International Con-ference on Networked Sensing Systems (INSS),，2009：1-8.

　　[10] 李偉，丁勇,，于春娣,，等.一種基于RSSI的改進蒙特卡羅定位算法[J].計算機應用與軟件，2013(12)：280-283.