摘  要： 對(duì)ISOMap,、LDA、LLE,、PCA這4種典型降維算法的主要思想和算法步驟進(jìn)行了詳細(xì)分析,，并將它們用于有監(jiān)督分類。從實(shí)驗(yàn)結(jié)果分析得到結(jié)論,，其可為有監(jiān)督分類提供有益的借鑒,。

關(guān)鍵詞： 維數(shù)約簡；監(jiān)督分類,；樣本外點(diǎn)問題

0 引言

　　隨著信息技術(shù)和空間技術(shù)的快速發(fā)展,，人類每天都可以獲得海量的數(shù)據(jù)，很多數(shù)據(jù)往往都是高維的,，例如生物基因序列分析,、高光譜遙感圖像處理等領(lǐng)域所要處理的數(shù)據(jù)。而高維數(shù)據(jù)難以被人理解,、表示和處理[1]，降維是解決問題的一個(gè)可行途徑,。近年來,，降維已經(jīng)成為信息處理領(lǐng)域的一個(gè)研究熱點(diǎn)。

　　在高維數(shù)據(jù)降維方面,，目前使用的降維方法可分兩大類：線性降維和非線性降維,。比較有代表性的線性降維方法有：投影尋蹤（Projection Pursuit，PP）[2],、主成分分析（Principal Component Analysis,，PCA）[3]、多維尺度變化（MultiDimensional Scaling,，MDS）[4],、獨(dú)立成分分析（Independent Component Analysis，ICA）[5],、線性判別分析（Linear Discriminant Analysis,，LDA）[6]、邊際Fisher分析（Marginal Fisher Analysis,，MFA）[7],、無監(jiān)督判別映射（Unsupervised Discriminant Projection，UDP）[8]等,。常見的非線性降維方法包括：局部線性嵌入（Locally linear Embedding,，LLE）[9],、等距映射（Isometric Mapping，ISOMap）[10],、黎曼流形學(xué)習(xí)（Riemannian Manifold Learning,，RML）[11]、多流形（Multiple Manifolds,，MM）[12],、層次流形學(xué)習(xí)（Hierarchical Manifold Learning，HML）[13]等,。

1 典型線性降維算法

　　1.1 LDA

　　LDA的基本思想是利用樣本的類別標(biāo)簽信息,，通過對(duì)樣本集（X1，X2,，…,，Xk，…,，XN）的總類內(nèi)散布矩陣和總類間散布矩陣這兩個(gè)帶有類標(biāo)簽信息的統(tǒng)計(jì)量計(jì)算廣義特征值,，得到相應(yīng)的映射矩陣，最后通過映射矩陣將樣本從高維空間映射到低維空間,。LDA算法的核心是廣義特征值分解,。不妨用N表示訓(xùn)練樣本總數(shù)，num為類別總數(shù),，第k類樣本的樣本總數(shù)為Nk,，Xk表示第k類訓(xùn)練樣本特征向量的均值，X表示所有訓(xùn)練樣本特征向量的均值,，X（k）j表示第k類中的第j個(gè)樣本,，LDA的計(jì)算步驟如下[6]：

　　（1）計(jì)算第k類樣本的協(xié)方差矩陣：

　　變化矩陣W的d個(gè)列向量由廣義特征方程最大的d個(gè)廣義特征值λ1≥λ2≥…≥λd所對(duì)應(yīng)的廣義特征向量w1,，w2,，…，wd組成,，即W=[w1,，w2，…,，wd],。

　　（5）根據(jù)公式Y(jié)n=（W*）TXn,，計(jì)算出訓(xùn)練樣本Xn的低維嵌入Yn,，其中T表示矩陣的轉(zhuǎn)置，1≤n≤N。

　　1.2 PCA

　　PCA在標(biāo)準(zhǔn)正交變換的基礎(chǔ)上進(jìn)行降維,，基本思想是對(duì)樣本的散布矩陣進(jìn)行特征值分解,。用N表示訓(xùn)練樣本的總數(shù)，訓(xùn)練樣本為（X1,，X2,，…，Xk,，…,，XN），映射變化后的低維嵌入維數(shù)為d,，PCA算法的主要步驟如下[3]：

　?。?）計(jì)算所有訓(xùn)練樣本的均值向量：

　　（2）計(jì)算所有訓(xùn)練樣本的協(xié)方差矩陣W：

　?。?）計(jì)算協(xié)方差矩陣W的特征值和特征向量,，并對(duì)特征值從大到小排序；

　?。?）選擇最大的d個(gè)特征值λ1≥λ2≥…≥λd對(duì)應(yīng)的特征向量w1,，w2，…,，wd組成變換矩陣W*,，即W*=[w1，w2,，…,，wd]，根據(jù)公式Y(jié)n=（W*）TXn,，計(jì)算出訓(xùn)練樣本Xn的低維嵌入Yn,，其中1≤n≤N,。

　　2 典型非線性降維算法

　　2.1 ISOMap

　　ISOMap算法的基本思想是離得很近的兩個(gè)點(diǎn)之間的測地線距離用歐氏距離來代替,，離得較遠(yuǎn)的兩個(gè)點(diǎn)之間的測地線距離用最短路徑距離來代替，然后用經(jīng)典的MDS算法計(jì)算出低維嵌入坐標(biāo),。ISOMap算法的主要步驟如下[10]：

　?。?）構(gòu)造局部鄰域。用N表示訓(xùn)練樣本總數(shù),，對(duì)數(shù)據(jù)集X={x1,，x2，…,，xN}計(jì)算任意兩個(gè)樣本點(diǎn)xi和xj之間的歐式距離dx（xi,，xj），為每個(gè)樣本點(diǎn)尋找出k個(gè)近鄰點(diǎn)，將互為近鄰的樣本點(diǎn)用線段連接起來得到鄰接圖G,。

　?。?）計(jì)算最短距離。在圖G中,，設(shè)任意兩個(gè)樣本點(diǎn)xi和xj之間的最短距離為dG（xi,，xj）。若xi和xj之間存在連線,，則dG（xi,，xj）的初始值為dx（xi，xj）,，否則令dG（xi,，xj）=∞。對(duì)所有的k=1,，2,，…，N,，根據(jù)dG（xi,，xj）=min{dG（xi，xj）,，dG（xi,，xk）+dG（xk，xj）},，計(jì)算出最短距離dG（xi,，xj），最后得到距離矩陣DG={dG（xi,，xj）},。

　　（3）應(yīng)用經(jīng)典的MDS算法計(jì)算出低維嵌入,。

　　2.2 LLE

　　LLE算法的基本思想是流形在很小的局部鄰域上可以看成局部線性的,，可將每個(gè)高維數(shù)據(jù)點(diǎn)用若干個(gè)近鄰點(diǎn)的線性組合來近似表示，通過計(jì)算重構(gòu)權(quán)值矩陣進(jìn)行降維,，將高維流形上的近鄰點(diǎn)映射到低維空間,。LLE算法的主要計(jì)算步驟如下[9]：

　　（1）尋找每個(gè)樣本點(diǎn)的k個(gè)近鄰點(diǎn),。

　?。?）定義重構(gòu)誤差min（W）=（xp-wjpxpj）2，其中N表示訓(xùn)練樣本總數(shù),，xpj表示樣本點(diǎn)xp的第j個(gè)近鄰點(diǎn),，wjp表示重構(gòu)權(quán)值,，同一個(gè)樣本點(diǎn)xj的k個(gè)近鄰的重構(gòu)權(quán)值的和滿足wjp=1。根據(jù)重構(gòu)誤差最小原則,，利用最小二乘法計(jì)算出重構(gòu)權(quán)值矩陣W,。

　　（3）根據(jù)重構(gòu)權(quán)值矩陣W,，計(jì)算矩陣M=（I-W）T（I-W）的特征值和特征向量,，其中I表示單位矩陣。將特征值從小到大排列,，通常取最小的d個(gè)非零特征值對(duì)應(yīng)的特征向量作為LLE最終的低維嵌入,。

3 實(shí)驗(yàn)

　　3.1 數(shù)據(jù)數(shù)據(jù)與評(píng)價(jià)策略

　　為了對(duì)比上述4種降維方法的分類性能，采用參考文獻(xiàn)[14]中的遙感影像SPOT 5進(jìn)行分類實(shí)驗(yàn),，影像原圖和分類參考圖如圖1所示,。實(shí)驗(yàn)中選取了4類土地覆蓋類型進(jìn)行分類，分類前先對(duì)SPOT 5影像進(jìn)行多尺度分割,。參考文獻(xiàn)[15]計(jì)算出81維特征,。在實(shí)驗(yàn)區(qū)域中隨機(jī)選取對(duì)象，其中農(nóng)村宅基地選取了32個(gè)對(duì)象,，河流選取了28個(gè)對(duì)象,，灌溉水田選取了56個(gè)對(duì)象，養(yǎng)殖水面選取了72個(gè)對(duì)象,。通過2折交叉驗(yàn)證比較4種降維算法的分類性能,。

　　ISOMap、LDA,、LLE,、PCA這4種降維算法只是對(duì)訓(xùn)練樣本的高維特征進(jìn)行降維，對(duì)于測試樣本的低維嵌入應(yīng)該如何計(jì)算,，并沒有提供有效的解決途徑,。對(duì)于LDA和PCA，本文采用在訓(xùn)練樣本的基礎(chǔ)上計(jì)算得到的映射矩陣計(jì)算測試樣本的低維嵌入,；對(duì)于ISOMap和LLE,，采用流形學(xué)習(xí)中經(jīng)典的Non-parametric mapping[16]計(jì)算測試樣本的低維嵌入。實(shí)驗(yàn)中所采用的分類器為1NN,，并根據(jù)總體精度（Overall Accuracy,，OA）對(duì)算法的分類性能進(jìn)行評(píng)估,，OA的計(jì)算公式如下：

　　其中,，N表示訓(xùn)練樣本的總數(shù)，mkk表示第k類訓(xùn)練樣本中正確分類的個(gè)數(shù),，num表示訓(xùn)練樣本的類別總數(shù),。

　　3.2 實(shí)驗(yàn)結(jié)果與分析

　　在ISOMap,、LDA、LLE,、PCA這4種算法的分類實(shí)驗(yàn)中,，降維后的特征維數(shù)分別取2、5,、8,、10、15,、20,、25、30,，取這8個(gè)結(jié)果的平均值作為相應(yīng)算法在區(qū)間[2,，30]的平均分類精度。由于近鄰個(gè)數(shù)對(duì)ISOMap,、LLE算法的分類性能有較大影響,，在ISOMap、LLE的實(shí)驗(yàn)中重點(diǎn)對(duì)比了不同的近鄰個(gè)數(shù)2,、4,、6、8,、10,、12對(duì)算法性能的影響。對(duì)LDA和PCA而言,，由于不存在近鄰個(gè)數(shù),，因此在LDA和PCA的分類實(shí)驗(yàn)中重點(diǎn)對(duì)比了不同歸一化方式對(duì)算法分類性能的影響。4種算法的分類結(jié)果如圖2所示,。

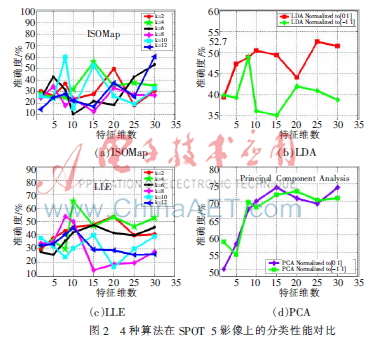
　　ISOMap不同近鄰個(gè)數(shù)得到的分類精度如圖2（a）所示,。當(dāng)近鄰個(gè)數(shù)取4時(shí)ISOMap的平均OA最高為33.85%，近鄰個(gè)數(shù)取4時(shí)的最高OA為55.32%,。

　　LDA不同歸一化方式得到的分類結(jié)果如圖2（b）所示,。當(dāng)LDA歸一化到區(qū)間[0，1]時(shí)得到的平均OA為48.01%,，最高OA為52.7%,；而當(dāng)LDA歸一化到[-1，1]區(qū)間時(shí)平均OA為40.16%,，最高OA為48.94%,。很明顯，當(dāng)LDA歸一化到[0,，1]區(qū)間時(shí)分類性能會(huì)更好一些,。

　　LLE不同近鄰個(gè)數(shù)得到的分類精度如圖2（c）所示,，當(dāng)近鄰個(gè)數(shù)取4時(shí)LLE的平均OA最高為45.22%，近鄰個(gè)數(shù)取4時(shí)的最高OA為64.9%,。

　　PCA算法不同的歸一化方式得到的分類精度如圖2（d）所示,。當(dāng)高維特征歸一化到[0，1]區(qū)間時(shí),，PCA的平均OA為66.59%,，最高OA為73.99%；而當(dāng)歸一化到 [-1,，1]區(qū)間時(shí),，PCA的平均OA為66.96%，最高OA為72.87%,?？梢钥闯觯瑹o論是平均OA還是最高OA,，兩種歸一化方式對(duì)PCA的分類結(jié)果影響并不大,。

　　可以看出，就平均OA而言,，PCA的分類性能最好,，ISOMap算法的OA最低，4種降維算法的平均OA均達(dá)不到70%,，換句話說,，ISOMap、LDA,、LLE,、PCA這4種算法直接用于監(jiān)督分類的效果并不好。分析其中的原因,，一方面是因?yàn)樵诮稻S過程中樣本的類別標(biāo)簽信息并沒有得到充分利用,，計(jì)算得到的低維嵌入與分類并沒有密切的聯(lián)系；另一方面是因?yàn)?種降維算法并沒有提供一種有效途徑來解決樣本外點(diǎn)學(xué)習(xí)問題,。

4 結(jié)論

　　本文詳細(xì)分析了ISOMap,、LDA、LLE,、PCA這4種降維算法的主要思想和算法步驟并將它們用于有監(jiān)督分類,。在降維過程中，樣本的類別標(biāo)簽信息是否得到充分利用會(huì)在很大程度上影響到低維嵌入的可區(qū)分性,。另一方面,，樣本外點(diǎn)學(xué)習(xí)問題是降維方法用于有監(jiān)督分類時(shí)必須要妥善解決的一個(gè)問題，該問題能否很好解決將在很大程度上影響到降維方法在有監(jiān)督分類中的應(yīng)用,。

　　參考文獻(xiàn)

　　[1] ANIL K J,， ROBERT P W  D， Mao Jianchang. Statistical pattern recognition： a review[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,， 2000,，21（1）：4-37.

　　[2] HUBER P J. Projection pursuit[J]. Annals of Statistics， 1985,， 13（2）： 435-475.

　　[3] JOLLIFFE I T. Principle component analysis[M]. Springer,， 1986.

　　[4] THOMAS L G， MICHAEL L K. A multidimensional scaling approach to mental multiplication [J]. Memory & Congnition,， 2002,， 30（1）：97-106.

　　[5] COMON P. Independent component analysis： a new concept[J]. Signal Processing， 1994,， 36（3）：287-314.

　　[6] FUKUNNAGA K. Intoduction to statistical pattern recogni-tion[M]. Academic Press,， second edition， 1991.

　　[7] Yan Shuicheng,， Xu Dong,， Zhang Benyu， et al. Graph embedding and extensions：a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,， 2007,， 29（1）：40-51.

　　[8] Yang Jian， ZHANG D. Globally maximizing,， locally minimizing： unsupervised discriminant projection with applications to face and palm biometrics[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,， 2007，29（4）： 650-664.

　　[9] ROWEIS S,， SAUL L. Nonlinear dimensionality reduction by locally linear embedding[J]. Science,， 2000， 290：2323-2326.

　　[10] TENENBAUM J B,， SILVA V,， LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science， 2000,， 290：2319-2323.

　　[11] Lin Tong,， Zha Hongbin. Riemannian manifold learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2008,，30（5）：796-809.

　　[12] Xiao Rui,， Zhao Qijun， ZHANG D,， et al. Facial expression recognition on multiple manifolds [J]. Pattern Recognition,， 2011， 44 （1）：107-116.

　　[13] Huang Hongbing,， Hong Huo,， Fang Tao. Hierarchical manifold learning with applications to supervised classification for high resolution remotely sensed images[J]. IEEE Transactions on Geoscience and Remote Sensing,，2014，52（3）：1677-1692.

　　[14] Qing Jianjun,， Huo Hong,， Fang Tao. Supervised classification of multispectral remote sensing images based on the nearest reduced convex hull approach[J]. Journal of Applied Remote Sensing， 2009（3）：1-18.

　　[15] Chen Xi,， Fang Tao,， Huo Hong， et al. Graph-based feature selection for object-oriented classification in VHR airborne imagery[J]. IEEE Transactions on Geoscience and Remote Sensing,， 2011,， 49（1）： 353-365.

　　[16] SAUL L K， ROWEIS S T. Think globally,， fit locally： unsupervised learning of low dimensional manifolds[J]. Journal of Machine Learning Research,， 2003（4）：119-155.