文獻標識碼： A
DOI：10.16157/j.issn.0258-7998.2015.09.004
中文引用格式： 李彤巖,，王培國,，張婷. 基于ADC模型的通信網絡效能評估方法研究[J].電子技術應用，2015,，41(9)：18-20,，28
英文引用格式： Li Tongyan，Wang Peiguo,，Zhang Ting. Effectiveness evaluation method based on ADC model in communication networks[J].Application of Electronic Technique,，2015，41(9)：18-20,，28
0 引言
網絡的故障情況及可靠性是網絡性能的重要衡量指標，也是效能評估系統主要考核的指標[1],。但是現代通信網絡的特點是傳輸速度快,、網絡規(guī)模大,、網絡復雜性高和異構性，因此使得網絡故障管理成為通信網絡管理中的一個難題,。目前針對網絡性能分析和評估的研究并不多,，且缺乏有效的評估手段。因此,，網絡管理的綜合化,、自動化和智能化成為網絡管理未來的發(fā)展方向。隨著網絡的發(fā)展和日益復雜化,，迫切需要建立與之適應的網絡保障體制和效能評估系統,。
對網絡性能進行評估，傳統的方法有層次分析法[2-3]和神經網絡方法[4]等,。其中,，將層次分析法用到柵格化信息網中效果不好，因為影響網絡性能的指標參數數量多,，指標之間的相互影響不便定量分析,，因此建立層次模型會有很大的難度；采用神經網絡方法又會造成訓練過于復雜,，從而導致評估的效率差,，不利于針對現代通信網絡的特點進行有效的評估。
ADC模型源于美國工業(yè)界武器系統效能咨詢委員會(WSEIAC)于20世紀60年代中期為美國空軍建立的模型,，旨在根據武器系統的有效性(可用度) ,、可信賴性和能力三大要素評價裝備系統。該模型層次清晰, 易于理解和計算, 可以進行變量間關系的分析,，是一種較為優(yōu)秀的效能評估方法, 在諸多領域得到廣泛應用[5-8],，但是應用在通信網絡領域并不多。相比較傳統的評估方法,，基于ADC模型的評估方法更能夠科學地分析影響網絡性能的各個指標,，智能分析結果并評估網絡的可靠性，最后制定出包含網絡運維,、檢查,、服務、安全及設備維修等五類指標體系及考評策略,，并對網元的擴充和調整給出合理建議,，從而為網絡維護和資源優(yōu)化配置提供了合理有效的依據。
本文根據通信網絡的實際特點,，設計了基于ADC模型的網絡效能評估系統,，并且采用了可視化的實現。整個系統結合了專家經驗和客觀指標值來設計，能夠提高評價的科學性和有效性,。
1 基于ADC模型的效能評估系統
1.1 ADC模型
ADC評估模型的解析表達式為:
E=A·D·C(1)
式(1)中,，E為系統效能；A是可用性行向量,，表示系統在任意隨機時刻開始執(zhí)行任務瞬間處于不同狀態(tài)的概率,，表達式為A=(a1，a2,，…,，an)，其中n為狀態(tài)數目,；D為可信賴矩陣,，用于描述處于不同狀態(tài)的概率；C為能力向量,，是系統效能在已知各個狀態(tài)時系統完成任務的能力度量,，是系統性能集中的體現，表達式為C=[c1,，c2,，…，cn]T,，其中矩陣元素ci是裝備系統在狀態(tài)i時的能力。
根據通信網的實際特點,，本文提出了如圖1所示的基于ADC模型的通信網絡效能評估系統,，其中模型中的參數A、D,、C分別表示可用性行向量,、可信賴性矩陣和通信保障能力。
1.2 ADC模型參數定義
1.2.1 可用性行向量A
可用性行向量A是由系統開始處于所有可能狀態(tài)的概率組成, 一般表達式為：A=[a1,，a2],，兩種可能狀態(tài)構成了樣本空間。假設通信系統在開始執(zhí)行任務時狀態(tài)僅劃分為完全正常工作(用數字1表示)和發(fā)生故障(用數字 0表示)兩種狀態(tài),，則系統的可用性向量可表示為A,，式中a1表示系統在開始執(zhí)行任務時處于完全正常工作狀態(tài)的概率(即可用度), a2表示系統在開始執(zhí)行任務時處于發(fā)生部分故障狀態(tài)的概率(即不可用度1)。根據可靠性理論有：
其中,，完全正常的概率,，為完全故障的概率。
1.2.2 可信賴性矩陣D
通信安全設備在執(zhí)行任務中,，按正常工作和發(fā)生故障兩種狀態(tài),，系統可信賴性矩陣為：
式中dij為i狀態(tài)轉移到j狀態(tài)的轉移概率。
1.2.3 能力矩陣C
能力矩陣C表示系統在各個可用狀態(tài)下的能力, 是指在已知系統執(zhí)行任務過程中所處狀態(tài)條件下達到任務目標的能力向量。作為通信保障系統,其能力主要包括信息處理過程的準確性,、安全性及傳輸的完整性等,。通信系統在執(zhí)行任務過程中只有正常故障狀態(tài)三種模式，因此能力矩陣C可表示為：
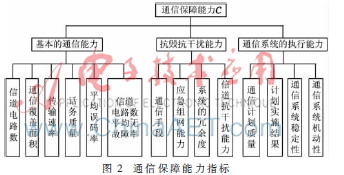
根據某地區(qū)的情況,，給出了如圖2所示的通信保障能力的能力指標確定,。
對通信保障能力采用加權合成綜合評估模型計算能力向量：
1.3 ADC模型中參數的設計
1.3.1 可用性行向量A
網絡運行可分為三種情況：完全正常率、部分故障率,、完全故障率,。a1為正常運行時間，a2為故障運行時間,。根據統計數據分別得到運行時的概率p(a1),、p(a2)，可根據三種狀態(tài)的統計時長分別除以總時長得到：
1.3.2 可信賴矩陣D
dij為i狀態(tài)轉移到j狀態(tài)的轉移概率,，d11為正常情況下的概率,，d12為正常情況變成部分故障的概率，d21為部分故障變成正常的修復率,，d22為部分故障維持不變的概率,。可信賴矩陣D描述為：
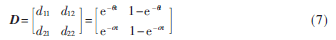
其中,，表示系統的故障率,t為累計運行時間,。
1.3.3 能力矩陣C
為了方便計算，能力矩陣C中大部分取值為0~100%,。
1.4 評估過程
效能評估過程的流程圖如圖3所示,。
效能評估部分需要輸入各個評估項目的打分情況和參數權值，輸出的則是該項目方案當前系統的評估值,。根據評估值可以判斷系統的運行情況,。
2 實驗測試
針對某區(qū)網絡實際情況對評估系統進行了測試，其中效能評估分為輸入參數部分和矩陣計算兩大部分,。效能評估時首先對程序的原始設定進行清空,，然后設置可用性行向量A、能力矩陣C各個選項的權值以及可信賴矩陣D,，根據A,、D、C矩陣計算顯示評估結果,。計算結果保存需要用到MySql數據庫,。
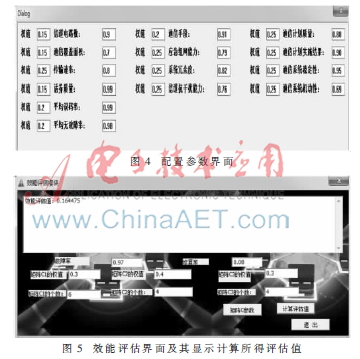
評估過程各個參數的設定需要人工進行評分，范圍為0~100%,，包含了好,、中,、差三種情況的結果對應值。依據某網絡性能的客觀指標值設置各參數情況如圖4所示,。圖5為可視化界面,，描述了根據圖4對矩陣C各參數的配置設定得到的效能評估值。
選取某通信網絡的幾個重要性能指標,，測試在參數取值不同的情況下對通信效能評估值的影響,，測試結果如表1所示。
通過理論分析可知道,，A和D的取值情況會受到網絡故障診斷的影響,，通信保障能力C則綜合反映了幾個性能指標對網絡性能的影響程度。通過實驗測試結果可以得出,，信道抗干擾能力,、平均無故障率和通信系統機動性是影響網絡性能的三個最主要因素，隨著抗干擾能力,、平均無故障率,、通信系統機動性的增強，網絡效能評估值相應提高,。實驗表明通過對各個參數具體的設定,，可以較好地將影響網絡性能的因素反映在效能評估模型中。該方法能夠比較科學有效地分析,、評估通信保障效能,。通過ADC模型得出的評估值，可以用來對網絡資源進行優(yōu)化配置,，并給管理者提供可靠的決策依據,。
3 結束語
本文根據柵格化信息網的特點來構建效能評估模型，解決了性能指標過多而不便于客觀科學地評估網絡保障效能的問題,。對網絡保障效能評估系統采用了可視化的實現，解決了傳統評估系統操作不方便,、不利于應用推廣的問題,。整個系統結合了專家經驗和客觀指標值來設計，提高了評價的科學性,。柵格化信息網保障效能評估系統是提高網絡可靠性,，提高信息網保障效能的必然需求。該平臺能夠對信息網絡管理中產生的大量數據進行挖掘和分析,，為信息網保障效能提供了科學的依據,。
參考文獻
[1] 石磊，潘平俊.網絡戰(zhàn)裝備綜合效能評估框架[J].現代防御技術,，2008,，36(4)：1-5.
[2] HAN W T,QI K W.Evaluation on the armed police force transport safety ensuring effectiveness based on the AHP-FUZZY[J].Applied Mechanics and Materials,2012,198：1646-1651.
[3] DONG S S，HJU Y N.The application effectiveness evalua-tion of the educational equipment based on AHP[J].Advanced Materials Research，2012,，341：384-389.
[4] ZHU F,，LI G，LI Z,，et al.A case study of evaluating trafficsignal control systems using computational experiments[J].Intelligent Transportation Systems,，IEEE Transactions on，2011,，12(4)：1220-1226.
[5] MA L,，WANG H，SONG G,，et al.Analysis of missile weapon system ADC effectiveness model[J].Journal of NavalAeronautical Engineering Institute,，2006(4)：20.
[6] DARBY R R.SEPARATING agency from deeds in immoral neurological Patients：a potential challenge to the ADC model [J].AJOB Neuroscience，2014,，5(4)：25-27.
[7] WANG J,，ZHOU L，BAI H.Arithmetic of dependability matrixes in the ADC effectiveness evaluation model[J].SystemsEngineering and Electronics,，2008(8)：29.
[8] MCCULLOUGH J C,，AGARWAL Y，CCHANDRASHEKAR J,，et al.Evaluating the effectiveness of model-based power characterization[C].USENIX Annual Technical Conf,，2011.