文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.2015.08.029
中文引用格式: 蔡琛,陳運(yùn),萬武南,等. 基于主成分分析的AES算法相關(guān)功耗分析攻擊[J].電子技術(shù)應(yīng)用,2015,41(8):101-105.
英文引用格式: Cai Chen,Chen Yun,Wan Wunan,et al. Correlation power analysis for AES based-on principal component analysis[J].Application of Electronic Technique,2015,41(8):101-105.
0 引言
密碼設(shè)備運(yùn)行算法時(shí)產(chǎn)生時(shí)間[1]、功耗[2]、電磁[3]等邊信息泄露,泄露的邊信息與加密運(yùn)算中的操作或數(shù)據(jù)存在相關(guān)性,利用這些邊信息攻擊密鑰的方法叫邊信道攻擊。功耗分析攻擊(Power Attacks,PA)[4-5]是其中一種邊信道攻擊(Side Channel Attack,SCA)[6-7]方法。攻擊者采集密碼設(shè)備運(yùn)行時(shí)的功耗,通過對(duì)功耗信息進(jìn)行分析來破解密鑰。在信息安全形勢(shì)日漸嚴(yán)峻的今天,邊信道安全越來越被學(xué)術(shù)和工業(yè)界重視。
功耗分析攻擊主要分為簡(jiǎn)單功耗分析攻擊(Simple Power Analysis,SPA)[2]、差分功耗分析攻擊(Differential Power Analysis,DPA)[2]、模板攻擊(Template Attack,TA)[8]和相關(guān)功耗分析攻擊(Correlation Power Analysis,CPA)[9-10]。CPA是上述方法中對(duì)功耗信息利用較好的方法[11-12]。然而,相關(guān)功耗分析攻擊中計(jì)算相關(guān)系數(shù)相當(dāng)耗時(shí),尤其在單條功耗曲線功耗采樣點(diǎn)過多時(shí)尤其明顯,所以采用預(yù)處理技術(shù)在CPA前對(duì)功耗曲線進(jìn)行壓縮十分必要。
黃永遠(yuǎn)等[13]提出頻域輔助分析的濾波方法來濾除相關(guān)性低的部分,該方法使用低通濾波后的功耗曲線所執(zhí)行的攻擊效率最高。《能量分析攻擊》[14]提出了最大值提取、原始整合、絕對(duì)值整合、平方和整合的方法來整合一個(gè)時(shí)鐘周期內(nèi)的點(diǎn),達(dá)到壓縮曲線的目的。
引入主成分分析[15](Principal Component Analysis,PCA)到功耗分析的預(yù)處理階段,提取功耗信息中的主要成分,拋棄次要成分,再進(jìn)行相關(guān)功耗分析攻擊,從而提高攻擊效率。主成分分析在簡(jiǎn)單功耗分析以及模板攻擊中有良好的效果,尤其是在模板攻擊中。
與模板攻擊和簡(jiǎn)單功耗分析的閾值判別法不同,相關(guān)功耗分析攻擊通過計(jì)算猜測(cè)值與實(shí)測(cè)值的相關(guān)性來攻擊密鑰。而相關(guān)性的計(jì)算對(duì)具體的數(shù)值、度量單位、密碼算法的種類并不敏感,因此其應(yīng)用范圍以及攻擊效果比模板攻擊和簡(jiǎn)單功耗分析優(yōu)秀。將主成分分析引入相關(guān)功耗分析攻擊具有更廣泛的實(shí)用意義,并以AES算法為例進(jìn)行了驗(yàn)證。
1 經(jīng)典AES算法的相關(guān)功耗分析攻擊
高級(jí)加密標(biāo)準(zhǔn)(Advanced Encryption Standard,AES)是最有代表性的分組密碼加密算法,在全球廣泛應(yīng)用并被多方分析。因此本文以AES為研究對(duì)象。
相關(guān)功耗分析攻擊利用是實(shí)際測(cè)量功耗與其對(duì)應(yīng)的操作數(shù)的漢明重量之間的相關(guān)性來破解密鑰。
詳細(xì)步驟如下:
(1)采集加密時(shí)的功耗信息得到實(shí)測(cè)功耗矩陣X。用示波器采集加密設(shè)備加密時(shí)的n(n∈N+)條功耗曲線,每條曲線有p(p∈N+)個(gè)功耗點(diǎn)。將原始數(shù)據(jù)寫成矩陣形式,矩陣X每一行為一條功耗曲線,每列為按時(shí)間對(duì)齊的p個(gè)功耗采樣點(diǎn)的值:

(2)選擇算法中間值。根據(jù)文獻(xiàn)[14]的描述,中間值應(yīng)為明文與密鑰或密文與密鑰的函數(shù)值。現(xiàn)選取AES算法第一輪輪密鑰加操作后S盒的輸出值為算法中間值。如圖1所示,8 bit明文和8 bit密鑰在執(zhí)行輪密鑰加異或操作之后,得到8 bit的結(jié)果,作為S盒的輸入,查詢S盒,得到S盒的輸出。

(3)計(jì)算假設(shè)中間值。
對(duì)可能的密鑰假設(shè)k=(k1,k2,…,k256),輸入明文P=(P1,P2,…,Pn),n為明文數(shù)量,計(jì)算假設(shè)中間值矩陣V,大小為n×256。計(jì)算公式:
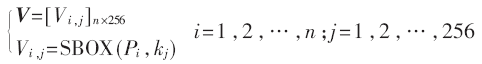
其中,符號(hào)SBOX(Pi,kj)為AES算法S盒替代操作函數(shù)。
(4)將假設(shè)中間值映射為假設(shè)功耗。
漢明重量是字符串中非零的元素個(gè)數(shù)。以漢明重量模型為功耗模型,給出相關(guān)功耗分析攻擊法映射的步驟,其中V為假設(shè)中間值矩陣,符號(hào)HW()表示計(jì)算輸入字符串漢明重量的功能函數(shù)。計(jì)算假設(shè)功耗矩陣H公式如下:

其每一行對(duì)應(yīng)一個(gè)假設(shè)密鑰。首先找出每一行最大的相關(guān)系數(shù)值,得到256個(gè)相關(guān)系數(shù)值。接著對(duì)這256個(gè)相關(guān)系數(shù)值從大到小排序,最大的相關(guān)系數(shù)值對(duì)應(yīng)的密鑰值(即矩陣行號(hào))為最佳密鑰候選值,次大的相關(guān)系數(shù)值對(duì)應(yīng)的密鑰值(即矩陣行號(hào))為次佳候選值,以此類推。最終得到了一個(gè)字節(jié)密鑰對(duì)應(yīng)的256個(gè)候選密鑰值。選取最佳候選密鑰值為該字節(jié)密鑰的猜測(cè)值。對(duì)其他算法密鑰字節(jié)值都采用類似的方法進(jìn)行猜測(cè)。
2 基于主成分分析的AES相關(guān)功耗分析攻擊
與經(jīng)典相關(guān)功耗分析攻擊不同的是:經(jīng)典相關(guān)功耗分析攻擊直接使用實(shí)測(cè)功耗X進(jìn)行攻擊,而本方法先對(duì)實(shí)測(cè)功耗X進(jìn)行主成分分析預(yù)處理得到矩陣Y,再用矩陣Y進(jìn)行攻擊。
2.1 主成分分析
信號(hào)處理中,主成分分析被用來提取一個(gè)混合信號(hào)中的主成分[16],拋棄次要成分,將復(fù)雜數(shù)據(jù)降維。它的優(yōu)點(diǎn)是簡(jiǎn)單,無參數(shù)限制,可以方便地應(yīng)用于各種場(chǎng)合,因此應(yīng)用極其廣泛。
將原來p個(gè)指標(biāo)記為X1,X2,…,Xp。尋求這p個(gè)變量的線性組合Y1,Y2,…,Ym,(m≤p):Ym即為主成分分析后的主成分,用這m個(gè)主成分來表示原始數(shù)據(jù)中的大部分信息,用累積貢獻(xiàn)率來衡量這m主成分對(duì)原始數(shù)據(jù)信息的表示程度。其滿足如下性質(zhì):
(1)主成分的方差Var(Yi)(i=1,2,…,p)依次遞減,重要性依次遞減,即:
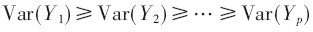
(2)主成分之間互不相關(guān),即無重疊的信息。協(xié)方差Cov有如下性質(zhì):
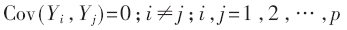
性質(zhì)(2)保證每個(gè)主成分都是不相關(guān)的,即保證每個(gè)主成分都不包含其他主成分的信息,從而保證最大化降維。性質(zhì)(1)則保證能表示更多信息的成分在主成分編號(hào)中較小。
2.1.1 主成分分析功耗曲線預(yù)處理計(jì)算步驟
將第1小節(jié)采集到n條功耗曲線,每條曲線有p個(gè)功耗點(diǎn)的功耗矩陣X進(jìn)行預(yù)處理。步驟如下:

T即為計(jì)算主成分的轉(zhuǎn)換矩陣。
一般取累計(jì)貢獻(xiàn)率達(dá)85%~95%的特征值λ1,λ2,…,λm所對(duì)應(yīng)的第1、第2、…、第m(m≤p)個(gè)主成分。
2.1.2 主成分的貢獻(xiàn)率
主成分分析的目的是減少變量的個(gè)數(shù),所以一般不會(huì)使用所有p個(gè)主成分的,忽略一些帶有較小方差的主成分將不會(huì)給總方差帶來太大的影響。
這里稱 為第k(k>0)個(gè)主成分Yk的貢獻(xiàn)率。第一主成分的貢獻(xiàn)率最大,這表明Y1綜合原始變量X1,X2,…,Xp的能力最強(qiáng),而Y2,Y3,…,Yp的綜合能力依次遞減。若只取m個(gè)主成分,則稱
為第k(k>0)個(gè)主成分Yk的貢獻(xiàn)率。第一主成分的貢獻(xiàn)率最大,這表明Y1綜合原始變量X1,X2,…,Xp的能力最強(qiáng),而Y2,Y3,…,Yp的綜合能力依次遞減。若只取m個(gè)主成分,則稱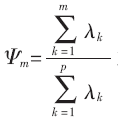 為主成分Y1,…,Ym的累計(jì)貢獻(xiàn)率,累計(jì)貢獻(xiàn)率表明Y1,…,Ym綜合X1,X2,…,Xp的能力。通常取m,使得累計(jì)貢獻(xiàn)率達(dá)到一個(gè)較高的百分?jǐn)?shù),如85%以上。
為主成分Y1,…,Ym的累計(jì)貢獻(xiàn)率,累計(jì)貢獻(xiàn)率表明Y1,…,Ym綜合X1,X2,…,Xp的能力。通常取m,使得累計(jì)貢獻(xiàn)率達(dá)到一個(gè)較高的百分?jǐn)?shù),如85%以上。
2.2 實(shí)驗(yàn)
2.2.1 實(shí)驗(yàn)環(huán)境
加密設(shè)備用Atmel ATME0A16A為硬件仿真平臺(tái),采用Tektronix DPO4032示波器采集硬件仿真平臺(tái)加密隨機(jī)明文時(shí)的功耗。選取AES算法第一輪S盒輸出做中間值,用漢明重量做功耗模型進(jìn)行相關(guān)功耗分析攻擊。
2.2.2 基于主成分分析的功耗曲線預(yù)處理
使用示波器以100 MHz采樣頻率采集5組樣本數(shù)據(jù),每組樣本有10 000條功耗曲線,每條曲線6 700個(gè)功耗采樣點(diǎn)。在上文硬件平臺(tái)下的相關(guān)功耗攻擊出全部16 B密鑰需要100條左右曲線,因此樣本量選擇10 000能保證實(shí)驗(yàn)結(jié)果的穩(wěn)定可靠。對(duì)5組樣本分別進(jìn)行主成分分析預(yù)處理,為下一步三種方案對(duì)比實(shí)驗(yàn)方案做準(zhǔn)備。
按照2.1.1節(jié)主成分分析功耗曲線預(yù)處理計(jì)算步驟進(jìn)行預(yù)處理:
(1)n=10 000條功耗曲線,每條曲線有p=6 700個(gè)功耗采集點(diǎn)的值,原始數(shù)據(jù)寫成矩陣形式,得到矩陣X:

每一行是一條曲線樣本,每一列是對(duì)應(yīng)時(shí)刻采樣點(diǎn)的功耗值。對(duì)矩陣X進(jìn)行標(biāo)準(zhǔn)化。
(2)建立變量的協(xié)方差矩陣Cov,求協(xié)方差矩陣Cov的特征根λ1,λ2,…,λ6 700,及相應(yīng)的單位特征向量:T1,T2,…,T6 700。求得轉(zhuǎn)換矩陣T=[T1,T2,…,T6 700]。貢獻(xiàn)率向量L=[λ1,λ2,…,λ6 700]。
(3)矩陣Y=T′X,得到矩陣Y:

矩陣Y的每一行是主成分分析處理后的一條曲線樣本,每列都表示一個(gè)主成分,第一列為一號(hào)主成分,第二列為二號(hào)主成分,依次類推。
向量L=[λ1,λ2,…,λ6 700],λp為第p號(hào)主成分的貢獻(xiàn)率,用2.1.2節(jié)的方法計(jì)算累積貢獻(xiàn)率曲線,把Y矩陣的每一行回寫為功耗曲線的形式,預(yù)處理完成。
預(yù)處理前的曲線示例如圖2所示, 主成分分析后的曲線示例如圖3所示。


通過圖3發(fā)現(xiàn)幅值大的功耗點(diǎn)都是前若干主成分,越靠后的主成分值越小并有向零趨近的趨勢(shì),結(jié)合圖4累積貢獻(xiàn)率可以發(fā)現(xiàn)前若干號(hào)主成分貢獻(xiàn)率明顯高于后面的主成分,該結(jié)果符合進(jìn)行PCA后的理論預(yù)期。
用2.1.2節(jié)的方法計(jì)算累積貢獻(xiàn)率如圖4所示。
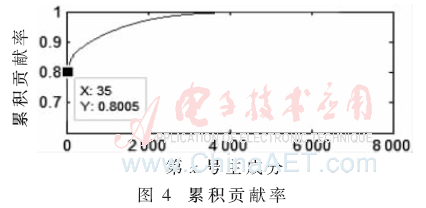
實(shí)驗(yàn)結(jié)果表明,累積貢獻(xiàn)率迅速上升到0.8即80%以上,前35號(hào)主成分就能表示全部6 700個(gè)功耗點(diǎn)80.05%的信息,前141號(hào)主成分累積貢獻(xiàn)率為85.01%。多次實(shí)驗(yàn)顯示,相關(guān)性高的主成分集中在前若干主成分中,35~141號(hào)主成分只包含5%的信息。原始采樣點(diǎn)為6 700,為了實(shí)驗(yàn)對(duì)比的方便,選擇前67號(hào)主成分對(duì)比實(shí)驗(yàn),此時(shí)單條曲線使用的點(diǎn)數(shù)量為原始點(diǎn)數(shù)的1%。
2.2.3 對(duì)比實(shí)驗(yàn)
為了驗(yàn)證主成分分析預(yù)處理的效果,設(shè)計(jì)3種實(shí)驗(yàn)方案進(jìn)行對(duì)比。
實(shí)驗(yàn)方案1:對(duì)原始功耗曲線進(jìn)行相關(guān)功耗分析攻擊,此時(shí)使用原始功耗矩陣X作為分析的功耗數(shù)據(jù)。
實(shí)驗(yàn)方案2:為了找出主成分分析預(yù)處理對(duì)攻擊成功率的影響,取預(yù)處理后的全部6 700號(hào)主成分進(jìn)行相關(guān)功耗分析攻擊,即此時(shí)使用矩陣Y作為分析的功耗數(shù)據(jù)。
實(shí)驗(yàn)方案3:為了驗(yàn)證單條曲線使用的點(diǎn)數(shù)量為原始點(diǎn)數(shù)的1%時(shí)的攻擊效果,預(yù)處理后曲線取前67號(hào)主成分進(jìn)行相關(guān)功耗分析攻擊,即此時(shí)使用矩陣Y的前67列作為分析的功耗數(shù)據(jù)。
實(shí)驗(yàn)結(jié)果如表1、表2和表3所示。
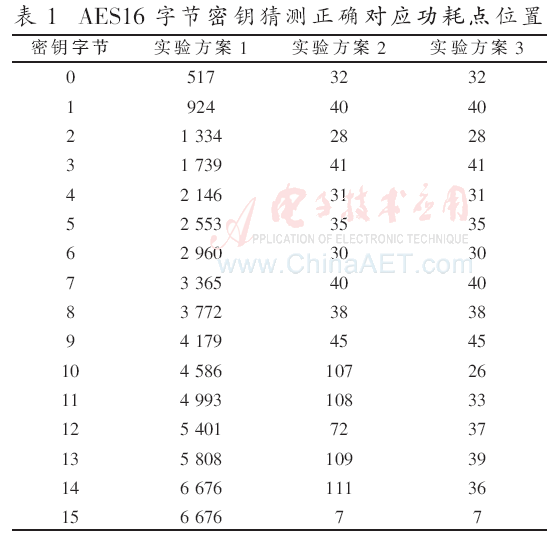
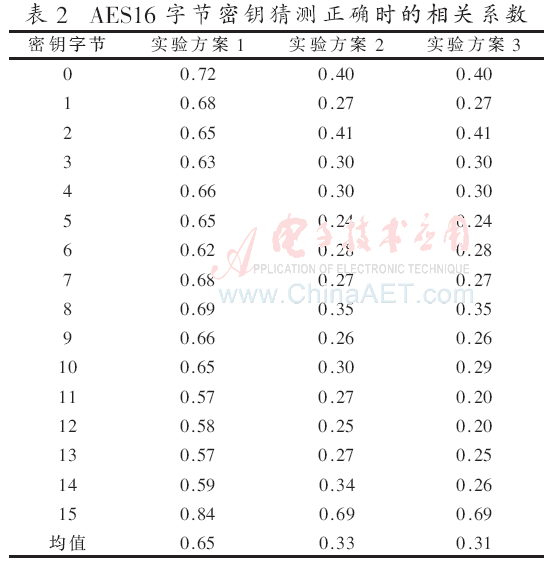

表1中的功耗點(diǎn)位置表示功耗曲線中與當(dāng)前字節(jié)密鑰相關(guān)系數(shù)最高的點(diǎn),即猜測(cè)出正確密鑰的點(diǎn)。
實(shí)驗(yàn)方案1和實(shí)驗(yàn)方案2對(duì)比,區(qū)別是實(shí)驗(yàn)2比實(shí)驗(yàn)1多做了主成分分析預(yù)處理。結(jié)果說明主成分分析后若是依然采用全部6 700個(gè)點(diǎn)進(jìn)行相關(guān)功耗分析攻擊,雖然都能攻擊出全部16 B密鑰,但是所需曲線上升至565,相關(guān)系數(shù)下降了0.32,相關(guān)性降低了。但是,中間值相關(guān)性最高的點(diǎn)全部在前111號(hào)主成分中,說明主成分分析有效地將信息集中到了前111號(hào)主成分。
實(shí)驗(yàn)方案3和實(shí)驗(yàn)方案2的區(qū)別是:實(shí)驗(yàn)方案2使用了全部的6 700號(hào)主成分,而實(shí)驗(yàn)方案3只使用了前67號(hào)主成分就能恢復(fù)出全部的16 B密鑰,且只用了445條曲線。再次說明主成分分析有效地把多數(shù)信息集中到了前若干主成分,主成分分析的降維效果顯著。
在2.1.1的第3步中得出第4步計(jì)算主成分時(shí)所用的轉(zhuǎn)換矩陣T,在保證采樣環(huán)境不變的情況下再次進(jìn)行主成分分析預(yù)處理時(shí),轉(zhuǎn)換矩陣T可以作為先驗(yàn)知識(shí)來使用,即再次進(jìn)行同樣環(huán)境的功耗數(shù)據(jù)預(yù)處理時(shí)只需進(jìn)行第4步。而該步驟是一個(gè)簡(jiǎn)單的線性運(yùn)算,其復(fù)雜度低于計(jì)算相關(guān)系數(shù)。為了比較實(shí)驗(yàn)方案3和實(shí)驗(yàn)方案1的計(jì)算量,假設(shè)該步驟和相關(guān)系數(shù)計(jì)算花費(fèi)一樣的時(shí)間,由于先驗(yàn)知識(shí)可以預(yù)處理1 000條,取前67個(gè)主成分即可穩(wěn)定破解密鑰,此時(shí)處理的點(diǎn)數(shù)為:
S0=1 000×67=67 000
相關(guān)功耗分析攻擊會(huì)計(jì)算每個(gè)功耗點(diǎn)和中間值的相關(guān)性。設(shè)N為CPA成功時(shí)所用的功耗曲線條數(shù),P為每條曲線的實(shí)際使用的點(diǎn)數(shù),攻擊程序分析的功耗點(diǎn)數(shù)為:S=N×P。
實(shí)驗(yàn)方案1分析的功耗點(diǎn)數(shù)為:
S1=60×6 700=402 000
實(shí)驗(yàn)方案3分析的功耗點(diǎn)數(shù)為:
S3=445×67=29 815
對(duì)比實(shí)驗(yàn)方案3和實(shí)驗(yàn)方案1花費(fèi)的時(shí)間:
S1/(S3+S0)=4.15
實(shí)驗(yàn)方案1比實(shí)驗(yàn)方案3多計(jì)算了4.15倍的功耗點(diǎn)。因此主成分分析預(yù)處理在AES的相關(guān)功耗分析攻擊中是能有效的減少攻擊時(shí)間的。
3 結(jié)論
針對(duì)相關(guān)功耗分析攻擊中,當(dāng)功耗曲線的功耗采樣點(diǎn)較多時(shí)攻擊速度緩慢的問題,引入了基于主成分分析的預(yù)處理方法,提取功耗信息中的主成分,減少相關(guān)功耗分析攻擊中分析量。引入主成分分析的相關(guān)功耗分析攻擊與經(jīng)典相關(guān)功耗分析攻擊的對(duì)比實(shí)驗(yàn)結(jié)果表明,該方法可以提高攻擊效率。
參考文獻(xiàn)
[1] KOCHER P C.Timing attacks on implementations of diffie-hellman,RSA,DSS,and other systems[A].CRYPTO 1996[C].Berlin:Springer,1996:104-113.
[2] KOCHER P C,JAFFE J,JUN B.Differential power analysis[A].CRYPTO 1999[C].Berlin:Springer,1999:388-397.
[3] QUISQUATER J,SAMYDE D.Electromagnetic analysis(EMA):measures and countermeasures for smart cards[A].E-Smart 2001[C].Berlin:Springer,2001:200-210.
[4] Mayer Sommer R.Smartly analyzing the simplicity and the power of simple power analysis on smartcards[C].Cryptographic Hardware and Embedded Systems-CHES 2000,Springer Berlin Heidelberg,2000:78-92.
[5] NOVAK R.SPA-based adaptive chosen-ciphertext attack on RSA implementation[C].Public Key Cryptography,Springer Berlin Heidelberg,2002:252-262.
[6] LEMKE K,PAAR C,WOLF M.Embedded security in cars[M].New York:Springer,2006.
[7] MESSERGES T S.Securing the AES finalists against power analysis attacks[C].Fast Software Encryption.Springer Berlin Heidelberg,2001:150-164.
[8] CHARI S,RAO J R,ROHATGI P.Template attacks[A].CHES 2002[C].Berlin:Springer,2002:13-28.
[9] PAN W,MARNANE W P.A correlation power analysis attack against tare pairing on FPGA[M].New York:Springer,2011:340-349.
[10] 嚴(yán)迎建,樊海鋒,徐金甫,等.針對(duì)DES密碼芯片的CPA攻擊仿真[J].電子技術(shù)應(yīng)用,2009(7).
[11] KOEUNE F,STANDAERT F X.A tutorial on physical security and side-channel attacks[M].New York:SpringerBerlin Heidelberg,2005:78-108.
[12] SEHIMMEL O,DUPLYS P,BOEH1 E,et a1.Correlation power analysis in frequency domain[J].COSADE,2010.
[13] 黃永遠(yuǎn),陳運(yùn),陳俊,等.運(yùn)用頻域輔助分析的AES算法相關(guān)功耗攻擊[J].四川大學(xué)學(xué)報(bào)(自然科學(xué)版),2014,51(3).
[14] Stefan Mangard,Elisabeth Oswald,Thomas Popp.能量分析攻擊[M].北京:科學(xué)出版社,2010.
[15] 魏艷華,王丙參,田玉柱.主成分分析與因子分析的比較研究[J].天水師范學(xué)院學(xué)報(bào),2009(2).
[16] JOLLIFFE I T.Principal component analysis[A].ACM Computing Surveys[C].New York:Springer Verlag,1986.
[17] 張立軍,袁能文.線性綜合評(píng)價(jià)模型中指標(biāo)標(biāo)準(zhǔn)化方法的比較與選擇[J].統(tǒng)計(jì)與信息論壇,2010(8).

