0 引言

　　橢圓曲線密碼(Elliptic Curve Cryptography，ECC)[1]的算法安全性是建立在解橢圓曲線離散對(duì)數(shù)數(shù)學(xué)難題之上的,，是目前公開密鑰密碼中單位比特長度安全性最高的密碼算法[2],。但是當(dāng)密碼算法在硬件實(shí)現(xiàn)時(shí)，其安全性不僅依賴算法和協(xié)議的安全性,，還要依賴實(shí)現(xiàn)的安全性,。能量分析(Power Analysis，PA)[3]攻擊通過分析密碼設(shè)備工作時(shí)的能量消耗來獲取密碼算法的秘密信息,，避開了求解數(shù)學(xué)難題,，對(duì)密碼系統(tǒng)的安全造成了很大威脅。能量攻擊主要分為簡單能量(Simple Power Analysis,，SPA)[4]攻擊和差分能量(Differential Power Analysis,，DPA)[5]攻擊。其中DPA攻擊是利用密碼設(shè)備能量消耗對(duì)數(shù)據(jù)的依賴性,，利用統(tǒng)計(jì)分析手段分析固定時(shí)刻設(shè)備的能量消耗,，進(jìn)而獲取運(yùn)算過程中的秘密信息，成為最具威脅的能量攻擊手段,，因此有必要對(duì)密碼設(shè)備進(jìn)行抗DPA攻擊設(shè)計(jì),。

　　時(shí)間是影響DPA攻擊的重要因素，DPA攻擊之所以能夠成功,，是因?yàn)槊艽a設(shè)備每次執(zhí)行的相應(yīng)運(yùn)算操作都會(huì)出現(xiàn)在固定的時(shí)間點(diǎn)上,，因此可以從時(shí)間角度對(duì)密碼設(shè)備進(jìn)行抗DPA攻擊設(shè)計(jì)。時(shí)間隨機(jī)化通過在密碼設(shè)備運(yùn)行過程中插入隨機(jī)時(shí)間延遲,，擾亂功耗與操作和數(shù)據(jù)的關(guān)系,，使統(tǒng)計(jì)分析手段失效，進(jìn)而達(dá)到抗DPA攻擊的目的,。目前常用的時(shí)間隨機(jī)化技術(shù)主要有多時(shí)鐘技術(shù)[6],、門控時(shí)鐘延遲技術(shù)[7]、冗余指令延遲等,，其中多時(shí)鐘技術(shù)要求系統(tǒng)中有多個(gè)時(shí)鐘源,，并且會(huì)增加系統(tǒng)的控制復(fù)雜度,；門控時(shí)鐘延遲技術(shù)產(chǎn)生的隨機(jī)延遲部分表現(xiàn)在能量跡上為一段直線，很容易被區(qū)分剔除,；由于ECC處理器的運(yùn)算指令為多周期指令,，且不同指令的周期不同，導(dǎo)致時(shí)間延遲的基本粒度較大,，不利于控制,。

　　針對(duì)上述問題，本文在分析了時(shí)間隨機(jī)化抗能量攻擊原理的基礎(chǔ)上,，結(jié)合ECC處理器的處理特點(diǎn),，有針對(duì)性的設(shè)計(jì)了基于軟中斷的可配置時(shí)間隨機(jī)化抗DPA攻擊電路，并對(duì)其進(jìn)行仿真分析,，結(jié)果表明本文設(shè)計(jì)的時(shí)間隨機(jī)化電路能夠達(dá)到抗能量攻擊的目的,。

1 時(shí)間隨機(jī)化抗DPA攻擊原理分析

　　設(shè)密碼設(shè)備正常工作時(shí)的功耗采樣信號(hào)為T[i][j]，其中i為采樣樣本,，j為采樣點(diǎn),，由DPA攻擊的原理可知，需要樣本空間N足夠大,，即需要采集N組功耗數(shù)據(jù),。定義一組區(qū)分函數(shù)D[i][j]→(0，1),，將采集到的功耗數(shù)據(jù)分為兩組T0={T[i][j]|D[i][j]=0},，T1={T[i][j]|D[i][j]=1}。當(dāng)N足夠大時(shí),，集合T0,、T1中的樣本數(shù)量近似相等，設(shè)為m,，則采樣點(diǎn)j處的差分功耗為：

　　差分功耗的數(shù)學(xué)期望為：

　　E(TD[j])=E(T[i][j]|D[i][j]=0)-E(T[i][j]|D[i][j]=1)

　　設(shè)在運(yùn)算過程中插入隨機(jī)延遲t后的功耗采樣信號(hào)為T*[i][j],，攻擊者不知道插入隨機(jī)時(shí)間延遲的情況下，仍然使用攻擊正常工作設(shè)備時(shí)構(gòu)造的區(qū)分函數(shù)D[i][j]來對(duì)數(shù)據(jù)進(jìn)行分組處理,，得到T={T*[i][j]|D[i][j]=0},，T={T*[i][j]|D[i][j]=1}，則采樣點(diǎn)j處的差分功耗為：

　　此時(shí),，差分功耗的數(shù)學(xué)期望為：

　　E(T[j])=E(T*[i][j]|D[i][j]=0)-E(T*[i][j]|D[i][j]=1)

　　設(shè)隨機(jī)延遲t有w種可能值,，延遲t等于k的概率為pk，則插入時(shí)間延遲后的采樣信號(hào)可表示為：

　　T*[i][j]=T[i][j-k]

　　那么,，插入隨機(jī)時(shí)間延遲后的差分功耗的數(shù)學(xué)期望可以表示為：

　　由DPA攻擊的原理知,，正常情況下，當(dāng)密鑰猜測(cè)正確時(shí)，差分功耗曲線會(huì)在時(shí)間點(diǎn)n處出現(xiàn)尖峰,，設(shè)尖峰的幅值為A,，其他點(diǎn)處與區(qū)分函數(shù)D不相關(guān)，所以差分功耗值約等于0,，即：

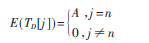
　　當(dāng)插入隨機(jī)延遲?駐t后,，密鑰猜測(cè)正確時(shí)的功耗曲線尖峰會(huì)分布在w+1個(gè)位置處，每個(gè)位置的差分功耗值為pk A,，即：

　　以時(shí)間延遲t服從均勻分布為例,，即pk=1/(w+1)，則加入隨機(jī)延遲后的差分功耗尖峰會(huì)均勻分布在w+1個(gè)位置上,，且每個(gè)尖峰的幅值為A/(w+1),。

2 ECC處理器的時(shí)間隨機(jī)化設(shè)計(jì)

　　為了更好地在ECC處理器中實(shí)現(xiàn)時(shí)間隨機(jī)化,，達(dá)到抗能量攻擊的目的,，必須分析時(shí)間隨機(jī)化的設(shè)計(jì)要求和ECC處理器的特征，提出合適的設(shè)計(jì)方案,。

　　2.1 ECC處理器時(shí)間隨機(jī)化設(shè)計(jì)方案

　　結(jié)合上一節(jié)的分析,，為了兼顧安全和效率兩個(gè)方面，時(shí)間隨機(jī)化設(shè)計(jì)需要滿足以下要求：

　　(1)安全性好,。功耗曲線上時(shí)間延遲部分不易被區(qū)分剔除,，即要求時(shí)間延遲部分的功耗特性和算法中的正常運(yùn)算操作的功耗特性相似，并且每次的延時(shí)時(shí)間隨機(jī)產(chǎn)生,。

　　(2)靈活性高,。在正常計(jì)算過程中插入的延遲時(shí)間越長，抗能量攻擊效果越好,，但是對(duì)算法的效率影響也越大,。因此，處理器的時(shí)間隨機(jī)化設(shè)計(jì)需要滿足不同的安全需求,，能夠根據(jù)具體情況選擇一個(gè)安全與效率的平衡點(diǎn),，設(shè)置隨機(jī)時(shí)間延遲的范圍。

　　(3)方便使用,。ECC處理器上的時(shí)間隨機(jī)化設(shè)計(jì),，必須方便用戶使用，用戶可以根據(jù)需要在任意時(shí)刻執(zhí)行時(shí)間隨機(jī)化程序,。

　　綜合上述安全性,、靈活性與易用性要求，本文借鑒軟中斷[8]的思想,，對(duì)密碼處理器進(jìn)行時(shí)間隨機(jī)化設(shè)計(jì),。在ECC處理器指令RAM中，存入一段不影響密碼算法正常運(yùn)算的冗余指令，利用中斷指令來執(zhí)行中斷程序,，隨機(jī)地調(diào)用冗余指令,，當(dāng)中斷結(jié)束后，正常程序的執(zhí)行時(shí)間發(fā)生偏移,，達(dá)到時(shí)間隨機(jī)化的目的,。由于時(shí)間隨機(jī)化處理過程中執(zhí)行的是冗余指令，所以其功耗特征與正常運(yùn)算的功耗特征相似,，單條能量跡中不易被區(qū)分,。

　　2.2 基于軟中斷的時(shí)間隨機(jī)化設(shè)計(jì)

　　時(shí)間隨機(jī)化設(shè)計(jì)的一個(gè)關(guān)鍵因素是延遲時(shí)間的隨機(jī)可控，既關(guān)系到抗能量攻擊的效果,，又關(guān)系到對(duì)密碼運(yùn)算的性能影響,。為了設(shè)計(jì)靈活的控制單元，首先分析橢圓曲線密碼處理器的特征：

　　(1)主要運(yùn)算模塊較少,，橢圓曲線各層次的運(yùn)算最終都是基于有限域?qū)拥倪\(yùn)算實(shí)現(xiàn)的,，域運(yùn)算種類比較單一，主要包括為模乘,、模逆,、模加、模減等運(yùn)算,；

　　(2)運(yùn)算指令周期較長,，且同一運(yùn)算指令處理不同長度數(shù)據(jù)時(shí)所用周期不同。表1給出了不同長度曲線對(duì)應(yīng)的基本運(yùn)算單元的時(shí)鐘周期數(shù),。

　　橢圓曲線密碼處理器的這些特征為時(shí)間隨機(jī)化控制帶來難度,，不適合以指令條數(shù)為基本單位進(jìn)行時(shí)間隨機(jī)化控制。一方面,，運(yùn)算指令周期較長,，以指令條數(shù)為粒度進(jìn)行控制會(huì)對(duì)整個(gè)算法的性能影響較大；另一方面,，不同的運(yùn)算指令的周期不同,，且處理不同長度曲線時(shí)，同一運(yùn)算指令需要的時(shí)鐘周期不一致,，這樣無法精確地控制插入的延時(shí)時(shí)間,。考慮到用于實(shí)現(xiàn)隨機(jī)化的冗余指令對(duì)于密碼運(yùn)算沒有實(shí)際的意義,，為了靈活控制隨機(jī)化的程度,，設(shè)計(jì)了以時(shí)鐘周期為基本粒度的隨機(jī)延遲控制單元，如圖1所示,。在執(zhí)行中斷程序時(shí),，生成一個(gè)隨機(jī)數(shù)作為延時(shí)控制計(jì)數(shù)器的計(jì)數(shù)周期,，當(dāng)計(jì)數(shù)器計(jì)數(shù)結(jié)束后，產(chǎn)生一個(gè)進(jìn)位信號(hào)CO,。利用CO信號(hào)控制中斷的返回,，一方面參與生成運(yùn)算模塊的結(jié)束信號(hào)Valid，結(jié)束正在執(zhí)行的冗余運(yùn)算,；另一方面用于生成堆棧寄存器的使能信號(hào)PP_EN和程序計(jì)數(shù)器PC的地址選擇信號(hào)SEL,，控制返回?cái)帱c(diǎn)執(zhí)行正常程序。隨機(jī)數(shù)的值就是執(zhí)行中斷的時(shí)間,，即時(shí)間隨機(jī)化的延遲時(shí)間,。

　　采用軟中斷的時(shí)間隨機(jī)化設(shè)計(jì)，能夠保證中斷時(shí)間延遲部分的功耗特性與正常運(yùn)算的功耗特性一致,，在單條能量跡上無法將其區(qū)分出來,。但是DPA攻擊是通過分析大量能量跡來實(shí)施的，當(dāng)隨機(jī)化的首地址相同時(shí),，通過對(duì)比多條能量跡,，仍然能夠?qū)⒀舆t時(shí)間短的隨機(jī)化部分區(qū)分出來，如圖2所示,。

　　為了解決這個(gè)問題,，將冗余指令RAM的首地址加上可控的隨機(jī)偏移地址作為中斷的跳轉(zhuǎn)地址,，如圖3所示,，這樣執(zhí)行中斷的部分就很難在能量跡中被區(qū)分剔除。

　　上述的延遲時(shí)間隨機(jī)化設(shè)計(jì)解決了中斷時(shí)間靈活控制的問題,，跳轉(zhuǎn)地址隨機(jī)化設(shè)計(jì)解決了隨機(jī)化功耗與正常運(yùn)算功耗一致性的問題,。本文設(shè)計(jì)了級(jí)數(shù)可變的偽隨機(jī)數(shù)發(fā)生器，通過實(shí)際需求配置其級(jí)數(shù)來控制隨機(jī)延遲和隨機(jī)偏移地址的范圍,。在此基礎(chǔ)上設(shè)計(jì)了帶軟中斷的橢圓曲線密碼處理器控制結(jié)構(gòu),，并設(shè)計(jì)了軟中斷指令，支持時(shí)間隨機(jī)化抗能量攻擊功能,，如圖4所示,。

3 時(shí)間隨機(jī)化抗能量攻擊能力驗(yàn)證

　　由于抗DPA攻擊的時(shí)間隨機(jī)化設(shè)計(jì)要求每次運(yùn)算都要發(fā)生隨機(jī)時(shí)間延遲，并且時(shí)間延時(shí)部分對(duì)應(yīng)的功耗不能在單條能量跡上被區(qū)分,，因此從三方面對(duì)設(shè)計(jì)進(jìn)行驗(yàn)證：

　　(1)仿真驗(yàn)證運(yùn)算操作的執(zhí)行時(shí)間是否發(fā)生隨機(jī)延遲,；

　　(2)采集處理器執(zhí)行密碼運(yùn)算的功耗曲線，觀察時(shí)間隨機(jī)化部分的功耗特性與正常運(yùn)算時(shí)的功耗特性是否一致,；

　　(3)進(jìn)行DPA攻擊仿真實(shí)驗(yàn),，驗(yàn)證其抗DPA攻擊效果。

　　3.1 隨機(jī)延遲仿真驗(yàn)證

　　以Montgomery點(diǎn)乘算法[9]為例,，在處理器執(zhí)行算法的過程中通過指令開啟中斷程序,，任意兩次相同輸入的仿真中間結(jié)果如圖5所示,。

　　由圖5可以看出，執(zhí)行中斷程序時(shí),，程序計(jì)數(shù)器PC(Current_PC)的值轉(zhuǎn)向冗余程序地址,，每次跳轉(zhuǎn)地址不同，達(dá)到了跳轉(zhuǎn)地址隨機(jī)的設(shè)計(jì)要求,，每次中斷返回時(shí)間不同,，達(dá)到了時(shí)間隨機(jī)化的設(shè)計(jì)要求。

　　3.2 單條能量跡功耗特性一致性驗(yàn)證

　　采集處理器在執(zhí)行加入軟中斷的算法時(shí)的功耗信息,，如圖6所示,。

　　可以看出冗余運(yùn)算部分與正常運(yùn)算程序的功耗特性一致，不容易被區(qū)分剔除,，滿足了時(shí)間隨機(jī)化部分不可區(qū)分的設(shè)計(jì)要求,。

　　3.3 DPA攻擊仿真驗(yàn)證

　　為了驗(yàn)證基于軟中斷的時(shí)間隨機(jī)化設(shè)計(jì)的抗能量攻擊能力，以Montgomery點(diǎn)乘算法為例,，在執(zhí)行時(shí)啟動(dòng)軟中斷程序,，分別配置隨機(jī)延遲范圍為0~32個(gè)時(shí)鐘周期和0~64個(gè)時(shí)鐘周期，對(duì)其分別進(jìn)行DPA攻擊實(shí)驗(yàn),，并與正常運(yùn)算的DPA攻擊實(shí)驗(yàn)對(duì)比,，結(jié)果如圖7所示。

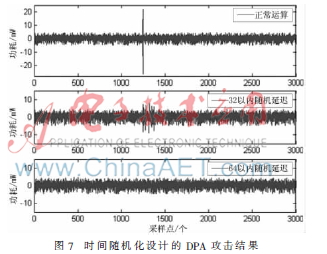
　　由圖7可知,，正常運(yùn)算的差分功耗曲線上攻擊點(diǎn)位置出現(xiàn)了明顯的功耗尖峰,，當(dāng)加入32以內(nèi)的隨機(jī)時(shí)鐘延遲時(shí)，尖峰值分布在多個(gè)位置上,，幅值明顯降低,，理論上幅值是峰值的1/32，由于運(yùn)算多為多周期,，同一數(shù)據(jù)保持較長時(shí)間,，加上噪聲等影響，導(dǎo)致實(shí)際效果與理論分析效果有部分差異,；當(dāng)加入64以內(nèi)的延遲時(shí),，差分功耗曲線上沒有明顯的尖峰值出現(xiàn)，達(dá)到了時(shí)間隨機(jī)化抗DPA攻擊的要求,。

4 結(jié)束語

　　本文分析了時(shí)間隨機(jī)化抗DPA攻擊的原理,，結(jié)合ECC處理器的處理特征，設(shè)計(jì)了基于軟中斷的時(shí)間隨機(jī)化電路,。搭建了功耗仿真平臺(tái),，驗(yàn)證了本設(shè)計(jì)的抗DPA攻擊能力。在處理器系統(tǒng)級(jí)進(jìn)行設(shè)計(jì),，與具體的算法無關(guān),，具有較強(qiáng)的通用性,，滿足處理器的抗DPA攻擊需求。

參考文獻(xiàn)

　　[1] Victor Miller.Use of elliptic curves in cryptography[A].In：H.C.Williams.Advances in Cryptography-CRYPTO′85[C].Heidelberg：Springer-Verlag,，1986：417-426.

　　[2] 倪樂.面向橢圓曲線密碼的正規(guī)基模乘單元研究與設(shè)計(jì)[D].鄭州：信息工程大學(xué),，2013.

　　[3] Stefan Mangard，Elisabeth Oswald,，Thomas Popp.能量分析攻擊[M].北京：科學(xué)出版社,，2010.

　　[4] 段二朋，嚴(yán)迎建,，李佩之.針對(duì)AES密碼算法FPGA實(shí)現(xiàn)的CEMA攻擊[J].計(jì)算機(jī)工程與設(shè)計(jì),，2012，33(8)：2926-2930.

　　[5] BUCEK J,，NOVOTNY M.Differential power analysis under constrained budget：low cost education of hackers[C].DigitalSystem Design(DSD),，2013 Euromicro Conference on.IEEE，2013：645-648.

　　[6] 樂大珩.抗能量攻擊的密碼芯片電路級(jí)防護(hù)關(guān)鍵技術(shù)研究[D].長沙：國防科學(xué)技術(shù)大學(xué),，2011.

　　[7] 韓軍.信息安全芯片的防御攻擊技術(shù)研究[D].上海：復(fù)旦大學(xué),，2006.

　　[8] 馬忠梅，馬廣云,，徐英慧,，等.ARM嵌入式處理器結(jié)構(gòu)與應(yīng)用基礎(chǔ)[M].北京：北京航空航天大學(xué)出版社，2002.

　　[9] Darrel Hankerson,，Alfred Menezes,，Scott Vanstone.橢圓曲線密碼學(xué)導(dǎo)論[M].北京：電子工業(yè)出版社，2005.