0 引言

　　作為保障信息安全的重要手段之一，密碼算法在整個信息系統(tǒng)中占有非常重要的地位[1],。隨著用戶對信息安全越來越重視,，加密模式正朝著多協(xié)議配合完成的復(fù)雜加密模式發(fā)展，同時密碼算法也正朝著大位寬,、可重構(gòu)的方向發(fā)展[2],。傳統(tǒng)的單核密碼處理器已經(jīng)無法滿足新型加密模式和復(fù)雜密碼算法日益增長的性能需求。

　　相對于單核處理器而言,，多核處理器可以提供更強的處理能力,。采用多核處理器是解決當(dāng)前復(fù)雜密碼算法實現(xiàn)高性能計算的有效方案[3]。但是當(dāng)前面向密碼操作的專用多核處理器仍沒有相對成熟的設(shè)計技術(shù),。結(jié)合多核處理器設(shè)計技術(shù)和密碼算法硬件實現(xiàn)技術(shù),，設(shè)計一款面向多任務(wù)密碼算法的多核密碼處理器，不僅能夠有效滿足信息安全領(lǐng)域日益增長的需求,，同時也有一定的理論研究價值,。

　　本文基于多任務(wù)密碼算法并行處理特點與多核互連結(jié)構(gòu)設(shè)計技術(shù)，分析了密碼算法處理特征,，提出了密碼多核處理器性能模型,，設(shè)計了符合密碼算法的密碼多核處理器互聯(lián)結(jié)構(gòu)，并與通用多核處理器中廣泛使用的2D-Mesh互聯(lián)結(jié)構(gòu)在密碼算法執(zhí)行性能方面進行了對比,。

1 密碼算法并行化分析及Amdahl定律的擴展

　　密碼算法數(shù)據(jù)處理結(jié)構(gòu)與數(shù)據(jù)處理過程具有不同于通用計算任務(wù)的特殊性,，設(shè)計與密碼處理特征相吻合的多核處理器互聯(lián)結(jié)構(gòu)勢必能夠提高密碼的處理性能[4],。本文研究和分析了密碼多核處理模型，為實現(xiàn)密碼多核處理器互聯(lián)結(jié)構(gòu)的優(yōu)化設(shè)計奠定基礎(chǔ),。

　　1.1 密碼算法統(tǒng)計分析

　　本文針對典型的對稱密碼算法的執(zhí)行過程進行統(tǒng)計分析,，分析結(jié)果如表1所示。

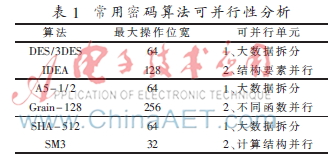
　　由分析結(jié)果可得如下結(jié)論：

　　(1)無論是分組算法,、雜湊算法還是序列算法,，其結(jié)構(gòu)要素內(nèi)部均存在大量的數(shù)據(jù)并行性可開發(fā)，其主要表現(xiàn)為大操作位寬下的小位寬操作并行執(zhí)行,。

　　(2)對稱密碼算法的不同結(jié)構(gòu)要素間存在一定的數(shù)據(jù)并行性,。例如分組密碼算法中，結(jié)構(gòu)要素間的數(shù)據(jù)并行性體現(xiàn)為各子塊數(shù)據(jù)在同一算法執(zhí)行階段可執(zhí)行不同類型的基本操作,。在序列密碼算法的不同結(jié)構(gòu)要素中,，反饋移位寄存器的更新函數(shù)和密鑰流生成函數(shù)表現(xiàn)為當(dāng)前時刻FSR狀態(tài)序列中部分狀態(tài)的不同函數(shù)，可以同時并行執(zhí)行,。鐘控型和結(jié)構(gòu)可變性的序列密碼算法,，其鐘控/結(jié)構(gòu)控制信號和密鑰流生成函數(shù)，表現(xiàn)為某時刻一個或多個反饋移位寄存器狀態(tài)序列中相關(guān)狀態(tài)位的不同函數(shù)可以并行計算,?；诜纸M原理設(shè)計的序列算法的FSR反饋函數(shù)的計算過程各操作間可并行計算。

　　由分析可知,，密碼算法在數(shù)據(jù)處理過程及數(shù)據(jù)處理特征上具備并行處理潛能,，符合多核處理器并行處理特征。因此,，可以通過設(shè)計密碼多核處理器來提升密碼算法的實現(xiàn)效率,。

　　1.2 Amdahl定律分析及推論

　　Amdahl定律是研究如何提升系統(tǒng)性能的經(jīng)典定律[5]。定律指出加快某部件執(zhí)行速度所獲得的系統(tǒng)性能提升受限于該部件在系統(tǒng)中被使用的頻率或所占總執(zhí)行時間的比例[6],。

　　由Amdahl定律可以確定系統(tǒng)中影響性能最大的部件,，同時也可以衡量由于改進某些部件而獲得的系統(tǒng)性能的提高[7]。假設(shè)改進系統(tǒng)某一部件,，那么系統(tǒng)的性能提升比就是：

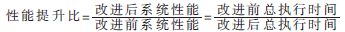
　　通過分析系統(tǒng)性能提升比的公式可知,，影響系統(tǒng)性能提升比的兩個主要因素為：(1)系統(tǒng)完成某任務(wù)的總時間中待改進部分的執(zhí)行時間所占總時間的比重，記為f,；(2)待改進部分改進后比改進前性能提高的倍數(shù),，記為n?；谏鲜龇治隹梢缘贸鋈缦峦普摚?/p>

　　推論1：設(shè)T0為系統(tǒng)改進前完成整個任務(wù)的總時間,。改進后完成整個任務(wù)的時間Tn為：

　　其中，(1-f)表示不可改進部分,。當(dāng)f=0時,，Sp為1,，即沒有可改進部分。當(dāng)n→∞時,，即可獲得的性能改善的極限值受到f的約束,。

　　推論3：改進后被改進部件執(zhí)行時間占系統(tǒng)總運行時間比f′為：

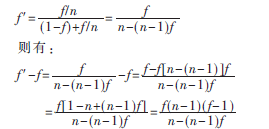
　　當(dāng)f′-f<0時，說明被改進部件在改進后的執(zhí)行時間占系統(tǒng)運行時間比相較于改進前要少,。

2 密碼多核處理器互聯(lián)結(jié)構(gòu)研究與設(shè)計

　　2.1 密碼多核處理器模型研究

　　密碼算法映射在多核處理器上時,，在假設(shè)映射的任務(wù)量是固定的情況下，處理器完成該固定任務(wù)量所需的時間越少則系統(tǒng)性能越高[8],。設(shè)任務(wù)工作量為W,，W由W1，W2,，W3…WM組成,，其中Wi表示并行度為i的任務(wù)工作量，M表示任務(wù)工作量中最大的并行度,，則任務(wù)工作量W可表示為W=wi,。當(dāng)系統(tǒng)有無限多個運算核心，且核心間無通信延遲時,，完成Wi所需時間為ti=Wi/(·i),，其中為單個運算核心的運算能力。由Amdahl定律擴展推論1可知,，完成W的時間為：

　　事實上，密碼多核處理器系統(tǒng)不可能集成無限多個密碼運算核心,。當(dāng)密碼運算核心數(shù)目為N,、任務(wù)工作量并行度為i，單個密碼運算核心的運算能力為時,，且N>i時,，多核系統(tǒng)完成Wi工作量的時間ti=Wi/(·i)；當(dāng)N<i時,，多核系統(tǒng)完成Wi工作量的時間ti=(Wi/(·i))·「i/N,。

　　并行計算中運算核心間存在通信延遲，設(shè)完成Wi工作量的通信延遲為tdi,，此時多核系統(tǒng)完成W工作量所需時間為：

　　通信時間消耗與通信任務(wù)量及通信網(wǎng)絡(luò)結(jié)構(gòu)有關(guān),，而通信任務(wù)量是與任務(wù)并行度i及計算任務(wù)Wi的函數(shù)[9]。設(shè)密碼處理任務(wù)為Wi,，任務(wù)并行度為i,，N個密碼運算核心的多核系統(tǒng)內(nèi)單位時間可傳輸?shù)臄?shù)據(jù)量為Pd=(N)，并行度為i時通信/計算比為(i),，則通信任務(wù)總量Wdi=(i)Wi,，且：

　　同樣,，考慮密碼多核系統(tǒng)集成的計算核心數(shù)N可能小于密碼算法中的任務(wù)并行度i，式(3)修訂為：

　　式(5)給出了適用于密碼多核處理器的結(jié)構(gòu)模型,。式(5)中,，參數(shù)為常數(shù)；當(dāng)密碼應(yīng)用確定時,，參數(shù)Wi為固定值,；多核密碼處理器結(jié)構(gòu)確定時(N)為固定值；(i)與處理器結(jié)構(gòu)及密碼應(yīng)用有關(guān)[10],。

　　2.2 模型參數(shù)分析

　　由2.1節(jié)推導(dǎo)模型可知,，密碼任務(wù)并行度及并行部分所占比例決定了密碼處理器可達到的最高性能，通信延遲是影響密碼多核處理器實現(xiàn)性能的主要因素之一,。在設(shè)計面向該模型的密碼多核處理器時,，應(yīng)該首先分析密碼應(yīng)用的可開發(fā)并行度，初步確定系統(tǒng)運算核心數(shù)目,，然后設(shè)計互聯(lián)結(jié)構(gòu)等,。設(shè)計互聯(lián)結(jié)構(gòu)時注意使?追(N)及?滓(i)盡量小，最后根據(jù)設(shè)計對N值微調(diào)直至最優(yōu),。

　　表2給出了常見密碼算法并行度的統(tǒng)計結(jié)果,。由表2的統(tǒng)計結(jié)果分析可知：密碼應(yīng)用的特點是數(shù)據(jù)運算比較整齊，并行度變化較少,。密碼算法內(nèi)并行度一般為i=1,、2、4,、8,、16，例如AES輪運算并行度i取值為1或4(S盒可開發(fā)i=16并行度),，DES輪運算并行度i取值為1或8,，IDEA輪運算并行度i取值為1或4，MD5輪運算并行度i取值為1或4,。對于密碼協(xié)議等應(yīng)用,，通過對數(shù)據(jù)包的拆分，并行度理論上可以達到無限大,，考慮此類問題,，設(shè)大整數(shù)X作為可實現(xiàn)的最大并行度。

　　為方便研究,，引入簡化條件對多核密碼處理器模型做定性分析,。假設(shè)當(dāng)i≠1，i≠2，i≠4,，i≠8,，i≠16，i≠X時Wi=0,。式(5)可化簡為：

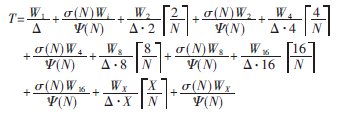
　　由公式分析可知,，影響密碼多核處理器運算效率的主要因素為密碼算法并行度i、通信/計算比?滓(i),、系統(tǒng)單位時間內(nèi)可傳輸數(shù)據(jù)量(N),。其中密碼算法并行度由算法本身決定，通信/計算比(i)由密碼算法及算法任務(wù)映射共同決定,。本文僅討論多核處理器中互聯(lián)方式對多核系統(tǒng)通信性能的影響,，即對系統(tǒng)單位時間內(nèi)可傳輸數(shù)據(jù)量(N)的影響。

　　2.3 簇狀層次化多核互聯(lián)結(jié)構(gòu)設(shè)計

　　假設(shè)密碼算法中并行度i與通信/計算比(i)為固定參數(shù),。此時,，通信性能主要由傳遞延遲決定，設(shè)系統(tǒng)互連結(jié)構(gòu)里消息傳遞過程中跳步數(shù)為H(N),，消息經(jīng)過每個互聯(lián)節(jié)點的延遲為tdc,，則一次通信所需時間tdi=H(N)·tdc。一次通信所完成的工作量Wdc與通信位寬為m bit,、一次可傳輸n個數(shù)據(jù)有關(guān),，即一次通信完成的工作量Wdc(N)=mn。推導(dǎo)可得：

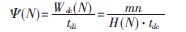
　　m與n的設(shè)計既要考慮硬件實現(xiàn)過程布局布線工藝又要考慮密碼算法任務(wù)間通信量,。據(jù)統(tǒng)計密碼算法中任務(wù)間通信一般為32 bit的整數(shù)倍,。同時考慮工藝技術(shù)，核間通信一般采用32位寬進行通信,。因此系統(tǒng)單位時間內(nèi)可傳輸數(shù)據(jù)量?追(N)的大小主要受通信延遲tdi影響,，tdi又主要由核心間跳數(shù)H(N)與互聯(lián)節(jié)點中轉(zhuǎn)延遲tdc決定。

　　本文結(jié)合現(xiàn)有多核互聯(lián)結(jié)構(gòu)設(shè)計技術(shù),，通過減少多核系統(tǒng)內(nèi)運算核心間跳步數(shù)的方法，優(yōu)化設(shè)計2D-Mesh結(jié)構(gòu),。

　　對于傳統(tǒng)2D-Mesh結(jié)構(gòu)而言,，因為運算核心平鋪在一個平面，隨著多核系統(tǒng)的不斷擴展,，運算核心間數(shù)據(jù)交互跳數(shù)逐漸增多,。由文獻[11]可知，傳統(tǒng)2D-Mesh結(jié)構(gòu)中消息的平均跳步數(shù)H(N)為H(N)=(2)/3,。因此本文在保留相同數(shù)目密碼運算核心前提下,，針對如何降低運算核心間跳數(shù)的問題進行優(yōu)化設(shè)計。

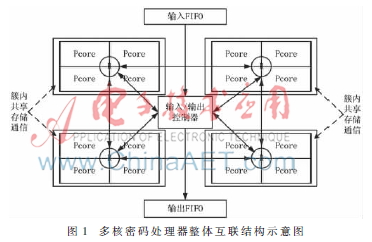
　　本文采用如圖1所示的簇狀層次化多核結(jié)構(gòu)設(shè)計密碼多核處理器。在整個多核系統(tǒng)內(nèi)部建立了三層結(jié)構(gòu)的立體多核系統(tǒng),。最底層分布著密碼運算核心（標記為PCore的一層）,，負責(zé)基本的密碼運算操作。中間層分布著路由節(jié)點（標記為R的一層）,，負責(zé)將最底層運算核間所交付的通信數(shù)據(jù)進行整個多核結(jié)構(gòu)的傳輸,。最高層為多核系統(tǒng)對外接口層(標記為輸入/輸出控制器的一層)，負責(zé)將路由節(jié)點層與外界的數(shù)據(jù)交互,。

　　在該多核系統(tǒng)中,，路由節(jié)點層的路由節(jié)點在連接過程中不再采用路由節(jié)點與運算核心一一對應(yīng)的鏈接關(guān)系，而是采用一個路由節(jié)點掛接四個運算處理核心的方式,，以此減少運算核心在整個多核系統(tǒng)內(nèi)部數(shù)據(jù)交互的跳數(shù),。同時，輸入/輸出控制器也采用同樣的方式鏈接路由節(jié)點,，以改善多核系統(tǒng)外部與多核系統(tǒng)內(nèi)部數(shù)據(jù)交互的跳數(shù),。

　　本文設(shè)計的層次化2D-Mesh結(jié)構(gòu)保留了簇狀2D-mesh結(jié)構(gòu)的優(yōu)點，同時利用輸入/輸出控制器增強了簇單元與高層網(wǎng)絡(luò)通信的靈活性,。實現(xiàn)了處理核單元內(nèi)部通信與外部通信的分離,，為有序、高效的通信提供了結(jié)構(gòu)上的支持,。

3 性能評估

　　根據(jù)1.2節(jié)中Amdahl定律分析結(jié)論,，對比改進后與改進前系統(tǒng)執(zhí)行效率即可衡量系統(tǒng)性能的提升?；诖?，本文將并行部分所占比重不同的并行度為4、8,、16的密碼算法分別映射在本文設(shè)計的簇狀層次化密碼多核結(jié)構(gòu)與2D-Mesh多核密碼處理結(jié)構(gòu)上,，對其執(zhí)行時間進行對比。對比結(jié)果如圖2～圖4所示,。

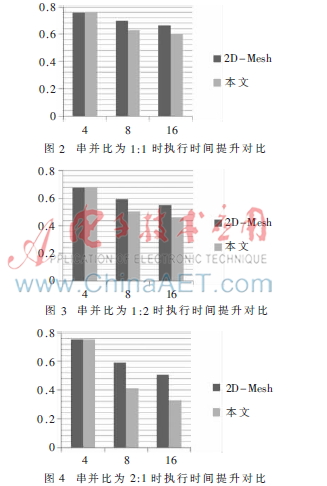
　　由圖2可知,，在多核系統(tǒng)中運算核心數(shù)目（橫軸）確定的情況下，改進后的密碼多核系統(tǒng)相比于改進前在執(zhí)行相同任務(wù)映射的密碼算法時所需時間（縱軸）較少,，即運算效率越高,。在圖3、圖4中,，映射不同串并比的密碼算法也可得到相同結(jié)論,。

　　通過上述對比可知，隨著運算核心數(shù)目的不斷擴展,，本文提出的簇狀層次化多核互聯(lián)結(jié)構(gòu)能夠有效提升多核系統(tǒng)運算效率,，明顯減少了系統(tǒng)內(nèi)部運算核心間通信過程中傳遞延遲，達到了預(yù)期設(shè)計目標。

4 結(jié)束語

　　針對密碼多核處理器設(shè)計,，本文深入研究了對稱密碼算法的并行實現(xiàn)特征,，利用Amdahl定律推導(dǎo)建立符合密碼并行運算特征的多核處理器模型。通過參數(shù)分析,，仿真得到硬件實現(xiàn)的理論依據(jù),。最后依據(jù)理論結(jié)合設(shè)計實際，本文提出了基于2D-Mesh擴展結(jié)構(gòu)的簇狀層次化多核處理器互聯(lián)結(jié)構(gòu),。

　　通過與其他同類設(shè)計相比,，本文設(shè)計的密碼多核處理器互聯(lián)結(jié)構(gòu)具有較高的密碼算法適應(yīng)性和較高的密碼處理性能。在統(tǒng)一的可重構(gòu)密碼多核處理器下不僅實現(xiàn)了對公開對稱密碼算法密碼處理性能的有效加速,，而且還可以支持幾乎所有其他同類密碼算法,。

參考文獻

　　[1] 張曉豐，樊啟華,，程紅斌.密碼算法研究[J].計算機技術(shù)與發(fā)展,，2006，16(2)：179-180.

　　[2] HENNESSY J L,，PATTERSON D A.Computer architecture：a quantitative approach[M].Elsevier,，2012.

　　[3] YU Z，YOU K,，XIAO R,，et al.An 800 MHz 320 mW 16-core processor with message-passing and shared-memoryinter-core communication mechanisms[C].Solid-State Cir-cuits Conference Digest of Technical Papers(ISSCC)，2012IEEE International,，2012：64-66.

　　[4] KHANYILE N P,，TAPAMO J R，DUBE E.An analyticmodel for predicting the performance of distributed applica-tions on multicore clusters[J].IAENG International Journalof Computer Science,，2012.

　　[5] AMDAHL G M.Validity of the single processor approach toachieving large scale computing capabilities[C].Proceedingsof spring joint computer conference.ACM,，1967：483-485.

　　[6] 陳書明，陳勝剛,，尹亞明.Amdahl 定律在層次化片上多核處理器中的擴展[J].計算機研究與發(fā)展,，2012，49(1)：83-92.

　　[7] HILL M D,，MARTY M R.Amdahl's law in the multicoreera[J].Computer,，2008(7)：33-38.

　　[8] BOSSUET L，GRAND M,，GASPAR L，et al.Architectures offlexible symmetric key crypto engines—a survey：Fromhardware coprocessor to multi-crypto-processor system onchip[J].ACM Computing Surveys(CSUR),，2013,，45(4)：41.

　　[9] BLAKE G，DRESLINSKI R G，MUDGE T.A survey ofmulticore processors[J].Signal Processing Magazine,，IEEE,，2009，26(6)：26-37.

　　[10] 李文石,，姚宗寶.基于阿姆達爾定律和蘭特法則計算多核架構(gòu)的加速比[J].電子學(xué)報,，2012，40(2)：230-234.

　　[11] GRAND M,，BOSSUET L,，GOGNIAT G，et al.A reconfig-urable multi-core cryptoprocessor for multi-channel com-munication systems[C].Parallel and Distributed ProcessingWorkshops and Phd Forum(IPDPSW),，2011 IEEE Interna-tional Symposium on,，2011：204-211.