0 引言

　　隨著通信業(yè)務(wù)的高速發(fā)展,，無(wú)線電頻譜的低端頻率已趨于飽和,，頻譜資源匾乏的問(wèn)題日益嚴(yán)重[1],。為了解決頻譜利用率的問(wèn)題,，Joseph Mitola于1999年在軟件無(wú)線電的基礎(chǔ)上提出了認(rèn)知無(wú)線電的概念[2],。要實(shí)現(xiàn)動(dòng)態(tài)頻譜接入，首先要解決的問(wèn)題就是如何檢測(cè)頻譜空穴,，也就是頻譜感知技術(shù),。傳統(tǒng)頻譜感知的解決方案主要有數(shù)字和模擬兩類(lèi)，常見(jiàn)的模擬方式類(lèi)似實(shí)驗(yàn)室的掃描機(jī)制,，需要可調(diào)的線路和獨(dú)立的認(rèn)知無(wú)線電接收設(shè)備。數(shù)字的形式要求采樣率滿足奈奎斯特采樣定理，當(dāng)工作在寬帶環(huán)境下,，采樣率可能會(huì)相當(dāng)大。所以寬帶信號(hào)頻譜感知的難點(diǎn)主要在于現(xiàn)有硬件設(shè)備的模數(shù)轉(zhuǎn)換和信號(hào)處理能力尚無(wú)法滿足對(duì)寬帶信號(hào)需求的高速增長(zhǎng),。因此寬帶信號(hào)頻譜感知的研究將主要集中在如何利用寬帶信號(hào)的稀疏特性通過(guò)較低的采樣率獲得寬帶信號(hào)的部分信息進(jìn)行頻譜感知[3],。認(rèn)知無(wú)線電的廣泛應(yīng)用要建立在創(chuàng)新的頻譜感知技術(shù)上,。

　　本文提出一種基于稀疏傅里葉變換（Sparse Fourier Transform,，SFT）的頻譜感知方法，尤其適用于寬帶認(rèn)知無(wú)線電,。系統(tǒng)結(jié)構(gòu)有兩個(gè)優(yōu)點(diǎn),，一是模擬前端是固定的，不涉及掃描硬件,；二是模數(shù)轉(zhuǎn)換器和數(shù)字信號(hào)處理采樣率都低于奈奎斯特率,。稀疏快速傅里葉變換的算法最早于2012年由MIT的研究人員提出[4],。利用稀疏傅里葉變換的算法,，數(shù)據(jù)流的處理速度會(huì)比快速傅里葉變換還要快10～100倍,，用在頻譜感知這樣海量大數(shù)據(jù)處理方面更能凸顯其優(yōu)勢(shì),。

1 傳統(tǒng)頻譜感知模型

　　最初對(duì)于寬帶信號(hào)檢測(cè)的研究都集中在窄帶頻譜檢測(cè)方面,，每個(gè)節(jié)點(diǎn)在一個(gè)檢測(cè)周期內(nèi)只能檢測(cè)一個(gè)窄帶信道，在完成此次檢測(cè)任務(wù)后才能進(jìn)入下一個(gè)信道的檢測(cè),。這樣對(duì)于單個(gè)認(rèn)知無(wú)線電用戶(hù)來(lái)說(shuō),，不但需要有精確的檢測(cè)性能,，而且需要很長(zhǎng)的檢測(cè)時(shí)間才能完成寬帶范圍內(nèi)的頻譜空閑檢測(cè),。2008年11月的IEEE Signal Processing Magazine綜述了現(xiàn)有的認(rèn)知無(wú)線電技術(shù)[5]。根據(jù)文獻(xiàn)[6]將當(dāng)前的頻譜感知方法總結(jié)在表1中,。

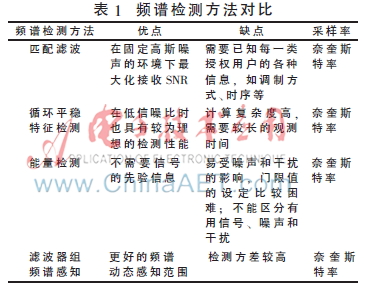
　　單節(jié)點(diǎn)的窄帶頻譜檢測(cè)由于使用條件的不同，在不同的環(huán)境下檢測(cè)性能會(huì)有比較大的變化,。為了適應(yīng)無(wú)線移動(dòng)通信寬帶化的發(fā)展趨勢(shì),，又提出了多節(jié)點(diǎn)協(xié)同寬頻帶檢測(cè)機(jī)制。每個(gè)節(jié)點(diǎn)由多條射頻電路組成,，需要多個(gè)帶通濾波器,，每條窄帶鏈路采用簡(jiǎn)單的能量檢測(cè)算法。但是節(jié)點(diǎn)的硬件電路一旦固定,，各個(gè)濾波器的范圍就隨之固定,。因此這種方法只適用于各個(gè)子頻帶預(yù)先知道并且固定的情況，即需要知道足夠的先驗(yàn)信息,，對(duì)于子信道分配的先驗(yàn)信息未知的情況則無(wú)能為力。

2 基于稀疏傅里葉變換的頻譜感知模型

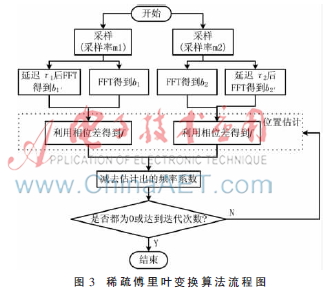
　　傳統(tǒng)的方法需要的采樣率過(guò)高,，無(wú)法真正滿足動(dòng)態(tài)檢測(cè)寬帶頻譜的要求,。本文的頻譜感知模型如圖1所示。利用SFT的思想采用低于傳統(tǒng)奈奎斯特采樣率的方式直接對(duì)寬帶信號(hào)進(jìn)行低速采樣,，并重建原寬帶信號(hào)頻譜,。

　　介紹采樣算法之前，首先介紹一下傅里葉變換的基本特性：信號(hào)時(shí)域的二次抽樣引起頻域的混疊,，圖2證明了這種特性,。對(duì)圖2左上圖時(shí)域的二次抽樣產(chǎn)生了左下圖。在頻域,，二次抽樣后信號(hào)的快速傅里葉變換（Fast Fourier Transform,，F(xiàn)FT）是原信號(hào)FFT的混疊，也就是說(shuō)樣點(diǎn)6和1疊加,，7和2疊加,，以此類(lèi)推。稀疏傅里葉變換的算法主要分為混疊濾波,、估計(jì)和沖突檢測(cè)三步,。下面重點(diǎn)解釋這三步。

　　2.1 混疊濾波

　　為了降低采樣率,，以抽樣因子p對(duì)時(shí)域進(jìn)行二次抽樣,，通過(guò)時(shí)域的抽樣達(dá)到頻域混疊的效果,。因?yàn)轭l域是稀疏的，所以混疊后只有少數(shù)頻率分量上的值非零,。x是長(zhǎng)為N的離散時(shí)間信號(hào)，X是它的頻域表示,。x′是x抽樣后的信號(hào),，其中x=xi×N/B，B可以整除N,。那么X′就是抽樣后的x′的FFT：

　　因此,，混疊是抽樣后進(jìn)行FFT的一個(gè)結(jié)果，頻率等間隔B被分配到同一個(gè)頻率單元上,，例如f將會(huì)分到桶i=f mod B,。另外，每一個(gè)頻率單元的值是所有映射到其中的頻率值的總和,。

    2.2 頻率估計(jì)

　　如果混疊濾波后一個(gè)非零頻率和多個(gè)零值頻率映射到同一個(gè)頻率單元,，則認(rèn)為不發(fā)生沖突，此時(shí)無(wú)法確定非零頻率的具體位置f,。為了計(jì)算f,，利用FFT的相位旋轉(zhuǎn)屬性，即時(shí)域的移位會(huì)轉(zhuǎn)換為頻域的相位旋轉(zhuǎn),。在輸入信號(hào)移位個(gè)采樣點(diǎn)后重復(fù)整個(gè)混疊的過(guò)程,。由于時(shí)域的延時(shí)轉(zhuǎn)換為頻域的相位旋轉(zhuǎn)。相位改變?yōu)椋?/p>

　　因此,，利用相位差即可求出非零頻率的位置f,，這個(gè)過(guò)程稱(chēng)為估計(jì)。對(duì)于所有不發(fā)生沖突的頻率單元,，估計(jì)出原頻譜中非零頻率的位置和頻率值,，也就是f和對(duì)應(yīng)的Xf。

　　2.3 沖突解決和檢測(cè)

　　如果混疊的過(guò)程中兩個(gè)及以上的非零頻率映射到同一個(gè)頻率單元?jiǎng)t稱(chēng)為沖突,。同樣利用FFT的相位旋轉(zhuǎn)屬性可以檢測(cè)是否有沖突發(fā)生,。如果不發(fā)生沖突，則一個(gè)頻率單元中映射進(jìn)來(lái)的頻率僅僅有一個(gè)非零頻率f,，在兩次延時(shí)不同的混疊過(guò)程中的頻率單元的值通過(guò)比較延時(shí)前和延時(shí)后的幅值是否相同,，可以判斷是否發(fā)生沖突。

　　檢測(cè)出沖突后,，可以對(duì)互質(zhì)采樣的混疊濾波進(jìn)行解決,。證明只要采用互質(zhì)的采樣間隔隨機(jī)化混疊時(shí)的頻率位置，就可以防止同一個(gè)頻率對(duì)在兩次混疊中都發(fā)生沖突,。然后在兩次混疊過(guò)程間迭代就可以找到所有的非零頻率,。SFT的具體流程圖如圖3所示,。

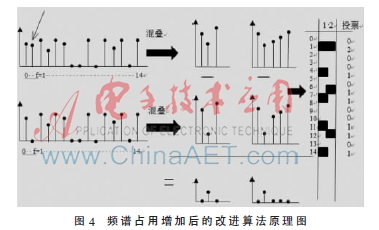
　　由于稀疏傅里葉變換要求應(yīng)用在頻譜占用率不超過(guò)10%的情況，當(dāng)頻譜占用率增加到大于10%后,，不能再采用這種方法進(jìn)行頻譜的稀疏恢復(fù),。但是因?yàn)橐欢螘r(shí)間內(nèi)一個(gè)地區(qū)的頻譜占用情況不會(huì)經(jīng)常發(fā)生變化，可以認(rèn)為在當(dāng)前觀察的時(shí)間窗和下一時(shí)間窗內(nèi)頻譜的變化是稀疏的,，利用這個(gè)頻譜變化的稀疏性進(jìn)行稀疏傅里葉變換,。由于此時(shí)能量發(fā)生變化，不能再利用相位循環(huán)來(lái)找到變化的頻率位置,，考慮在兩次混疊濾波后相減找到變化的頻率混疊后的位置,，然后采用投票的方式判斷出最終狀態(tài)發(fā)生變化的頻率位置。將每次可能映射到其中的頻率位置做個(gè)投票,，如果某頻率位置在兩次混疊后都獲得了投票,，則認(rèn)為此頻率位置為恢復(fù)后的變化頻率位置。算法原理圖如圖4所示,。

3 算法性能仿真

　　為了驗(yàn)證稀疏傅里葉變換用于寬帶頻譜感知的性能,，利用MATLAB平臺(tái)進(jìn)行仿真分析。首先頻譜稀疏信號(hào)采用以下形式產(chǎn)生：

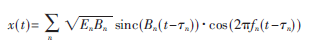
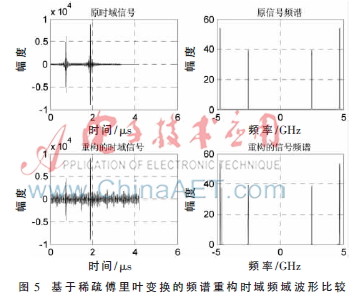
　　其中En,、Bn,、fn、n分別代表第n個(gè)頻帶的能量系數(shù),、帶寬,、載波頻率和延遲時(shí)間。為了仿真實(shí)際采樣過(guò)程,，用2倍奈奎斯特率的離散信號(hào)來(lái)表示連續(xù)信號(hào),，利用抽取的方法實(shí)現(xiàn)濾波后的采樣過(guò)程。采樣5 GHz的信號(hào)至少需要10 GHz的采樣率,，而使用稀疏傅里葉變換需要的采樣率為420 MHz和500 MHz(抽樣因子為21和25,，則可觀測(cè)帶寬為10.5 GHz)。圖5給出了該算法重構(gòu)前后信號(hào)的時(shí)域和頻域形式,。如圖所示,，時(shí)域和頻域的重構(gòu)結(jié)果均較好地再現(xiàn)了原信號(hào)的波形和頻譜，說(shuō)明在信號(hào)頻譜相對(duì)稀疏的情況下,，稀疏傅里葉變換可以較好地進(jìn)行頻譜檢測(cè),。

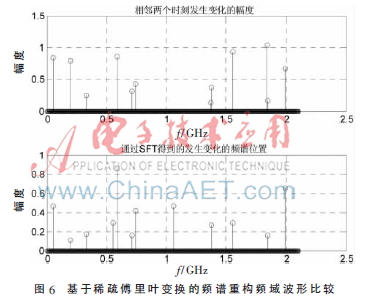
　　當(dāng)頻譜的占用增加到50%時(shí)，時(shí)間窗長(zhǎng)度為10 s,，假設(shè)狀態(tài)發(fā)生變化的頻率分量占總數(shù)的3%,，利用改進(jìn)算法成功恢復(fù)出狀態(tài)發(fā)生變化的頻率位置如圖6所示。由于只關(guān)心頻譜是否被占用,，而不關(guān)心具體的頻率幅度,，所以認(rèn)為改進(jìn)的算法可以成功地找到變化的頻率位置,。

4 算法性能評(píng)估

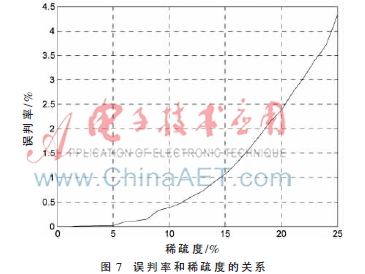
　　誤判率：占有頻率被SFT判斷為空閑的百分比。對(duì)于不同稀疏性的情況下,，仿真得到誤判率和稀疏性的關(guān)系如圖7所示,。可以看出在稀疏度小于10%時(shí),，誤判率不超過(guò)0.5%,，當(dāng)稀疏度高達(dá)25%時(shí)，誤判率也不超過(guò)5%,。

　　運(yùn)算復(fù)雜度：FFT計(jì)算N點(diǎn)DFT時(shí)，其運(yùn)算復(fù)雜度為O(N log2 N),。而SFT只需要4次混疊的過(guò)程,，即其運(yùn)算復(fù)雜度僅為O(2B1log2 B1)+O(2B2log2 B2)。假設(shè)B1>B2,，則復(fù)雜度為O(B1log2 B1),。當(dāng)N比較大時(shí)，SFT的效率提高更加明顯,。

　　采樣率：直接對(duì)一個(gè)5 GHz信道進(jìn)行寬帶信號(hào)頻譜檢測(cè)需要10 GHz的采樣率,，而使用SFT可以使用500 MHz和420 MHz的采樣率，采樣率大約降低到原來(lái)的20%,，硬件上易于實(shí)現(xiàn),，且效率更高。

5 結(jié)論

　　本文通過(guò)分析傳統(tǒng)頻譜感知方式的不足,，提出了一種基于稀疏快速傅里葉變換的寬帶頻譜感知方法,。該方法能夠以若干低速ADC完成對(duì)寬帶頻譜信號(hào)的采樣，解決了寬帶頻譜感知中采樣速率過(guò)高的問(wèn)題,，為亞奈奎斯特采樣的寬帶頻譜感知提供了一種新的思路,。

參考文獻(xiàn)

　　[1] Mishali Moshe，Eldar Yonina C.Wideband spectrum sensing at sub-nyquist rates[J].IEEE Signal Processing Magazine,，2011,，28(4)：102-135.

　　[2] 蓋建新，付平,，喬家慶,，等.用于寬帶頻譜感知的全盲亞奈奎斯特采樣方法[J].電子與信息學(xué)報(bào)，2012,，34(2)：361-367.

　　[3] Ahmad B I,，Al-Ani M，Tarczynski A,，et al.Compressive and non-compressive reliable wideband spectrum sensing atsub-Nyquist rates[C].Signal Processing Conference(EUSIPCO),，2013 Proceedings of the 21st European IEEE,，2013：1-5.

　　[4] HASSANIEH H，SHI L,，ABARI O,，et al.GHz-wide sensingand decoding using the sparse Fourier transform[C].，2014 Proceedings IEEE,，2014：2256-2264.

　　[5] RAMOS S,，F(xiàn)EIJO C，GMEZ-BARROSO J L.Next gen-eration mobile network deployment strategies[J].Journal of the Institute of Telecommunications Professionals,，2009,，3(1)：13-19.

　　[6] GOGGIN G.Adapting the mobile phone：the iPhone and its consumption[J].Continuum: Journal of Media & Cultural Studies，2009,，23(2)：231-244.