摘  要： 因近紅外光譜具有波長點多、譜帶歸屬困難,、光譜重疊嚴重及光譜分布結構未知等問題,，在進行近紅外光譜關鍵特征提取和數(shù)據(jù)特征空間映射時難以準確獲知合適降維方法。為了解決該問題,，本文對比分析了典型線性和非線性降維方法,，并用煙葉近紅外光譜數(shù)據(jù)從數(shù)據(jù)降維可視化和分類準確性識別率角度分別進行了實驗驗證。結果表明,，線性降維算法,，特別是PCA、LDA算法,，比較適合應用于煙葉近紅外光譜降維分析中,，非線性降維算法因其泛化學習能力與推廣能力差以及本征維數(shù)估計困難不適合應用于近紅外光譜降維分析。

　　關鍵詞： 降維,；PCA,；LDA；近紅外光譜,；小樣本

0 引言

　　近紅外光譜（NIR）分析技術是近年來分析化學領域迅猛發(fā)展的高新分析技術,，越來越受到國內(nèi)外分析專家的關注，在分析化學領域被譽為分析“巨人”,。它的出現(xiàn)可以說帶來了又一次分析技術的革命,。近紅外光譜分析技術廣泛應用于農(nóng)產(chǎn)品、化工,、醫(yī)藥等領域的質(zhì)量分析,。然而，由于近紅外光譜數(shù)據(jù)具有高維,、譜帶重疊等特征,，給提取樣品的關鍵主成分信息帶來了一定程度的困難和挑戰(zhàn)。如何實現(xiàn)高維到低維空間的特征映射關系,，選擇合適降維方法顯得尤為重要,。近年來,，為了解決高維光譜數(shù)據(jù)降維問題，國內(nèi)外相繼出現(xiàn)大量的降維算法,。主成分分析（PCA）[1]和線性識別分析（LDA）[2]是目前應用最為廣泛的特征提取與數(shù)據(jù)降維方法之一,。但當分析數(shù)據(jù)集呈現(xiàn)非線性且數(shù)據(jù)分布明顯彎曲時，采用線性降維方法無法獲取數(shù)據(jù)非線性結構特征,。為了更好地解決該問題,，先后有不少非線性降維方法被提出，比較經(jīng)典的有局部線性嵌入LLE算法,、等距離映射方法Isomap算法,；另外，Sammon[3]提出了一種非線性映射,，即Sammon映射（SM）,，該算法能夠保持輸入樣本之間的相關距離；Hastie[4]提出了Principal Curves（PC）,，其定義為通過概率分布或數(shù)據(jù)云中間的“自洽”光滑曲線,；Kohonen[5]基于自組織神經(jīng)網(wǎng)絡提出Self-organizing Map（SOM）用來保存數(shù)據(jù)空間的拓撲屬性；Scholkopf[6]應用Mercer核將PCA擴展為Kernel PCA（KPCA）,，該算法在高維空間中計算主分量,，而該高維空間由輸入空間經(jīng)某種非線性映射得到；Mika等[7]采用相同的思想來非線性擴展LDA,，從而提出了Kernel LDA（KLDA）,。

　　上述這些線性和非線性降維方法各有特性，適合解決不同類型特征數(shù)據(jù),，對于近紅外光譜而言,，需要根據(jù)光譜特征找到適合降維和關鍵特征提取方法，因此,，本文重點分析近紅外光譜特征,，對比分析了線性降維算法與非線性降維算法在提取關鍵數(shù)據(jù)特征方面的優(yōu)缺點，獲得一種可行有效的降維方法,，并在實際應用中得到較好應用,。

1 降維方法

　　1.1 線性降維方法

　　主成分分析PCA是目前應用最為廣泛的降維方法之一。PCA算法依據(jù)的是方差最大化原理,，將數(shù)據(jù)從高維空間向低維空間映射,，并使之投影后方向相互正交。主成分大小根據(jù)方差大小依次提取,。PCA是一種無監(jiān)督的降維算法,，該方法無需考慮數(shù)據(jù)類別屬性，通過某種線性投影變化獲得綜合變換,，綜合變量最大化反應了原始光譜數(shù)據(jù)中所反映的大致規(guī)律,。

　　線性判別式分析LDA算法是模式識別的經(jīng)典算法，其基本思想是將高維的模式樣本投影到最佳鑒別矢量空間,，以達到抽取分類信息和壓縮特征空間維數(shù)的效果,，投影后保證模式樣本在新的子空間有最大的類間距離和最小的類內(nèi)距離，使投影后空間中有最佳的可分離性,。但是,，PCA和LDA方法中的全局線性屬性限制了它們在非高斯分布數(shù)據(jù)上的有效性。

　　1.2 兩種線性方法的區(qū)別

　　PCA算法是在數(shù)據(jù)空間中找出一組向量,，用此向量盡可能地表達數(shù)據(jù)的方差,，將數(shù)據(jù)從高維降到低維，其利用K-L變換獲得逼近原數(shù)據(jù)空間的最低維識別空間,。LDA算法也是一種線性降維方法,，它基于分類的思想對數(shù)據(jù)進行降維，即它希望降維后的數(shù)據(jù)在分類后間距盡可能的大,。

　　1.3 兩種線性方法的結合PCA+LDA

　　根據(jù)PCA與LDA的特點,，可將二者進行結合使用。設訓練樣本為xi∈Rm×n,，i=1,，2，…,，N,，N表示訓練樣本數(shù)，訓練樣本的協(xié)方差矩陣Q為XXT,，然后計算協(xié)方差矩陣的特征值與特征向量,，并取其較大d個特征值對應的特征向量，組成PCA算法的特征子空間W1,；在樣本數(shù)小于樣本維數(shù)時,，直接運用LDA算法會出現(xiàn)小樣本問題，即Sw奇異,，此時無法求出Sw-1Sb的特征向量,，其中Sw為類內(nèi)散布矩陣，Sb為類間散布矩陣,。依據(jù)PCA算法的特征子空間W1,，結合使用PCA、LDA算法時Sw與Sb分別定義為：

　　Sw=W1TXwXwW1

　　Sb=W1TXbXbW1

　　然后,，求解矩陣Sw-1Sb的特征值問題,。這里選擇Sw-1Sb的P個較大特征值對應的特征向量構造LDA算法的特征子空間W2，將PCA算法與LDA算法的特征子空間進行融合,，即WS=W1W2,，可獲得PCA-LDA算法的融合特征空間WS,，使用得到的WS作為PCA-LDA算法的特征空間進行運算。

　　1.4 非線性降維方法

　?。?）LLE算法

　　局部線性嵌入（Locally Linear Embedding,，LLE）算法是流形學習中非線性降維方法中最為經(jīng)典的算法之一，能夠使降維后的數(shù)據(jù)較好地保持原有流形結構,，并找到每個樣本的k個最近鄰域,。

　　（2）ISOMAP

　　如果數(shù)據(jù)采自一個蛋卷形的流形,，兩點間的歐式距離不能真實反應兩點間的關系,，而兩個點之間沿著蛋卷的最短距離即geodesic距離可以更好地反應這兩個點之間的關系。ISOMAP的主要思想就是利用點之間的geodesic距離來代替點之間的歐氏距離,，然后用Metric MDS計量多元尺度算法進行數(shù)據(jù)降維,。ISOMAP對數(shù)據(jù)的整體平移、旋轉(zhuǎn)和翻轉(zhuǎn)具有不變形的特性,，并且它最后也歸結為特征值和特征向量的計算問題,，它具有發(fā)現(xiàn)高維空間低維流形的能力。

　?。?）KPCA（Kernel-PCA）

　　KPCA算法是基于核函數(shù)的思想對PCA算法進行改進,，它不會顯著增加計算的復雜度，并且繼承了PCA算法可以得到全局最優(yōu)解的特性,，另外它可以求解非線性問題,。其算法思想大致如下：假設有m個數(shù)據(jù)x1，x2,，…,，xm，當這些數(shù)據(jù)在n維空間中線性不可分時,，希望通過一個映射將數(shù)據(jù)從n維空間映射到N（N>n）維空間中,，使得數(shù)據(jù)在N維空間中是線性可分的，這樣,，當使用PCA在N維空間對數(shù)據(jù)進行降維時可以得到更好的結果,。實踐發(fā)現(xiàn)，當對數(shù)據(jù)處理時,，經(jīng)常會出現(xiàn)求兩個向量點積的形式,，即椎（xi）T（xj）的形式，于是,，可以用一個函數(shù)來代替這種點積計算,，即尋找一個函數(shù)，使得K（xi，xj）=（xi）T（xj）,，這樣可以把求點積的運算轉(zhuǎn)化為求函數(shù)值的問題,。這里的函數(shù)K（xi，xj）便稱為核函數(shù),。

2 實驗部分

　　2.1 材料和儀器

　　為了獲得有效的近紅外光譜數(shù)據(jù)降維方法,，挑選了134個有代表性的復烤片煙,，包含福建,、云南、山東3個質(zhì)量差異明顯的產(chǎn)區(qū),。這些煙葉樣品的近紅外光譜采用FOSS近紅外分析儀NIRS DS2500采集,，該設備波長范圍400~2 500 nm，數(shù)據(jù)采樣間隔0.5 nm,。

　　2.2 環(huán)境條件

　　為了保證近紅外光譜數(shù)據(jù)采集的準確性和穩(wěn)定性,，需具有良好的環(huán)境溫濕度條件，空氣相對濕度范圍保持20%~70%,，溫度范圍為20℃~26℃,，樣品檢測過程中門窗處于關閉狀態(tài)，確保每小時的溫度變化不大于1℃,，濕度變化不大于2%,。

　　2.3 樣品前處理

　　將挑選的134份來自三個不同產(chǎn)區(qū)的煙葉樣品進行抽樣、去梗等前處理,，然后在烘箱中以60℃,、4 h條件烘干（含水量約為4%~8%），從烘箱中取出烘好的樣品馬上磨粉,，過篩40目,，裝入密封袋中密封并常溫下避光貯存。

　　2.4 光譜數(shù)據(jù)采集

　　每份煙葉粉末樣品稱重20~25 g,，采用漫反射的方式掃描,，每個樣本重復裝樣3次，取平均光譜作為該樣品的最終近紅外光譜,。

　　2.5 實驗驗證分析

　　2.5.1五種降維算法的數(shù)據(jù)可視化結果

　　本實驗中,，分別采用PCA、LDA,、LLE,、ISOMAP、KPCA 5種降維算法對134份煙葉粉末樣品近紅外光譜數(shù)據(jù)在MATLAB平臺下進行降維分析,，降維因子數(shù)為10個,，其獲得數(shù)據(jù)可視化結果如圖1~圖5（其中橫軸表示降維后第一主成分的得分，縱軸表示降維后第二主成分的得分）。

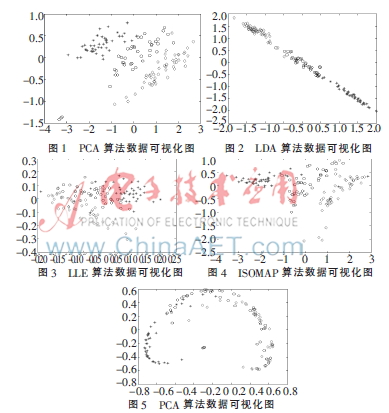
　　從數(shù)據(jù)的可視化結果來看,，LDA算法在水平與垂直方向都可以把產(chǎn)區(qū)分開,，PCA、LLE,、ISOMAP可以在某些方向上把產(chǎn)區(qū)分開,，Kernel-PCA可以在某些區(qū)域內(nèi)把產(chǎn)區(qū)分開。

　　2.5.2 分類結果

　　從降維后的可視化結果中可看出5種算法的不同性能,，此外,，本文從另外一個角度——分類器正確識別率來判斷算法的適合性。從三個產(chǎn)區(qū)中分別隨機選取部分樣本作為測試樣本,，訓練樣本與測試樣本的組成結構如表1所示,。如果測試樣本經(jīng)過分類器分類之后可以正確識別出產(chǎn)區(qū)信息，則認為是正確識別,。實驗過程中主因子數(shù)采用1~10,，對5種降維算法分別進行KNN分類，不同算法采用不同主因子數(shù)得到的正確識別率如表2所示,。

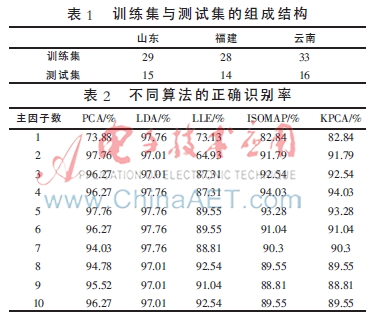
　　由表2可以看出：（1）LDA具有最好的對煙葉產(chǎn)區(qū)分類功能,，其次是PCA和ISOMAP，LLE對于產(chǎn)區(qū)分類的效果不理想,，由此可以推測煙葉近紅外光譜在高維空間的分布情況,；（2）特征空間維數(shù)對產(chǎn)區(qū)的正確識別率有一定的影響，并不是特征空間的維數(shù)越多對產(chǎn)區(qū)分類越好,，這表明在特征提取時部分維數(shù)信息對于產(chǎn)區(qū)的分類是具有干擾性的,。

3 結論

　　本文著重對比分析了線性與非線性的數(shù)據(jù)降維方法在煙葉光譜中的應用。在對5種降維算法的分析中可以看出,，PCA和LDA降維算法在煙葉近紅外光譜圖方面相對其他的降維算法有較好的分類性能,，而且特征空間的維數(shù)對產(chǎn)區(qū)分類有一定的影響，合適的特征空間維數(shù)能夠進行較好的分類,。本文的分析結果與專家評吸的結果相一致,，對降維算法的研究可為實際應用中降維算法的選擇提供重要的參考依據(jù)。

參考文獻

　　[1] HOTELLING H. Analysis of a complex of statistical variables into principal components[J]. Journal of Educational Psychology,， 1933,，24：417-441.

　　[2] FISHER R A. The use of multiple measurements in taxonomic problems[J]. Annals of Eugenics， 1936,，7（2）：179-188.

　　[3] SAMMON J J W. A nonlinear mapping for data structure analysis[J]. IEEE Trans on Computers,，1969，18（5）：401-409.

　　[4] HASTIE T. Principal curves and surfaces[D]. California：

　　Stanford Univ,， 1984.

　　[5] KOHONEN T. Self-organizing Maps[J]. Journal of Mathematical Modelling and Algorithms,，2008，7（4）：371-387.

　　[6] SCHOLKOPF B， SMOLA A,， M?譈LLER K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation,， 1999（10）：1299-1319.

　　[7] MIKA S， RATSCH G,， WESTON J,， et al. Fisher Discriminant Analysis with Kernels[C]. Proc. IEEE Workshop Neural Networks for Signal Processing， 1999,，25： 41-48.