摘 要: EMI的定位測(cè)試是電磁兼容測(cè)試的一個(gè)重要內(nèi)容。傳統(tǒng)的干擾源定位測(cè)試方法相對(duì)大型的電子設(shè)備而言效率和準(zhǔn)確度都有限。本文提出一種基于空間譜估計(jì)技術(shù)的EMI定位方法,該方法使用二維空間平滑算法對(duì)電磁干擾信號(hào)進(jìn)行DOA(波達(dá)方向)估計(jì)從而精確定位電磁干擾源。在MATLAB平臺(tái)上編寫(xiě)了相關(guān)程序進(jìn)行了模擬實(shí)驗(yàn),實(shí)驗(yàn)結(jié)果證明,該方法不僅可以區(qū)分不同頻率的干擾而且可以定位同頻的干擾,可以為實(shí)際應(yīng)用提供參考。
關(guān)鍵詞: EMI;干擾源定位;二維空間平滑;DOA(波達(dá)方向)
0 引言
在電磁兼容現(xiàn)場(chǎng)測(cè)量中,對(duì)電磁干擾源進(jìn)行快速定位可以幫助工程師快速地排除電磁干擾問(wèn)題。傳統(tǒng)的關(guān)于輻射源定位方法是使用輻射信號(hào)的頻率這一信息,根據(jù)所找到的超標(biāo)點(diǎn)頻率去尋找頻率相同的輻射源,但是在一個(gè)大型的電子設(shè)備或者系統(tǒng)中往往可能有多個(gè)位置產(chǎn)生相似頻率的干擾,因此使用這種方法定位干擾源可能會(huì)出現(xiàn)誤差[1]。
在基于自適應(yīng)干擾抵消系統(tǒng)的虛擬暗室中使用信號(hào)的相關(guān)性定位電磁輻射干擾源。其使用兩個(gè)探頭,一個(gè)放在EUT(受試設(shè)備)附近的遠(yuǎn)場(chǎng)天線或者電流卡鉗,一個(gè)作為近場(chǎng)探頭[2]。用兩個(gè)探頭同時(shí)接收EUT輻射出的信號(hào),通過(guò)雙通道的同步接收機(jī)對(duì)接收到的兩個(gè)信號(hào)進(jìn)行處理,并通過(guò)研究?jī)蓚€(gè)信號(hào)的相關(guān)性實(shí)現(xiàn)干擾源的識(shí)別定位。但是基于信號(hào)相關(guān)性的定位方法需要不斷地移動(dòng)接收天線,而且在不同地點(diǎn)接收到的同一輻射信號(hào)也有變化,這都會(huì)影響定位的準(zhǔn)確性。本文提出一種基于空間譜估計(jì)技術(shù)的電磁干擾定位方法,該方法使用二維空間平滑對(duì)電磁信號(hào)進(jìn)行DOA(波達(dá)方向)估計(jì)以精確定位電磁干擾源[3]。二維空間平滑算法可以分辨出不同來(lái)向的相干信號(hào),且具有很高的定位精度,適合用于EMC現(xiàn)場(chǎng)測(cè)量的電磁干擾源定位。
1 基本原理
1.1 MUSIC算法
假設(shè)EMC現(xiàn)場(chǎng)測(cè)量空間中入射到M元陣列的EUT輻射信號(hào)和干擾信號(hào)共計(jì)p個(gè)[4],則陣列接收信號(hào)的協(xié)方差矩陣為:

由于假設(shè)的干擾信號(hào)及EUT輻射信號(hào)與噪聲是不相關(guān)的加性高斯白噪聲,因此在式(1)中的第一項(xiàng)是滿秩矩陣,s是對(duì)角陣,包含了干擾信號(hào)和EUT輻射信號(hào)的特征值。?滓2和Un是協(xié)方差矩陣對(duì)應(yīng)的特征值和特征向量。故:

由于U=[Us,Un]是酉矩陣,其不同特征值對(duì)應(yīng)特征向量之間正交。因此:
UsHUn=0(8)
由式(6)和式(8)知,陣列輸出的方向矩陣A與協(xié)方差矩陣的干擾信號(hào)和EUT輻射信號(hào)特征向量組成的子空間矩陣Us相同。表示為:

噪聲特征值對(duì)應(yīng)的特征向量與信源的方向正交。得到空間譜估計(jì)形式為:
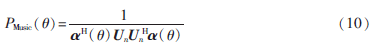
對(duì)PMusic(θ)譜峰θ域?qū)?yōu),所求的θ即為入射信號(hào)的DOA的估計(jì)。
1.2 二維空間平滑算法
MUSIC不能對(duì)空間中相關(guān)的信號(hào)進(jìn)行估計(jì),且只能對(duì)信號(hào)進(jìn)行一維的定位[5]。本文使用二維空間平滑算法對(duì)電磁干擾信號(hào)進(jìn)行定位[6]。如圖1所示的M×N的均勻矩形陣列,分成若干個(gè)重疊大小為m×n的均勻矩形子陣列。
假設(shè)K個(gè)遠(yuǎn)場(chǎng)窄帶信源s(t)照射到這個(gè)矩形陣列上,信號(hào)的俯仰角用陣列的第(m,n)個(gè)陣元的輸出為:

式中:


將圖1所示的M×N的均勻矩形陣列分成若干個(gè)M0×N0的均勻矩形子陣,如圖2所示。

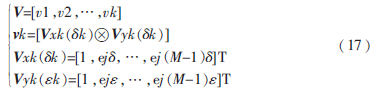
第(m,n)個(gè)子陣的接收信號(hào)向量為:
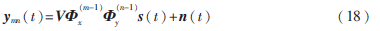
![IKP04ITMXU[D_6JKDT]9HCH.jpg IKP04ITMXU[D_6JKDT]9HCH.jpg](http://files.chinaaet.com/images/2016/02/01/6358994610779700002197761.jpg)
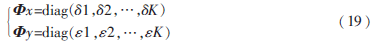
第(m,n)個(gè)子陣的協(xié)方差矩陣為:
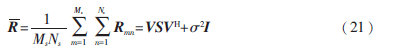
定義所有子陣的協(xié)方差矩陣的平均值為二維空間平滑協(xié)方差矩陣:
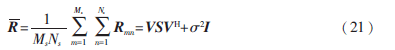
上式中Ms=M-M0+1,Ns=N-N0+1
按照MUSIC的方法對(duì)得到的協(xié)方差矩陣進(jìn)行處理,估計(jì)出空間電磁干擾信號(hào)的來(lái)向。
2 實(shí)驗(yàn)仿真
設(shè)接收陣列為6×6的二維等距平面矩形陣列,在x軸方向和y軸方向上,陣元之間的距離均為d=400 mm。設(shè)空間中有三個(gè)不同體制下的信號(hào),其中一個(gè)為EUT的單頻輻射信號(hào),另外兩個(gè)均是電磁兼容現(xiàn)場(chǎng)測(cè)量現(xiàn)場(chǎng)的環(huán)境干擾信號(hào)或者是受試系統(tǒng)的其他部分發(fā)出的超標(biāo)干擾源。所使用的均為窄帶信號(hào),其數(shù)學(xué)形式為:
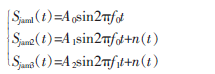
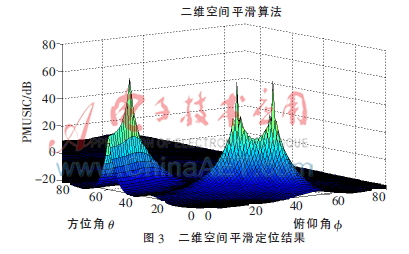
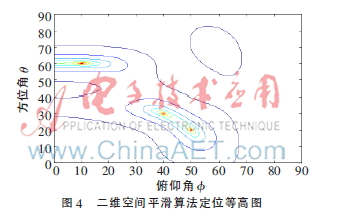
其中,A0=2A1=A2,f0=200 MHz,f1=10 MHz。n(t)是空間中的白噪聲和各個(gè)陣元上的加性噪聲,信噪比為20 dB。其中電磁信號(hào)的水平方位角和俯仰角為[30,40],[20,50],[60,10]。使用MATLAB軟件平臺(tái)對(duì)二維空間平滑算法性能進(jìn)行仿真實(shí)驗(yàn),取子陣為4×4的均勻矩形陣,在快拍數(shù)為500的情況下運(yùn)用改進(jìn)的空間平滑技術(shù)對(duì)空間中同頻信號(hào)和不相關(guān)信號(hào)的估計(jì)結(jié)果如圖3和圖4所示。
3 結(jié)束語(yǔ)
實(shí)驗(yàn)仿真表明,通過(guò)二維空間平滑算法可以精確估計(jì)出空間中電磁信號(hào)的DOA,利用電磁干擾信號(hào)的DOA可以對(duì)大型系統(tǒng)或者電子設(shè)備的干擾源進(jìn)行定位。較傳統(tǒng)的頻率定位法和相關(guān)性定位方法,該測(cè)試方法不僅定位方便而且可以對(duì)相干信號(hào)進(jìn)行定位,因此可以應(yīng)用于大型系統(tǒng)或電子設(shè)備的EMI測(cè)試中。
參考文獻(xiàn)
[1] 容向系統(tǒng)科技有限公司.CASSPER系統(tǒng)技術(shù)文檔[Z].2005.
[2] SCHMIDT R.Multiple emitter location and signal parameter estimation [J]. IEEE Trans on AP,1986,34(3):276-280.
[3] SHAN T J, WAX M, KAILATH T. On spatial smoothingfor direction-of-arrival estimation of coherent signals[J]. IEEE Trans on ASSP, 1985,33(4):806-811.
[4] 劉夢(mèng)南.預(yù)測(cè)試中的噪聲抑制與消除技術(shù)[J].安全與電磁兼容,2003(6):34-41.
[5] 程君佳,田書(shū)林,李力.電磁干擾源的相關(guān)性定位測(cè)試方法研究[J].中國(guó)測(cè)試技術(shù),2007,33(2):42-44.
[6] 魏小麗,陳建,林琳.基于空間平滑算法的二維相干源DOA估計(jì)[J].吉林大學(xué)學(xué)報(bào),2008,38(5):1160-1164.

