摘  要： 為了能夠進一步準確地估計出雷達信號的瞬時頻率,，在原有的Morlet小波基函數(shù)的基礎上,，提出了一種改進的Morlet小波基函數(shù)，并將其用于小波脊線的提取,。用改進后的Morlet小波基函數(shù)來提取雷達信號的小波脊線特征,，從而估計出雷達信號的瞬時頻率。仿真結果表明,，用改進后的Morlet小波基函數(shù)提取出來的雷達特征比利用原有的Morlet小波基函數(shù)提取出來的雷達特征性能更優(yōu),，具有更好的時頻綜合特性及良好的抑制噪聲能力，其方法是可行的,。

　　關鍵詞： 瞬時頻率,；Morlet小波變換；小波脊線

0 引言

　　在電子情報偵察和對抗領域,，能否有效地,、高精度地從被截獲的雷達信號中提取信號的瞬時參數(shù)，對識別信號的“指紋”具有重要的意義[1],。瞬時頻率比瞬時幅度具有更強的抗外界干擾的優(yōu)點,，并且它能夠反映每一時刻雷達信號的頻率變化，因此成了一個研究熱點[2-9],。

　　本文根據(jù)Morlet小波參數(shù)對信號調制特征的影響及對小波脊線理論的分析[2]，提出了一種既有良好的抑制噪聲能力又具有綜合時-頻分辨率較高的小波基函數(shù),，用于小波脊線的提取[3],，并通過小波脊線迭代方法估計信號的瞬時頻率。該方法能夠做到連續(xù)小波變換的最優(yōu)尺度選擇,，比小波變換的模極大值方法更優(yōu),。

1 小波脊線原理

　　小波變換的時頻平面脊線上分布的參數(shù)能用來描述原始信號的重要參數(shù)，因為它與原始信號之間具有很強的相似性,。而信號的頻率與幅度的變化往往由脊線的位置及脊線上分布數(shù)據(jù)的起伏變化決定的[4],。

　　1.1 信號的解析表示

　　數(shù)學上，任意實信號s（t）都可以表示成以下的形式：

　　信號s（t）對應的解析信號可表示為：

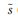　　（t）=s（t）+jsH（t）（2）

　　其中,，sH（t）為信號s（t）的Hilbert變換,，且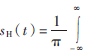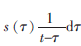。如果s（t）為漸進信號，即信號的幅度變化要遠遠小于信號的瞬時頻率變化,，即：

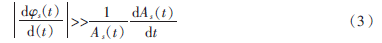
　　則其解析信號可近似表示為：

　　在之后的討論中,，把要分析的信號s（t）限定在實Hardy空間：

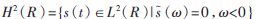
　　1.2 小波脊線

　　若（t）=Aε（t）e為實小波ε（t）的解析形式，則漸進信號s（t）的解析小波變換為：

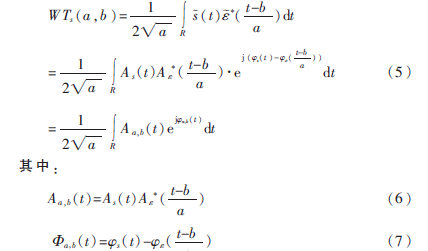
　　式中*表示復數(shù)共軛,。由平穩(wěn)相位原理可知,，駐點ts對積分式起著主要的作用。對于單成分的信號而言,，在信號（t）及小波函數(shù)均為漸進函數(shù)的情況下,，相位?椎a，b（t）關于時間t就僅僅只有一個駐點ts,，即滿足′a,，b（ts）=0且a，b（ts）≠0,。

　　定義小波脊線為：

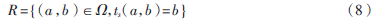
　　根據(jù)駐點的特性,，小波脊線上滿足：

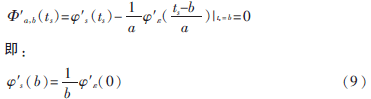
　　顯而易見，尺度a和平移參數(shù)b互為函數(shù)關系,，即有：

　　小波脊線上有式（10）,，式中ar（b）即為小波脊線，可以看出小波脊線是平移參數(shù)b的函數(shù),。由式（10）可知,，通過提取小波脊線就可以完成信號瞬時頻率fr（t）的提取，如式（11）所示：

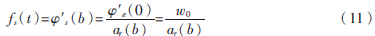
　　其中,，w0為小波基函數(shù)的中心頻率,。

2 小波基函數(shù)的選取

　　為了提取小波脊線，假定信號s（t,，r（t））具有隨r（t）變化的瞬時性,，如果r（t）能夠被小波基函數(shù)g（t）檢測出來，則需要滿足以下3個條件[5-6]：

　?。?）在r（t）=r不存在瞬時變化的情況下,，小波系數(shù)WTs只隨a變化，與b無關,，即L（a）=WTs{a,，t|r}，r為常數(shù),；

　?。?）在t時刻r（t）變化時，WTs{a,，t|r}會產(chǎn)生一個明顯與L（a）不同的值,；

　?。?）在t時刻，為了達到一個相對比較高的檢測頻率,，小波系數(shù)與L（a）的差值D達到最大,，即Dmax=max（|WTs（a，t）-L（a）|）,。

　　由小波脊線檢測條件知,，小波脊線的提取效果與小波基函數(shù)的選擇有直接的關系。

　　2.1 Morlet小波

　　Morlet小波常因為其具有良好的時-頻域特征,，而被選為提取雷達信號特征參數(shù)的小波基函數(shù),，它的表達式為：

　　g1（t）=exp（-t2/N）exp（jw0t）（12）

　　當N=5時，為普通的Morlet小波,，其波形如圖1所示,。

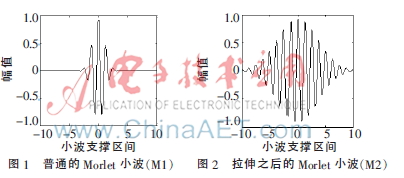
　　當N=25時，波形如圖2所示,，它的傅里葉變換為：

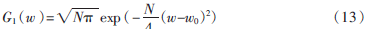
　　母波時頻窗為：

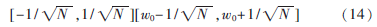
　　子波時頻窗為：

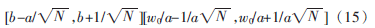
　　由式（15）可知,，小波變換對信號的時頻分辨率受到小波原子尺度a的伸縮的直接影響，而b只是對時頻窗位置的改變,。尺度因子a越小,，時域分辨率越高，頻域分辨力就越低,。為了提高檢測概率,，小波變換通過調節(jié)a的值來滿足?駐w，使時頻分辨率能夠自適應調節(jié),。

　　由式（14）,、（15）知，N的作用主要是協(xié)調時域和頻域的分辨力,，使其都達到最優(yōu)狀態(tài),。N越大，頻率分辨力就越大,，但由于N受到小波變換條件及時域分辨率的約束,，不可能無限制地增大，因此在估計信號瞬時頻率時,，要兼顧時域和頻域。

　　2.2 改進的Morlet小波

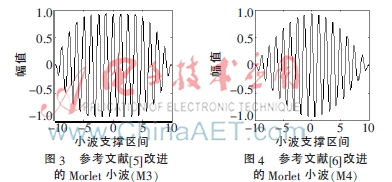
　　參考文獻[5]為了得到較好的檢測率,，提出了一種新的Morlet小波（波形如圖3所示）,，即：

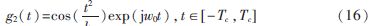
　　小波基函數(shù)的有效支撐區(qū)間為[-Tc，Tc],；由0≤t2/k≤π/2?圯k=2T2/π,。相比式（12）而言，式（16）通過增大N的值，把小波拉伸至類似余弦函數(shù)的其中一段,。從圖2和圖3可看出,，式（16）雖然有較好的幅頻特征，但卻使時域分辨率降低了,，所以它并沒有在整個時頻域內(nèi)使檢測概率以及檢測精度達到最佳效果,。因此，參考文獻[6]又對式（16）作了改進（波形如圖4所示）,。

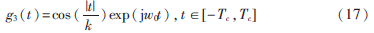
　　小波基函數(shù)的有效支撐區(qū)間為[-Tc,，Tc]，由0≤|t|/k≤π/2?圯k=2T/π,。從圖4可看出,，式（17）的性能優(yōu)于式（12）和式（14），因為它綜合考慮了時頻分辨率,。

　　通過分析可以發(fā)現(xiàn)Morlet小波的時域包絡隨著N的增大波形更趨近于一個二項式函數(shù),。但由于要綜合考慮時頻分辨率，而且被容許條件限制著,，N的值不可能無限增大,。依據(jù)上述分析，為達到較高的時頻分辨率及高檢測率,，提出了基于二項式函數(shù)的新的Morlet小波基函數(shù),，其表達式為：

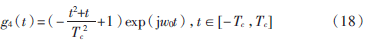
　　其中，w0為小波中心概率,；小波基函數(shù)的有效支撐區(qū)間為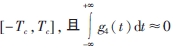,，近似滿足容許條件。設Tc=10時,，其波形如圖5所示,，各類小波基函數(shù)的幅頻特性如圖6所示。

　　從仿真圖可以看出,，M1小波雖然有較高的時域分辨率,，但是其頻域分辨率較差。M5既具有與M2幾乎同樣的衰減速度,，又具有像M3的時域窗口長度,、高檢測頻率和抗噪能力。相比較而言,，M5比M3和M4更滿足容許條件,，M5具有更好的時-頻分辨率和高檢測頻率。圖6描述的5類小波的幅頻特性中,，M1,、M2的幅值比M3,、M4和M5的小很多；M3的收斂速度比M4和M5的稍差,，雖然其幅值最大,；而M4和M5則具有同樣的收斂速度，但是綜合考慮時頻分辨率,，M5的幅值優(yōu)于M4,，因此M5的幅頻特征相對最優(yōu)。針對漸進信號,，用M5對應的小波基函數(shù)來提取信號小波脊線特征效果更佳,。

3 仿真結果與分析

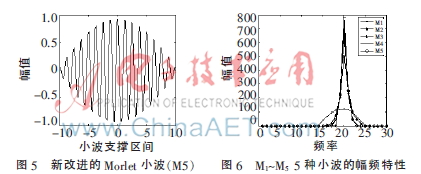
　　為驗證以上方法的有效性，下面利用上述的5種小波對BPSK和QPSK在信噪比為20 dB的情況下進行小波脊線特征的提取,，本文利用的是迭代算法提取小波脊線,，即參考文獻[7]的算法。信號參數(shù)設置如下：載頻20 MHz,，采樣頻率80 MHz,，編碼為7位Barker碼，脈寬為10 μs,。仿真結果如圖7~圖11所示,。

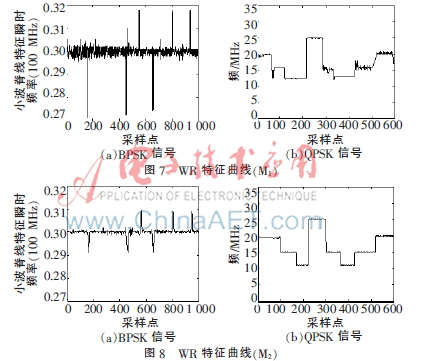
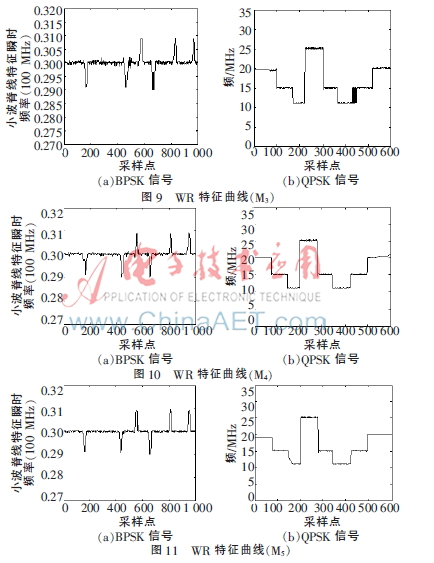
　　從圖7~11可以看出，在噪聲環(huán)境中,，M1的小波脊線特征提取的精確度明顯沒有其他幾個小波脊線的精確度高,，M1抗噪性能較差，易受噪聲影響,。在某些點上,，M2、M3,、M4的提取精確度沒有M5的高,。所以綜合看來，M5的提取效果比M2,、M3,、M4的提取效果好，抗噪聲能力比較強,。從上述仿真結果圖可以看出,，M5的小波脊線特征提取具有更優(yōu)良的抑制噪聲的能力，能更加準確地估計出信號的瞬時頻率,。

4 結論

　　本文在原有的Morlet小波基函數(shù)的基礎上,，通過改良提出了一個新的Morlet小波基函數(shù)，用于小波脊線特征的提取,，來更加準確地估計出雷達信號的瞬時頻率,，其理論性和實用性良好。MATLAB仿真結果顯示,，使用改良版Morlet小波提取出來的雷達信號的脊線特征能更好地抑制噪聲的影響,，檢測概率也有所提高，能更精確地為雷達信號的分選和識別提供依據(jù),。

參考文獻

　　[1] DELPART N. Asymptotic wavelet and Gabor analysis extraction of instantaneous frequencies[J]. IEEE Transactions on Information Theory,，1992，38（3）：644-664.

　　[2] MALLAT S. A wavelet tour of signal processing[M].San Diego,， CA： Academic Press,，1998.

　　[3] 余志斌，金煒東,，陳春霞.基于小波脊頻級聯(lián)特征的雷達輻射源信號識別[J].西南交通大學學報,，2010，45（2）：290-295.

　　[4] HO K C,， PROKOPIW W,， CHAN Y T. Modulation identification of digital signals by the wavelet[J]. Transform IEEE Proc-radar naving， 2000,，147（4）：169-176.

　　[5] 任春輝,，魏平，肖先賜.改進的Morlet小波在信號特征提取中的應用[J].電波科學報,，2003,，6（18）：633-637.

　　[6] 余志斌，陳春霞,，金煒東.一種新的Morlet小波及其在雷達信號特征提取中的應用研究[J].電路與系統(tǒng)學報,，2010，15（1）：129-134

　　[7] 王兵,，羿旭明.一種提取小波脊線的迭代算法[J].數(shù)學雜志,，2005，25（3）：295-298.

　　[8] 潘繼飛,，姜秋喜.一種脈間滑變雷達信號特征提取新方法[J].電子信息對抗技術,，2011（1）：80-99.

　　[9] 白航，趙擁軍,，趙國慶,，等.一種改進的雷達信號小波包特征提取方法[J].信息工程大學學報，2012（1）：12-14.