摘  要： 矩陣對(duì)策常用于解決對(duì)抗性決策問(wèn)題,，當(dāng)問(wèn)題復(fù)雜時(shí)人工求解困難,。為此，借助計(jì)算機(jī)的信息處理能力,，設(shè)計(jì)出具有可視化功能的矩陣對(duì)策專用軟件,，分析了矩陣對(duì)策的數(shù)學(xué)模型，給出了系統(tǒng)算法流程和對(duì)偶單純形法算法的計(jì)算步驟,，采用Qt圖形視圖框架,，借助C++ Boost數(shù)值計(jì)算庫(kù)ublas語(yǔ)言以及QtMmlWidget組件開發(fā)出矩陣對(duì)策專用軟件，以方便決策雙方快速合理地采取策略,。運(yùn)行算例表明,，該軟件操作方便，能夠公式化地顯示完整的計(jì)算過(guò)程,，具有跨平臺(tái)特性,。

　　關(guān)鍵詞： 矩陣對(duì)策；對(duì)偶單純形法,；Qt圖形視圖框架,；Boost

0 引言

　　矩陣對(duì)策又稱為二人有限零和對(duì)策，現(xiàn)已得到廣泛研究,，在體育比賽和政治經(jīng)濟(jì)談判等對(duì)抗性決策問(wèn)題應(yīng)用中取得了很大成就[1-2],，為制定最有利的行動(dòng)方案提供了理論依據(jù),。

　　國(guó)內(nèi)外已經(jīng)開發(fā)出多種計(jì)算矩陣對(duì)策的數(shù)學(xué)工具軟件，有MATLAB[3],、Lingo[4]與Mathematic[5]等,，雖然這類軟件功能強(qiáng)大，但比較復(fù)雜,，求解矩陣對(duì)策問(wèn)題前需要先建立數(shù)學(xué)模型,，再將原問(wèn)題轉(zhuǎn)化為線性規(guī)劃問(wèn)題。參考文獻(xiàn)[6]開發(fā)出用于解決矩陣對(duì)策問(wèn)題的程序Matrix Game Solver,，輸入贏得矩陣,，即可計(jì)算出對(duì)策值、局中人Ⅰ和Ⅱ的最優(yōu)決策向量,，但不能輸出計(jì)算過(guò)程,。參考文獻(xiàn)[7]設(shè)計(jì)了用于教學(xué)的矩陣對(duì)策程序，擁有良好的人機(jī)交互界面,，可以給出計(jì)算過(guò)程,，但操作步驟不夠靈活。

　　本文借助Qt圖形界面框架,、C++ Boost數(shù)值計(jì)算庫(kù),，通過(guò)QtMmlWidget組件解析數(shù)學(xué)標(biāo)記語(yǔ)言MathML，以實(shí)現(xiàn)對(duì)數(shù)學(xué)公式的渲染,，設(shè)計(jì)開發(fā)一款矩陣對(duì)策專用軟件系統(tǒng),，方便決策雙方快速采取合理的方案，同時(shí)使其具有跨平臺(tái)特性,，操作簡(jiǎn)單且能夠公式化地顯示完整的計(jì)算過(guò)程,。

1 矩陣對(duì)策數(shù)學(xué)模型及求解

　　記矩陣對(duì)策兩個(gè)局中人為Ⅰ、Ⅱ,，策略集S1,、S2如式（1）和式（2）所示，式（3）為矩陣對(duì)策的贏得矩陣A,。Ⅰ和Ⅱ分別有m和n個(gè)行動(dòng)策略,。

　　當(dāng)矩陣A存在鞍點(diǎn)時(shí)，其為純策略矩陣對(duì)策,，根據(jù)式（4）計(jì)算出純策略下的對(duì)策值及Ⅰ與Ⅱ的最優(yōu)純策略；反之,，A為混合策略矩陣對(duì)策,，求解時(shí)先分解出兩個(gè)互為對(duì)偶的線性規(guī)劃問(wèn)題，再采用對(duì)偶單純形法求解出混合策略下的對(duì)策值及Ⅰ與Ⅱ的最優(yōu)純策略[8],。

2 軟件結(jié)構(gòu)設(shè)計(jì)

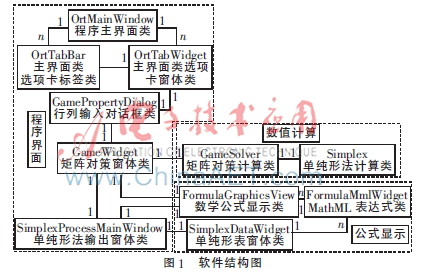
　　根據(jù)矩陣對(duì)策專用軟件使用簡(jiǎn)單,、操作方便的功能需求,，以及各模塊間相互獨(dú)立的設(shè)計(jì)思想，將軟件分為程序界面,、數(shù)值計(jì)算和結(jié)果,、計(jì)算過(guò)程顯示3個(gè)模塊。軟件結(jié)構(gòu)如圖1所示,，給出了各模塊包含的類以及模塊之間的關(guān)系,，通過(guò)Qt庫(kù)提供的信號(hào)與槽事件機(jī)制可以快速有效地實(shí)現(xiàn)各個(gè)模塊之間的消息傳遞與事件處理。

3 系統(tǒng)實(shí)現(xiàn)

　　3.1 系統(tǒng)設(shè)計(jì)平臺(tái)

　　Qt是一種跨平臺(tái)C++圖形用戶界面應(yīng)用程序開發(fā)框架,，具有良好的封裝機(jī)制,，在保證較高模塊化程度的同時(shí)也維系了很好的擴(kuò)展性，且其豐富的API為該矩陣對(duì)策軟件開發(fā)提供了很大的便利[9],。

　　Boost是一個(gè)可移植,、開放源代碼的C++準(zhǔn)標(biāo)準(zhǔn)庫(kù)，相當(dāng)于C++標(biāo)準(zhǔn)模板庫(kù)STL的擴(kuò)充,。對(duì)比STL,，Boost包含了更多工具類，更加實(shí)用,。

　　QtMmlWidget屬于Qt Solutions組件,，支持MathML2.0語(yǔ)言，以Unicode字體渲染各種數(shù)學(xué)符號(hào),，能夠直接將用MathML2.0語(yǔ)言編寫的數(shù)學(xué)公式對(duì)象移植到Qt程序中,。

　　該專用計(jì)算軟件以Qt框架提供的窗體、菜單等控件設(shè)計(jì)輸入輸出界面,；以C++為編程語(yǔ)言,，使用Boost數(shù)值計(jì)算庫(kù)ublas完成矩陣對(duì)策問(wèn)題的數(shù)值計(jì)算；最后提出公式的描述規(guī)則,，借助QtMmlWidget解析MathML,，實(shí)現(xiàn)對(duì)數(shù)學(xué)公式的渲染。

　　3.2 程序界面模塊

　　程序界面包括主界面,、贏得矩陣行列,、輸入輸出窗口、矩陣對(duì)策窗體及結(jié)果顯示界面,，為整個(gè)軟件系統(tǒng)提供與用戶間的交互功能,。程序主界面類與選項(xiàng)卡類間為一對(duì)多的關(guān)系，OrtTabWidget與行列輸入對(duì)話框類為一對(duì)一的關(guān)系,。因此,，系統(tǒng)可以接收多個(gè)行列數(shù)據(jù)的輸入，同時(shí)求解多個(gè)矩陣對(duì)策問(wèn)題,。

　　系統(tǒng)采用表格形式接收輸入的贏得矩陣數(shù)據(jù),，輸出分為純策略與混合策略兩種情況,，再用數(shù)學(xué)公式顯示類將結(jié)果顯示在矩陣對(duì)策窗體類中。純策略下贏得矩陣的解直接根據(jù)式（4）分析矩陣中各元素的值得到,，過(guò)程簡(jiǎn)單,，不生成中間數(shù)據(jù)?；旌喜呗韵孪到y(tǒng)給出單純形法輸出窗體,，包括兩個(gè)選項(xiàng)卡：線性規(guī)劃數(shù)學(xué)模型及其標(biāo)準(zhǔn)型和計(jì)算結(jié)果選項(xiàng)卡、迭代計(jì)算生成的單純形數(shù)據(jù)表顯示選項(xiàng)卡,。

　　3.3 數(shù)值計(jì)算模塊

　　數(shù)值計(jì)算模塊實(shí)現(xiàn)矩陣對(duì)策求解功能,。根據(jù)贏得矩陣是否存在鞍點(diǎn)設(shè)計(jì)算法流程如圖2所示，對(duì)偶單純形法求解混合策略下矩陣對(duì)策問(wèn)題的算法步驟如圖3所示,。當(dāng)贏得矩陣中存在負(fù)數(shù)時(shí),，將各元素減去最小負(fù)數(shù)，使矩陣中全部元素值非負(fù),。

　　3.4 結(jié)果及計(jì)算過(guò)程顯示模塊

　　根據(jù)MathML2.0的語(yǔ)法規(guī)則,，將數(shù)學(xué)公式分為單節(jié)點(diǎn)元素公式與多層嵌套節(jié)點(diǎn)樹公式。前者為數(shù)字,、運(yùn)算符等簡(jiǎn)單公式,，后者為矩陣、上下標(biāo)等復(fù)雜公式,。定義如下描述數(shù)學(xué)公式的語(yǔ)法規(guī)則：

　?。?）單節(jié)點(diǎn)元素公式

　　#mx（attr，value,，attr,，value，…）[data]#

　　式中,，mx只能為標(biāo)識(shí)符,、運(yùn)算符、數(shù)字,、文本之一,，data為公式的數(shù)據(jù)，attr和value為mx的屬性和值,。

　?。?）多層嵌套節(jié)點(diǎn)樹公式

　　#mx<level>（attr，value,，attr,，value，…）[data]&&mx<level>（attr，value,，attr，value,，…）[data]&&…#

　　其中,，各層公式標(biāo)記用&&隔開，level表示公式標(biāo)記的層數(shù),，從0開始逐層深入,，且第0層元素mx不能為標(biāo)識(shí)符、運(yùn)算符,、數(shù)字和文本,。

　　上述規(guī)則中，數(shù)學(xué)公式以成對(duì)的“#”出現(xiàn),。系統(tǒng)將計(jì)算數(shù)據(jù)按語(yǔ)法規(guī)則描述為字符串形式,，再傳遞給FormulaMmlWidget類。該類借助Qt庫(kù)中與XML相關(guān)類與函數(shù)將傳入的字符串轉(zhuǎn)換為符合MathML2.0標(biāo)準(zhǔn)的XML語(yǔ)句,，并以字符串的方式傳遞給父類QtMmlWidget進(jìn)行渲染[10],。實(shí)現(xiàn)數(shù)學(xué)公式顯示的步驟如圖4所示。

　　由于QtMmlWidget對(duì)MathML2.0支持并非十分完美,，在處理不等式對(duì)齊時(shí),，采用MathML呈現(xiàn)型標(biāo)記mphantom處理行與列的對(duì)齊問(wèn)題。經(jīng)渲染后的公式以Qt窗體元件顯示在數(shù)學(xué)公式顯示類與單純形表窗體類控件中,，前者可以顯示矩陣對(duì)策的解,、矩陣、線性規(guī)劃數(shù)學(xué)模型及其標(biāo)準(zhǔn)型,，后者用于顯示迭代過(guò)程中生成的單純形數(shù)據(jù)表格,。

4 應(yīng)用實(shí)例

　　設(shè)式（5）為待計(jì)算的矩陣對(duì)策問(wèn)題的贏得矩陣，輸入該矩陣后點(diǎn)擊“計(jì)算”按鈕,，運(yùn)行界面如圖5所示,。

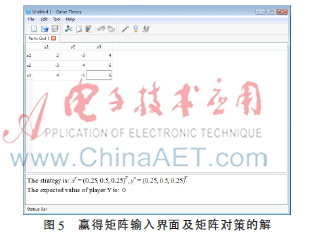
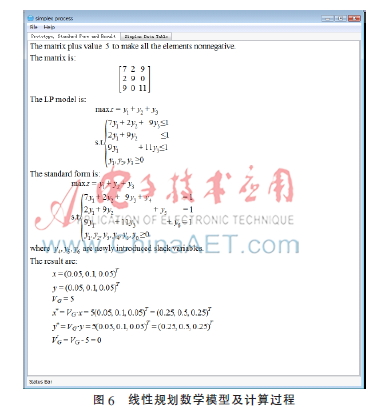
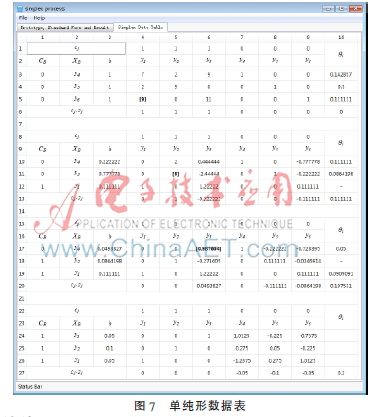
　　從圖5可以讀到局中人Ⅰ與Ⅱ最優(yōu)混合策略分別為（0.25，0.5,，0.25）T與（0.25,，0.5，0.25）T,，且局中人Ⅱ的期望值為0,。點(diǎn)擊“顯示”按鈕，得到圖6與圖7所示的對(duì)偶單純形法求解過(guò)程與中間數(shù)據(jù),。從圖6可以看出,，將輸入的矩陣各元素加5，使其全部非負(fù)。圖7顯示了經(jīng)過(guò)4次迭代計(jì)算求出問(wèn)題的最優(yōu)解,，單純形表中用“[]”標(biāo)記的粗體數(shù)字即為主元素,。整個(gè)計(jì)算過(guò)程可以公式化地顯示在界面中，清晰直觀,。

5 結(jié)論

　　本文論述了矩陣對(duì)策專用軟件系統(tǒng)的圖形化界面設(shè)計(jì)方法,，分析了純策略下與混合策略下矩陣對(duì)策問(wèn)題的模型及其求解方法，給出了數(shù)學(xué)公式的描述規(guī)則,，實(shí)現(xiàn)了文本,、矩陣等數(shù)學(xué)公式的顯示。從計(jì)算實(shí)例可以看出,，軟件使用簡(jiǎn)單,，操作方便，輸出直觀,，能夠快速方便地求解出任意的矩陣對(duì)策問(wèn)題,。在此軟件的基礎(chǔ)上，可以加入整數(shù)規(guī)劃等優(yōu)化問(wèn)題的分析計(jì)算模塊,，從而實(shí)現(xiàn)功能更豐富的運(yùn)籌學(xué)優(yōu)化軟件,。

　　參考文獻(xiàn)

　　[1] 楊靛青，李登峰．多目標(biāo)直覺模糊集矩陣對(duì)策的求解方法[J]．福州大學(xué)學(xué)報(bào)（自然科學(xué)版）,，2014,，42（2）：213-218．

　　[2] Li Dengfeng． Mathematical-programming approach to matrix games with payoffs represented by atanassov′s interval-valued intuitionistic fuzzy sets[J]． IEEE Transactions on Fuzzy Systems，2010,，18（6）：1112-1128．

　　[3] 陳杰．MATLAB寶典（第三版）[M]．北京：電子工業(yè)出版社,，2011．

　　[4] 謝金星，薛毅．優(yōu)化建模與LINDO/LINGO軟件[M]．北京：清華大學(xué)出版社,，2005．

　　[5] 陽(yáng)明盛,，林建華．Mathematica基礎(chǔ)及數(shù)學(xué)軟件[M]（第2版）．大連：大連理工大學(xué)出版社，2005．

　　[6] THOMAS S,， FERGUSON． Matrix game solver[EB/OL]．[2014-03-14].（2015-01-10）. http：//www.math.ucla.edu/~tom/gamesolve.html．

　　[7] 劉建永．運(yùn)籌學(xué)算法與編程實(shí)踐——Delphi實(shí)現(xiàn)[M]．北京：清華大學(xué)出版社,，2004．

　　[8] 《運(yùn)籌學(xué)》教材編寫組．運(yùn)籌學(xué)（第4版）[M]．北京：清華大學(xué)出版社，2012．

　　[9] 李文帆,，劉志剛,，伍文城，等．基于Qt的電力系統(tǒng)地理接線圖繪制軟件設(shè)計(jì)[J]．電力系統(tǒng)自動(dòng)化,，2013,，37（7）：72-76．

　　[10] 張光渝，楊秋輝,，詹聰,，等．開放式XML數(shù)據(jù)的質(zhì)量分析方法[J]．計(jì)算機(jī)應(yīng)用研究,，2013，30（7）：2082-2086．