摘  要： LLC變換器是一種非常有前景的拓?fù)潆娐?，然而其工作過程較為復(fù)雜，很難建立準(zhǔn)確的小信號模型,，因此閉環(huán)控制電路設(shè)計困難,。同時，隨著LLC變換器的廣泛使用,，其過流保護(hù)問題也日益受到關(guān)注,。針對一種具有過流保護(hù)功能的改進(jìn)型半橋LLC變換器，提出了基于Saber軟件時域仿真進(jìn)行補(bǔ)償電路設(shè)計的方法,，并設(shè)計了一款1 200 W的半橋型LLC變換器,。仿真實驗驗證了該方法的正確性及可行性,，對實際工程應(yīng)用有一定的指導(dǎo)意義。

　　關(guān)鍵詞： LLC變換器,；補(bǔ)償電路,；閉環(huán)控制；時域仿真

0 引言

　　LLC諧振式直流變換器由于可以實現(xiàn)原邊開關(guān)管的ZVS（Zero Voltage Switch）和副邊整流二極管的ZCS（Zero Current Switch）,，因而具有高效率,、高功率密度、低EMI噪聲等優(yōu)點(diǎn),，近年來受到了廣泛關(guān)注[1-2],。國內(nèi)外學(xué)者已對其拓?fù)浣Y(jié)構(gòu)[3]、諧振網(wǎng)絡(luò)參數(shù)優(yōu)化設(shè)計[4-5],、控制策略[6-7],、磁集成[8]等方面進(jìn)行了深入研究。為了獲得良好的穩(wěn)態(tài)指標(biāo)和動態(tài)指標(biāo),，在設(shè)計開關(guān)變換器時,，通常需要引入反饋控制環(huán)節(jié),。然而由于LLC變換器是一種強(qiáng)非線性系統(tǒng),，其工作過程非常復(fù)雜，很難建立精確的小信號模型[9-10],。同時,，隨著LLC變換器的廣泛使用,，其過流保護(hù)問題也日益受到關(guān)注[11-12]?；诖?，本文針對一種具有自限流功能的改進(jìn)型半橋LLC變換器[12]，提出了利用Saber仿真輔助設(shè)計閉環(huán)反饋控制電路的方法,，并設(shè)計了一款400 V輸入,、48 V輸出的半橋型LLC變換器進(jìn)行驗證。

1 改進(jìn)的半橋型LLC變換器的原理

　　LLC變換器在實際應(yīng)用中存在一些問題,，其中一個主要問題是當(dāng)電路啟動,、負(fù)載過重或短路時，如何有效抑制原邊諧振電流過沖,。圖1為一種有主動限流功能的改進(jìn)型半橋LLC變換器拓?fù)浣Y(jié)構(gòu)圖,。兩個主開關(guān)Q1和Q2共同構(gòu)成半橋結(jié)構(gòu)，以50%的占空比互補(bǔ)導(dǎo)通（包含死區(qū)時間）,。相對于傳統(tǒng)的半橋型LLC變換器,，改進(jìn)型仍然由諧振電感Lr、諧振電容Cr、勵磁電感Lm構(gòu)成諧振網(wǎng)絡(luò),，只是將諧振電容Cr分成了Cr1,、Cr2兩部分且并接上鉗位二極管。這樣設(shè)計會帶來兩方面的好處：（1）拆分的諧振電容會減小輸入電流紋波,，使諧振電流波形接近正弦,，減小EMI噪聲；（2）并聯(lián)的二極管在過載時會主動鉗位,，限制諧振電容兩端的電壓,，從而諧振電流也被鉗位，防止電路損壞,。

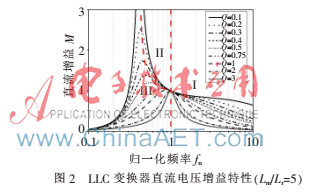
　　應(yīng)用基波分析法（FHA）對半橋型LLC變換器進(jìn)行穩(wěn)態(tài)分析,，得到其直流電壓增益特性曲線圖（如圖2所示），可將其工作狀況分為3個區(qū)域：Ⅰ區(qū)LLC電路工作在感性狀態(tài),，原邊開關(guān)管能夠?qū)崿F(xiàn)ZVS,，而副邊整流二極管電流連續(xù)，不能自然過零,，硬關(guān)斷,；Ⅱ區(qū)LLC電路工作在感性狀態(tài)，原邊開關(guān)管能實現(xiàn)ZVS,，且副邊整流二極管電流斷續(xù),，可自然過零，能夠?qū)崿F(xiàn)ZCS,，是LLC電路最理想的工作區(qū)域,；Ⅲ區(qū)諧振電路工作在容性狀態(tài)，電流超前電壓的變化,，可實現(xiàn)ZCS，是LLC電路不宜工作的區(qū)域,。由圖2可知在Ⅰ區(qū)和Ⅱ區(qū),，變換器的直流電壓增益為單調(diào)遞減函數(shù)，只要調(diào)整LLC變換器的開關(guān)頻率,，即可改變直流輸出電壓的大小,，所以通過引入反饋，控制開關(guān)頻率,，可達(dá)到穩(wěn)定輸出的目的,。

2 基于Saber時域仿真的小信號模型分析

　　由以上分析可知，LLC變換器是一種變頻調(diào)制變換器,，要想對LLC變換器進(jìn)行閉環(huán)補(bǔ)償電路設(shè)計,，必須獲得原邊開關(guān)頻率fs到輸出端電壓Vo的小信號傳遞函數(shù)，即,。然而,，到目前為止,，現(xiàn)有文獻(xiàn)還未給出該傳遞函數(shù)的準(zhǔn)確模型，這也直接導(dǎo)致了LLC反饋控制回路設(shè)計的困難,。

　　鑒于此,，采用Saber軟件中的TDSA模塊（頻率響應(yīng)分析儀）對改進(jìn)的LLC變換器開環(huán)電路進(jìn)行小信號時域仿真分析，可直接獲得傳遞函數(shù)P（s）的波特圖,。TDSA模塊（如圖3中右下角儀器）的output端子向待測電路中注入頻率可調(diào)的正弦信號,，input端子接入待測電路的輸出端作為反饋信號，通過比較兩端子的信號可以獲得兩者的增益和相位關(guān)系,，即波特圖,。同時，采用Saber中的VCO模塊（壓控振蕩器）來實現(xiàn)電路的變頻控制,。

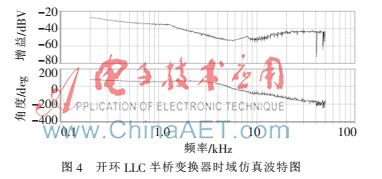
　　圖4所示為改進(jìn)的LLC變換器在400 V輸入,、48 V輸出、開關(guān)頻率100 kHz,、工作于Ⅱ區(qū)的情況下,，控制量開關(guān)頻率到輸出電壓的波特圖。由波特圖可知,，由于原邊開關(guān)頻率fs與輸出端電壓Vo的變化方向相反,，相頻曲線起始點(diǎn)位于100°附近。當(dāng)LLC變換器的開關(guān)頻率增大時,，變換器的輸出電壓會隨之變小,。分析可知，LLC變換器開環(huán)電路是高階系統(tǒng),，其開環(huán)傳遞函數(shù)存在多個零極點(diǎn),。其中有一個零點(diǎn)由電容的ESR形成。通常在設(shè)計閉環(huán)補(bǔ)償電路時,，為了有較好的穩(wěn)態(tài)誤差和動態(tài)特性,，希望校正后的系統(tǒng)在低頻時有較大的幅頻特性且具有一定的相位裕度（45°~75°）。由于相頻曲線起始點(diǎn)位于100°附近,，使開環(huán)系統(tǒng)在較寬的頻率范圍內(nèi),，具有較大的相位超前特性，導(dǎo)致原系統(tǒng)的相位裕度過大,。原系統(tǒng)低頻段幅頻特性斜率為-10 dB/dec,，故希望有較大的增益，這樣可以獲得較好的動態(tài)特性,。原系統(tǒng)中頻段幅頻特性斜率為-40 dB/dec,，滿足要求，無需補(bǔ)償。在高頻段,，原系統(tǒng)的相頻特性有較大振蕩,，這給系統(tǒng)帶來了不穩(wěn)定的因素，因此希望校正后的系統(tǒng)在高頻環(huán)節(jié)能夠盡量下降得快些,，同時有利于抑制高頻開關(guān)噪聲,。

　　參考文獻(xiàn)[9]指出可以通過擴(kuò)展描述函數(shù)法對LLC變換器進(jìn)行小信號建模，獲得其系統(tǒng)開環(huán)傳遞函數(shù)的零極點(diǎn)分布,，并指出在區(qū)域Ⅰ有一個與輸出濾波電容,、負(fù)載和諧振電路參數(shù)有關(guān)的低頻極點(diǎn)，一雙重極點(diǎn)和一個與電容ESR有關(guān)的零點(diǎn),。當(dāng)開關(guān)頻率靠近諧振頻率時,，一個移向高頻處，一個向低頻極點(diǎn)靠近,。由于負(fù)載變動時,，閉環(huán)控制的LLC變換器會通過改變頻率調(diào)整電壓增益改變輸出，因此實際上此時LLC變換器也可能隨著負(fù)載的變動工作于Ⅰ區(qū),。綜合考慮,，在此選擇雙零點(diǎn)雙極點(diǎn)補(bǔ)償器（補(bǔ)償電路和波特圖如圖5所示），它結(jié)合超前補(bǔ)償與滯后補(bǔ)償?shù)奶匦?，發(fā)揮滯后補(bǔ)償特性提高靜態(tài)性能,，利用超前補(bǔ)償特性提高相對穩(wěn)定性和動態(tài)性能。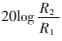雙零點(diǎn)雙極點(diǎn)補(bǔ)償電路對應(yīng)的傳遞函數(shù)如式（1）所示,，通過對轉(zhuǎn)折點(diǎn)頻率的設(shè)定,，可方便靈活地實現(xiàn)各頻率段的補(bǔ)償，通過改變的值,，可以使系統(tǒng)傳遞函數(shù)波特圖上下移動,，從而改變增益和相位的裕量。這樣,，即可方便地實現(xiàn)系統(tǒng)閉環(huán)補(bǔ)償電路的設(shè)計,。補(bǔ)償后的閉環(huán)系統(tǒng)波特圖如圖6所示。

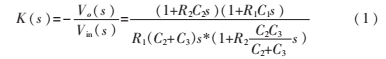
　　同時,，選擇雙零點(diǎn)雙極點(diǎn)補(bǔ)償電路還有一個優(yōu)點(diǎn),，即可很容易得到其Z域變換方程（如式（1）所示）,，并且可方便差分化,，易于在DSP系統(tǒng)編程實現(xiàn)，其相應(yīng)差分方程如式（3）所示,。

　　u（k）=b0e（k）+b1e（k-1）+b2e（k-2）-a1u（k-1）-a2u（k-2）（3）

3 仿真實驗驗證

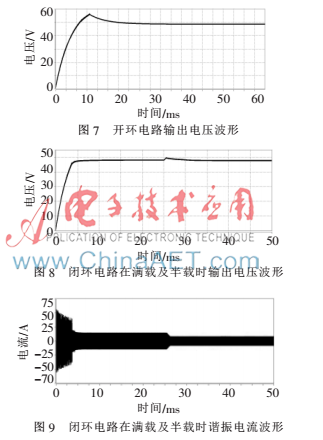
　　基于Saber軟件時域仿真,，在此設(shè)計一款額定工作頻率100 kHz，額定輸入400 V，額定輸出1 200 kW（48 V/25 A）的閉環(huán)半橋LLC變換器進(jìn)行實驗驗證,。電路參數(shù)：Lr=10 μH,，Lm=58 μH，Cr1=110 nF,，Cr2=110 nF,，濾波電容Co=4 000 μF，變壓器匝比2.5∶1,。圖7為其開環(huán)電路滿載時輸出電壓波形,，可以看出其超調(diào)量近20%。圖8為其閉環(huán)電路滿載和在0.025 s切換到半載時輸出電壓的波形,，圖9為此情況下相應(yīng)的諧振電流波形,。仿真實驗結(jié)果表明，在滿載和半載時所設(shè)計電路都能達(dá)到較好的穩(wěn)態(tài)和動態(tài)指標(biāo),，同時諧振電流波形未出現(xiàn)電流過沖的尖峰,，表明改進(jìn)的LLC拓?fù)潆娐吩陔娐穯訒r達(dá)到了主動限流的作用，保護(hù)了電路元件,。

4 結(jié)論

　　LLC諧振變換器工作過程復(fù)雜,，小信號建模比較困難，本文利用Saber對一種具有自限流功能的半橋LLC變換器進(jìn)行時域仿真,，得到簡化的小信號模型,，進(jìn)而實現(xiàn)閉環(huán)反饋補(bǔ)償電路的設(shè)計，仿真實驗結(jié)果驗證了該方法的正確性和可行性,。

參考文獻(xiàn)

　　[1] YANG B,， LEE F C， ZHANG A J,， et al. LLC resonant converter for front end DC/DC conversion[C]. Seventeerth Annual IEEE,， Applied Power Electronics Conference and Exposition， APEC 2002,， 2002,，2：1108-1112.

　　[2] Fu Dianbo， LEE F C,， Liu Ya,， et al. Novel multi-element resonant converters for front-end DC/DC converters[C]. Proceedings of IEEE Power Electronics Specialists Conference， PESC 2008,， 2008：250-256.

　　[3] Yang Bo. Topology investigation for front end DC/DC power conversion for distributed power system[D]. Virginia Polytechnic Institute and State University,， USA， 2003.

　　[4] STMicroelectronics. LLC resonant half-bridge converter design guideline[S]. 2009.

　　[5] Lu Bing,， Liu Wenduo,， Liang Yan,， et al. Optimal design methodology for LLC resonant converter[C]. Twenty-First Annual IEEE Applied Power Elecfronics Conference and Exposition， 2006,， APEC′06,， 2006：533-538.

　　[6] JU W C. LLC DC/DC resonant converter with PLL control scheme[D]. National Cheng Kung University， 2006.

　　[7] Hang Lijun,， Lu Zhengyu,， Qian Zhaoming. Research of digital control strategy for multi-resonant LLC converter[C]. IEEE International Symposium on Industrial Electronics， 2007：479-484.

　　[8] Yang Bo,， Chen Rengang,， LEE F C. Integrated magnetic for LLC resonant converter[C]. Seventkenth Annual IEEE Applied Power Electronics Conference and Exposition， APEC 2002,， 2002,， 2：346-351.

　　[9] YANG E X. Extended describing function method for small-signal modeling of resonant and multi-resonant converters[J]. Dissertation， Virginia Tech,， Black sburg,， VA， February 1994.

　　[10] LAZAR,， MARTINELLI R. Stedy-state analysis of the LLC series resonant converter[C]. Sixteenth Annual IEEE Applied Power Electronics Conference and Exposition,， APEC 2001， 2001,，2：728-735.

　　[11] Xie Xiaogao,， Zhang Junming， Zhao Chen,， et al. Analysis and optimization of LLC resonant converter with a novel over current protection circuit[J]. IEEE Transactions on Power Electronics,， 2007， 22：435-443.

　　[12] YANG B,， LEE F C,， CONCANNON M. Over current protection methods for LLC resonant converter[C]. Proceedings of 18th Annual IEEE Applied Power Electronics Conference and Exposition， 2003：605-609.