摘  要： 挖掘頻繁閉項(xiàng)集（CFI）在許多實(shí)際應(yīng)用中起著重要的作用,。傳統(tǒng)的數(shù)據(jù)挖掘算法中常用FP增長(zhǎng)算法和Apriori算法來(lái)挖掘頻繁項(xiàng)集,。然而，內(nèi)存需求和計(jì)算成本成為CFI挖掘算法的瓶頸,，尤其是在從大型數(shù)據(jù)集中挖掘頻繁閉項(xiàng)集時(shí),，是一個(gè)重要和具有挑戰(zhàn)性的問(wèn)題。針對(duì)上述問(wèn)題,，提出一種基于云計(jì)算的MapReduce框架的并行AFOPT-close算法,，使MapReduce可廣泛地用于處理大型數(shù)據(jù)。此外,，用于檢查頻繁項(xiàng)集是否為完全閉的有效并行算法也要求MapReduce平臺(tái)進(jìn)一步完善其性能,。

　　關(guān)鍵詞： MapReduce；頻繁閉項(xiàng)集,；FP增長(zhǎng)算法

0 引言

　　頻繁閉項(xiàng)集挖掘（Closed Frequent Itemset,，CFI）在1999年由Pasquier等人提出[1]。作為一種代替?zhèn)鹘y(tǒng)頻繁項(xiàng)集挖掘（Frequent Itemset Mining,，F(xiàn)IM）的新算法,，CFI挖掘的優(yōu)點(diǎn)在于在相同的頻繁項(xiàng)集挖掘效率下大大降低了冗余規(guī)則并且增加了挖掘的效率和有效性。自CFI出現(xiàn)以來(lái)一直被廣泛地研究,，現(xiàn)有的CFI挖掘算法可分為兩類(lèi)：候選項(xiàng)集生成和檢測(cè)方法[1]和模式增長(zhǎng)方式[2-4],。

　　這些算法在處理小數(shù)據(jù)集或者支持度閾值較高時(shí)有良好的性能，但是當(dāng)處理大數(shù)據(jù)集或者支持度閾值變小時(shí)內(nèi)存運(yùn)行開(kāi)銷(xiāo)將大幅度增加,。一些早期的工作重點(diǎn)在于使用PC集群運(yùn)行算法來(lái)加快挖掘速度,，這樣可以提高挖掘性能，但是也對(duì)諸如負(fù)載平衡,、數(shù)據(jù)分區(qū),、通信成本最小化、因通信節(jié)點(diǎn)失效引起的錯(cuò)誤等問(wèn)題提出了新的挑戰(zhàn)。

　　為了克服上述缺點(diǎn),，設(shè)計(jì)了MapReduce框架來(lái)支持云計(jì)算分布式計(jì)算的計(jì)算模式,，對(duì)于大型數(shù)據(jù)集而言這是一個(gè)進(jìn)行并行數(shù)據(jù)挖掘的有效平臺(tái)。為了能更好地利用MapReduce在CFI挖掘中的優(yōu)勢(shì),，本文基于MapReduce設(shè)計(jì)并實(shí)現(xiàn)了一個(gè)并行算法[4],，這種算法是一種類(lèi)似于FP增長(zhǎng)算法的分治算法，能夠有效地挖掘頻繁閉項(xiàng)集,。此外,，也提出了一種檢查一個(gè)頻繁項(xiàng)集是否是完全閉的有效并行化方法，該方法能夠過(guò)濾掉冗余的頻繁項(xiàng)集,。

1 頻繁項(xiàng)集挖掘改進(jìn)算法

　　在現(xiàn)有的研究中[3,，5]已經(jīng)設(shè)計(jì)出能夠在內(nèi)存共享情況下的多線(xiàn)程的FP增長(zhǎng)算法，但當(dāng)面臨大規(guī)模數(shù)據(jù)集時(shí)這些方法將遇到內(nèi)存需求嚴(yán)重不足的問(wèn)題,。一些研究工作也致力于解決更多細(xì)節(jié)問(wèn)題,，如通信開(kāi)銷(xiāo)最小化，內(nèi)存的利用率最大化等[6-8],。例如WHANG K Y等人提出了一種在無(wú)共享環(huán)境下FP增長(zhǎng)算法并行執(zhí)行的方法,，該算法可以實(shí)現(xiàn)良好的可擴(kuò)展性，但是也存在同樣的問(wèn)題,。隨著云計(jì)算的發(fā)展,，MapReduce平臺(tái)能夠?qū)Υ鎯?chǔ)在大型計(jì)算機(jī)集群上的龐大數(shù)據(jù)進(jìn)行分布式處理，具有良好的可擴(kuò)展性和魯棒容錯(cuò)性,。因此提出了許多基于MapReduce的頻繁項(xiàng)集挖掘改進(jìn)算法,。例如李浩源等人基于MapReduce提出了一種并行的FP增長(zhǎng)算法PFP[9]，該算法將整個(gè)挖掘任務(wù)分割成若干獨(dú)立的并行子任務(wù),，并實(shí)現(xiàn)了擬線(xiàn)性加速比。除了可擴(kuò)展性,，PFP還讓設(shè)計(jì)基于MapReduce的模式增長(zhǎng)方式成為可能,。在以前的研究中，也有對(duì)基于MapReduce的閉頻繁項(xiàng)集算法的相關(guān)討論和實(shí)現(xiàn)[10],，主要通過(guò)以下4個(gè)步驟來(lái)完成該算法,，其中3個(gè)步驟是MapReduce操作。

　?。?）并行計(jì)算,。統(tǒng)計(jì)數(shù)據(jù)庫(kù)中每個(gè)項(xiàng)目的支持度。

　?。?）構(gòu)建全局的F-List（鏈?zhǔn)綌?shù)據(jù)結(jié)構(gòu)）,。把項(xiàng)目按出現(xiàn)頻率遞減的順序分類(lèi)并排除支持度小于最小支持度閾值的項(xiàng)目（用ξ表示）。

　?。?）并行挖掘頻繁閉項(xiàng)集,。并行挖掘局部頻繁閉項(xiàng)集,。

　　（4）并行過(guò)濾冗余項(xiàng)集,。過(guò)濾局部閉而非全局閉的頻繁項(xiàng)集,。

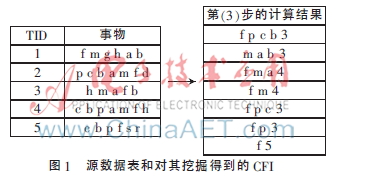
　　通過(guò)上面4個(gè)步驟，能夠準(zhǔn)確地挖掘頻繁閉項(xiàng)集,。如圖1中的一個(gè)簡(jiǎn)單例子,，左邊部分是原始事務(wù)表，右邊部分給出通過(guò)步驟（1）~（4）挖掘得到的CFI,，其中ξ=3,。右邊部分每個(gè)項(xiàng)集的最后一項(xiàng)為支持度閾值。顯然,，這存在一些局部閉而非全局閉的冗余項(xiàng)集,，例如{f m 4}，{f p c 3},，{f p 3},。

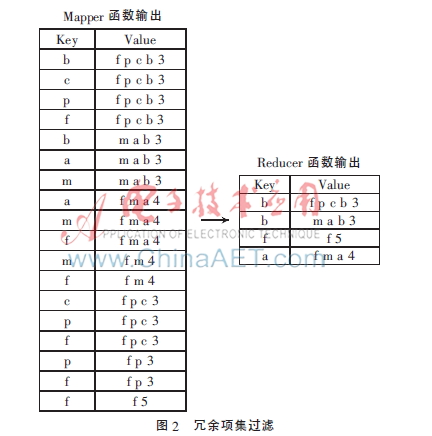
　　在第（4）步中使用了并行的方法來(lái)過(guò)濾冗余項(xiàng)集。如圖2所示,，首先,，每個(gè)mapper函數(shù)從CFI中讀入一個(gè)項(xiàng)集，然后輸出n次,，n為項(xiàng)集的長(zhǎng)度,，Key為在項(xiàng)集中出現(xiàn)的項(xiàng)目。然后,，每個(gè)reducer函數(shù)接收相應(yīng)的值并且將項(xiàng)集按他們的長(zhǎng)度遞減分類(lèi),，這樣做是為了避免超集的檢測(cè)，接下來(lái)并行地過(guò)濾冗余項(xiàng)集,。最后,，該項(xiàng)集的Key為最終保存的項(xiàng)。這種方法雖然可行,，但是也導(dǎo)致了嚴(yán)重的通信開(kāi)銷(xiāo)和計(jì)算成本,。以頻繁項(xiàng)集{f p c b 3}為例，3為該項(xiàng)集的支持度閾值,。該方法需要發(fā)送這個(gè)項(xiàng)集4次：分別是{f：f p c b 3},、{p：f p c b 3}、{ c：f p c b 3},、{ b：f p c b 3},。顯然，這4個(gè)項(xiàng)集將會(huì)按不同的Key值被發(fā)送到reducer函數(shù)4次。如果ξ足夠小,，將可能有許多很長(zhǎng)的頻繁項(xiàng)集被反復(fù)地發(fā)送到reducer函數(shù),。因此，這種方法的總體開(kāi)銷(xiāo)會(huì)非常高,。為了解決這個(gè)問(wèn)題,，本文提出了一種高效的并行CFI挖掘算法，該算法也采用了一種新穎的冗余項(xiàng)集過(guò)濾方法來(lái)降低通信開(kāi)銷(xiāo)和計(jì)算成本,。

2 并行AFOPT-close算法

　　2.1 算法的定義

　　在本節(jié)中,，提出了一種有效的冗余項(xiàng)集過(guò)濾方法，即并行AFOPT-close算法,。如上所述,，直接基于MapReduce采用并行化的方法挖掘頻繁閉項(xiàng)集會(huì)導(dǎo)致一些項(xiàng)集可能局部閉而非全局閉的問(wèn)題。在本節(jié)中,，將對(duì)局部頻繁閉項(xiàng)集和全局頻繁閉項(xiàng)集分別進(jìn)行定義,。

　　定義1 局部頻繁閉項(xiàng)集

　　如果頻繁項(xiàng)集X在步驟（3）中的reducer中是閉的，那么頻繁項(xiàng)集X為局部頻繁閉項(xiàng)集,，用L表示局部項(xiàng)集,。

　　定義2 全局頻繁閉項(xiàng)集

　　如果頻繁項(xiàng)集X對(duì)于所有局部頻繁閉項(xiàng)集都是閉的，那么頻繁項(xiàng)集X為全局頻繁閉項(xiàng)集,。用G表示全局項(xiàng)集,。

　　性質(zhì)：假設(shè)存在X∈L，如果X對(duì)于所有的項(xiàng)集{Y|Y∈L and supp（X）=supp（Y）}都是閉的,，那么X∈G,。

　　定義3 冗余項(xiàng)集

　　當(dāng)且僅當(dāng)頻繁項(xiàng)集X∈L且X?埸G，那么頻繁項(xiàng)集X為冗余項(xiàng)集,，用R表示冗余,。

　　2.2 高效冗余項(xiàng)集過(guò)濾

　　在現(xiàn)有的研究中，提出了一種基本方法來(lái)過(guò)濾冗余項(xiàng)集,，該方法因計(jì)算成本和通信開(kāi)銷(xiāo)太高而很費(fèi)時(shí),。本文基于2.1節(jié)中的定義提出了一種新的方法來(lái)解決這個(gè)問(wèn)題。當(dāng)然,，可以通過(guò)選出具有相同支持度的全局閉頻繁項(xiàng)集而輕松地實(shí)現(xiàn)一個(gè)高效冗余過(guò)濾算法。因此,，把一個(gè)項(xiàng)集的支持度作為一個(gè)項(xiàng)集的關(guān)鍵,，具有相同支持度的項(xiàng)集會(huì)被發(fā)送到同一個(gè)reducer函數(shù)。將在下面的算法1中給出這種方法的簡(jiǎn)要代碼,，該方法的開(kāi)始3步與參考文獻(xiàn)[10]中提出的算法描述的一樣（Suppose X∈L）,。

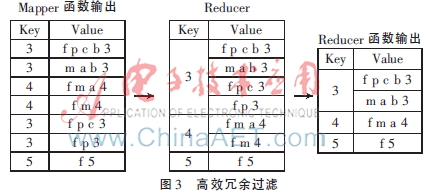
　　算法1的處理過(guò)程如下：首先，每個(gè)mapper函數(shù)一行一行地從第（3）步中讀取輸出結(jié)果并且輸出<key，value>對(duì)和<supp（X）,，X>,。這樣，具有相同支持度的項(xiàng)集會(huì)被發(fā)送到相同的reducer函數(shù)中并壓縮成一棵樹(shù),。然后,，冗余項(xiàng)集會(huì)被并行地過(guò)濾掉。如圖1所示,，只需要把每個(gè)項(xiàng)集發(fā)送到局部頻繁閉項(xiàng)集中一次（如圖1的左半部分）,，而已有的方法[10]需要發(fā)送每個(gè)項(xiàng)集至少3次，如圖3所示,。對(duì)于具有n個(gè)項(xiàng)集的數(shù)據(jù)庫(kù),，每個(gè)項(xiàng)集的長(zhǎng)度是{m1，m2,，…,，mn}。在傳統(tǒng)方法[10]中,，項(xiàng)集需要發(fā)送m1+m2+…+mn次,，也就是說(shuō)，該方法約節(jié)約了（m1+m2+…+mn）/n（即項(xiàng)集的平均長(zhǎng)度）倍的通信成本,。

　　算法1 高效冗余項(xiàng)集過(guò)濾

　　Procedure：Map（key,，value=supp（X）+X）

　　for each value do

　　output（supp（X），X）,；

　　end for

　　end Procedure

　　Procedure：Reduce（key,，Iterable values）

　　Define and initialize a tree：r；

　　Sort the itemsets by their lengths in descending order,；

　　for each itemset in values do

　　if itemset is closed in r then

　　Insert the itemset into r,；

　　end if

　　end for

　　for each itemset in r do

　　output（key，itemset）,；

　　end for

　　end Procedure

3 性能仿真與結(jié)果分析

　　為了驗(yàn)證該方法的效率和有效性,，將在兩個(gè)下載的真實(shí)的數(shù)據(jù)庫(kù)connect和webdocs中做實(shí)驗(yàn)。實(shí)驗(yàn)在6臺(tái)裝有Hadoop0.21.0的計(jì)算機(jī)組成的計(jì)算機(jī)群上進(jìn)行,，計(jì)算機(jī)配置為Intel 4核處理器,，4 GB內(nèi)存和500 GB硬盤(pán)，裝有Ubuntu10.10,。其中一個(gè)節(jié)點(diǎn)被設(shè)為主節(jié)點(diǎn),，負(fù)責(zé)安排執(zhí)行不同節(jié)點(diǎn)之間的任務(wù)；其他節(jié)點(diǎn)負(fù)責(zé)運(yùn)行,。算法用Java實(shí)現(xiàn),，JDK版本為openjdk-6-jdk,。

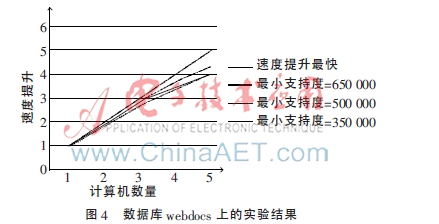
　　圖4顯示了在webdocs數(shù)據(jù)庫(kù)上實(shí)驗(yàn)的結(jié)果。當(dāng)ξ=650 000時(shí),，該算法擁有最大的斜率值,。因?yàn)楫?dāng)ξ越大，對(duì)于在第（3）步中的每個(gè)reducer函數(shù)而言,，本地?cái)?shù)據(jù)庫(kù)越小,，所以在第（3）步和第（4）步中耗費(fèi)的時(shí)間越短，而在第（1）步和第（2）步中消耗的時(shí)間依然保持不變,。

　　圖5顯示了在connect數(shù)據(jù)庫(kù)上實(shí)驗(yàn)的結(jié)果,。由于該數(shù)據(jù)庫(kù)比較小，速度上的提高不如圖4的明顯,。從圖5可以看出,，用4臺(tái)電腦比用5臺(tái)電腦更能提高速度。原因在于對(duì)于每個(gè)節(jié)點(diǎn)而言,，數(shù)據(jù)集太小,，導(dǎo)致通信成本遠(yuǎn)高于計(jì)算成本。實(shí)驗(yàn)結(jié)果表明,，該算法對(duì)于大規(guī)模的數(shù)據(jù)集擁有良好的可擴(kuò)展性,，對(duì)于小規(guī)模數(shù)據(jù)集則不然。

　　對(duì)上述新冗余過(guò)濾算法和傳統(tǒng)算法[10]在項(xiàng)集發(fā)送次數(shù)上作對(duì)比,，結(jié)果如表1所示,。例如數(shù)據(jù)集connect，如果不適用新的冗余過(guò)濾算法,，如果數(shù)據(jù)集過(guò)大勢(shì)必使計(jì)算成本和通信開(kāi)銷(xiāo)變得很高,。根據(jù)表1，顯然當(dāng)ξ=24 000時(shí),，傳統(tǒng)算法[10]與上述算法在項(xiàng)集發(fā)送次數(shù)的對(duì)比中可以看出新的冗余過(guò)濾算法的優(yōu)越性,。但是，該方法在webdocs數(shù)據(jù)庫(kù)上卻沒(méi)有明顯優(yōu)勢(shì),，原因在于在第（3）步中產(chǎn)生的項(xiàng)集的平均長(zhǎng)度過(guò)短,。由此可見(jiàn)，新算法對(duì)于長(zhǎng)項(xiàng)集而言比短項(xiàng)集具有更高的效率,。

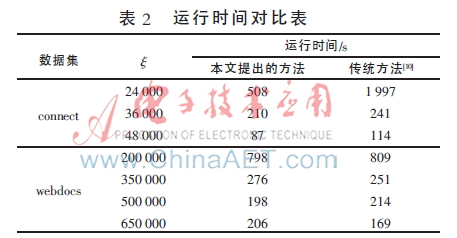
　　對(duì)上述算法與傳統(tǒng)算法[10]作運(yùn)行時(shí)間上的對(duì)比,，如表2所示。實(shí)驗(yàn)在5臺(tái)負(fù)責(zé)運(yùn)行的計(jì)算機(jī)組成的計(jì)算機(jī)群上進(jìn)行,，用兩個(gè)相同的數(shù)據(jù)集但是閾值不同,。從表2可以看出，由于局部閉頻繁項(xiàng)集比源數(shù)據(jù)集要大而且項(xiàng)集自身的平均長(zhǎng)度也很長(zhǎng),，因此上述算法對(duì)于connect數(shù)據(jù)庫(kù)而言更高效,。綜上所述，該算法的運(yùn)行速度更快,。但是對(duì)于webdocs,，當(dāng)ξ取350 000、500 000和650 000時(shí)該算法沒(méi)有優(yōu)勢(shì),，主要是由于第（3）步輸出的結(jié)果太小,。然而當(dāng)ξ=200 000時(shí)，該算法比傳統(tǒng)算法快得多,，這是因?yàn)榈冢?）步的輸出結(jié)果足夠大并且具有更多長(zhǎng)項(xiàng)集,。

4 結(jié)論

　　本文回顧了頻繁閉項(xiàng)集挖掘現(xiàn)存的問(wèn)題，并且提出了一種新的過(guò)濾局部閉而非全局閉頻繁項(xiàng)集的方法,。實(shí)驗(yàn)結(jié)果顯示,，該算法在面對(duì)大規(guī)模數(shù)據(jù)集時(shí)擁有很高的可擴(kuò)展性。當(dāng)局部閉頻繁項(xiàng)集很大,，尤其是對(duì)于一些閾值非常小或者項(xiàng)集過(guò)長(zhǎng)的挖掘中,，通信開(kāi)銷(xiāo)將嚴(yán)重影響算法性能。而本文所提方法能很好地解決這個(gè)問(wèn)題,。今后,，將繼續(xù)改進(jìn)該算法，使之有更高的效率和更廣的使用面,。

參考文獻(xiàn)

　　[1] 廖寶魁,，孫雋楓.基于MapReduce的增量數(shù)據(jù)挖掘研究[J].微型機(jī)與應(yīng)用，2014,，33（1）：67-70.

　　[2] Wang Jianyong,， Han Jiawei， Pei Jian. CLOSET+：searching for the best strategies for mining frequent closed itemsets[C]. Proceedings of the ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,， ACM,， 2003：236-245.

　　[3] FELDMAN R， DAGAN I. Knowledge discovery in textual databases（KDT）[C]. Proceedings of 1st International Conference on Knowledge Discovery and Data Mining,， Montreal,，Canada， 1995：112-117.

　　[4] ZANE O,， EL-HAJJ M,， LU P. Fast parallel association rule mining without candidacy generation[C]. Proceedings of IEEE International Conference on Data Mining， ICDM 2001,， 2001：665-668.

　　[5] Liu Li,， Li E， Zhang Yimin,， et al. Optimization of frequent itemset mining on multiple-core processor[C]. Proceedings of the 33rd International Conference on Very Large Data Bases,， VLDB Endowment,， 2007：1275-1285.

　　[6] MADRIA K， BHOWMICK S. Research issue in web data mining[C]. First International Proceedings of Data Warehousing and Knowledge Discovery,， 1999：303-312.

　　[7] PRAMUDIONO I,， KITSUREGAWA M. Parallel fp-growth on pc cluster[J]. Advances in Knowledge Discovery and Data Mining， 2003,， 2637：467-473.

　　[8] BUEHRER G,， PARTHASARATHY S， TATIKONDA S,， et al. Toward terabyte pattern mining： an architecture conscious solution[C]. Proceedings of the 12th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming,， ACM， 2007：2-12.

　　[9] 蔣翠清,，胡俊妍.基于FP-tree的最大頻繁項(xiàng)集挖掘算法[J].合肥工業(yè)大學(xué)學(xué)報(bào)（自然科學(xué)版）,，2010，33（9）：1387-1391.

　　[10] 陳光鵬,，楊育彬,，高陽(yáng)，等.一種基于MapReduce的頻繁閉項(xiàng)集挖掘算法[J].模式識(shí)別與人工智能,，2012,，25（2）：220-224.