摘  要： 對(duì)柔性流水車間調(diào)度問(wèn)題（FFSP）進(jìn)行了分析闡述，在此基礎(chǔ)上對(duì)某飼料廠的飼料生產(chǎn)過(guò)程建立了具有機(jī)器靈活性的柔性流水車間調(diào)度模型,，該模型中存在多臺(tái)制粒機(jī),，既能加工大顆粒飼料，又能加工小顆粒飼料,，但是必須在開始加工之前確定各臺(tái)機(jī)器的用途,，增加了柔性流水車間調(diào)度的難度。利用新型的粒子群算法以最小化最大完工時(shí)間為目標(biāo)對(duì)該模型求解,，為了克服粒子群算法易陷入局部極值的缺點(diǎn),，提出基于位置相似度的鄰域結(jié)構(gòu)，并對(duì)鄰域內(nèi)的較優(yōu)粒子采用基于最大完工時(shí)間排序的學(xué)習(xí)方式進(jìn)行局部搜索,。實(shí)驗(yàn)結(jié)果表明,，該方法有利于克服粒子群算法的早熟缺陷，有效地解決了飼料生產(chǎn)調(diào)度問(wèn)題,，有一定的應(yīng)用價(jià)值,。

　　關(guān)鍵詞： 柔性流水車間；機(jī)器靈活性,；飼料,；局部搜索；粒子群

0 引言

　　柔性流水車間調(diào)度問(wèn)題（Flexible Flowshop Scheduling Problem,，F(xiàn)FSP）是一種更加復(fù)雜也更貼近實(shí)際的流水線調(diào)度問(wèn)題,，屬于典型的NP難問(wèn)題。由于該問(wèn)題具有重要的學(xué)術(shù)價(jià)值和應(yīng)用價(jià)值,，在將近半個(gè)世紀(jì)的研究中已取得較大的進(jìn)展,。早期對(duì)柔性流水車間調(diào)度問(wèn)題的求解主要是利用精確算法[1]和啟發(fā)式方法[2],。精確算法在理論上可以得到調(diào)度問(wèn)題的最優(yōu)解，但是在求解時(shí)間上無(wú)法讓人接受,，一般只用來(lái)解決小規(guī)模問(wèn)題,。而啟發(fā)式方法能夠在較短時(shí)間內(nèi)給出解決方案，但是解的質(zhì)量無(wú)法保證,。近年來(lái)智能算法[3-6]得到廣泛青睞,，如模擬退火算法、禁忌搜索算法,、免疫算法、遺傳算法,、蟻群算法,、蜂群算法、粒子群算法等,。

　　本文對(duì)某飼料廠的飼料生產(chǎn)過(guò)程進(jìn)行調(diào)研以后,，發(fā)現(xiàn)目前的飼料行業(yè)普遍還采用人工調(diào)度，調(diào)度計(jì)劃的優(yōu)劣完全取決于調(diào)度人員的經(jīng)驗(yàn),。而飼料生產(chǎn)過(guò)程可抽象為柔性流水線,，于是本文建立了一種帶機(jī)器靈活性的柔性流水車間調(diào)度模型，利用智能算法——粒子群優(yōu)化（Partical Swarm Optimization,，PSO）算法對(duì)其進(jìn)行求解,。設(shè)計(jì)了一種有效的編碼及解碼方式，因?yàn)榱Ｗ尤核惴ù嬖谄涔逃械脑缡烊毕?，在柔性流水車間調(diào)度問(wèn)題上的應(yīng)用效果還有待提高,，因此本文提出基于位置相似度的鄰域結(jié)構(gòu)，并對(duì)鄰域較優(yōu)粒子采用基于最大完成時(shí)間排序的學(xué)習(xí)方式進(jìn)行鄰域搜索,，改善解的質(zhì)量,，實(shí)驗(yàn)結(jié)果表明本文提出的方法是有效的，有一定的應(yīng)用前景,。

1 具有機(jī)器靈活性的柔性流水車間調(diào)度問(wèn)題描述

　　具有機(jī)器靈活性是指：以柔性流水車間調(diào)度問(wèn)題[2]為基礎(chǔ),，在某道或多道加工工序中存在多用途的機(jī)器，但是該機(jī)器具體用于哪種用途需要在加工開始前確定,，一旦加工開始,，其用途就不可再改變。下面以某飼料廠生產(chǎn)過(guò)程為例介紹,。

　　對(duì)某飼料廠一個(gè)生產(chǎn)車間的生產(chǎn)狀況進(jìn)行調(diào)研以后,，將飼料生產(chǎn)的兩個(gè)主要流程抽取出來(lái)建立一個(gè)調(diào)度模型。飼料在類型上主要分為顆粒飼料和膨化飼料,，其中顆粒飼料分為大顆粒飼料和小顆粒飼料,。所有的飼料在生產(chǎn)過(guò)程中首先要經(jīng)過(guò)配料過(guò)程,，該生產(chǎn)車間共有配料線5條。配料完成后顆粒飼料需要經(jīng)過(guò)制粒機(jī)制成顆粒,，而膨化飼料則需要用膨化機(jī)進(jìn)行膨化,。該車間共有制粒機(jī)5臺(tái)，膨化機(jī)3臺(tái),，其中有1臺(tái)制粒機(jī)只用于制大顆粒,，1臺(tái)制粒機(jī)只用于制小顆粒，其余3臺(tái)制粒機(jī)既可以制大顆粒也可以制小顆粒,。但是為了保證產(chǎn)品質(zhì)量,，生產(chǎn)過(guò)大顆粒的制粒機(jī)不能改制小顆粒，同樣生產(chǎn)過(guò)小顆粒以后也不能再用于生產(chǎn)大顆粒,。

　　該車間的調(diào)度任務(wù)主要有三點(diǎn)：

　?。?）決定3臺(tái)可以制大顆粒飼料也能制小顆粒飼料的制粒機(jī)具體用于哪種用途；

　?。?）制粒機(jī)的用途確定以后即要確定所有產(chǎn)品的加工順序,；

　　（3）決定每種產(chǎn)品在每道工序具體使用哪臺(tái)機(jī)器,。

　　該問(wèn)題為具有機(jī)器靈活性的調(diào)度問(wèn)題,，相比基本的柔性流水車間調(diào)度來(lái)說(shuō)多了一個(gè)選擇機(jī)器用途的步驟，所以難度上有所增加,。

2 粒子群算法介紹

　　粒子群優(yōu)化算法自誕生以來(lái),，在無(wú)約束連續(xù)優(yōu)化領(lǐng)域體現(xiàn)了其巨大的優(yōu)化潛能，該算法結(jié)構(gòu)簡(jiǎn)單,，易于實(shí)現(xiàn),，算法收斂速度快，魯棒性好,。

　　因?yàn)榱Ｗ尤核惴ǖ奶岢鍪菫榱私鉀Q連續(xù)優(yōu)化問(wèn)題,，因此并不能直接用于組合優(yōu)化問(wèn)題的求解。對(duì)此,，本文采用離散粒子群優(yōu)化算法,，根據(jù)粒子群算法的優(yōu)化機(jī)理，離散粒子群算法中粒子采用整數(shù)編碼,，并利用下式來(lái)更新粒子：

　　其中vi（k）和xi（k）表示粒子在第k次迭代時(shí)的速度向量和位置向量,；pbest和gbest分別是粒子的歷史最優(yōu)位置和種群的歷史最優(yōu)位置；表示交叉操作,，具體的交叉方式采用參考文獻(xiàn)[5]中的方法,，對(duì)交叉的兩個(gè)個(gè)體pop1和pop2隨機(jī)選擇交叉區(qū)域，將pop2中的交叉區(qū)域加到pop1中對(duì)應(yīng)的位置，刪除pop1中已在pop2的交叉區(qū)域出現(xiàn)過(guò)的工件,，并進(jìn)行相應(yīng)的映射替換,。

3 問(wèn)題求解

　　3.1 粒子的編碼及解碼

　　利用粒子群算法對(duì)調(diào)度問(wèn)題求解首先要考慮的是粒子的編碼及解碼方式，本文采用基于工序的編碼方式,，即用整數(shù)序列來(lái)表示產(chǎn)品的加工順序,，如一個(gè)加工任務(wù)需要加工5個(gè)產(chǎn)品，則隨機(jī)產(chǎn)生一個(gè)粒子：[2 3 1 4 5],，該編碼表示先加工2號(hào)產(chǎn)品,，再加工3號(hào)產(chǎn)品、1號(hào)產(chǎn)品,、4號(hào)產(chǎn)品,，最后是5號(hào)產(chǎn)品。

　　粒子的編碼方式確定以后,，就需要有解碼方式,，本文采用最先空閑機(jī)器規(guī)則，參考文獻(xiàn)[7]中有定義：在確定的加工優(yōu)先級(jí)的約束下,，機(jī)器無(wú)閑置工件分配規(guī)則是一種最優(yōu)分配模式。因此得到工件加工順序（從第二個(gè)階段開始工件的加工順序由前一加工階段的完成順序決定）后,，需要對(duì)工件在各道工序上的加工順序和加工機(jī)器作出選擇,，最先空閑機(jī)器規(guī)則具體描述見參考文獻(xiàn)[4]。

　　為了解決機(jī)器靈活性問(wèn)題,，本文在原有解碼規(guī)則的基礎(chǔ)上進(jìn)行改進(jìn)：在調(diào)度前,，將多用途的機(jī)器放入一個(gè)集合中，例如common={2,，3,，4}，表示2,、3,、4號(hào)機(jī)器屬于多用途機(jī)器，在最先空閑機(jī)器規(guī)則的第二步中,，如果產(chǎn)品可用common集合中的機(jī)器加工,，則分別計(jì)算產(chǎn)品在集合中各機(jī)器上加工的理論時(shí)間，若結(jié)果顯示要選擇common集合中的機(jī)器來(lái)加工,，則將該機(jī)器從common集合中移除,，并固定用于加工該類產(chǎn)品，依照此思想,，當(dāng)common集合為空時(shí),，所有機(jī)器的用途就確定了，接下來(lái)的產(chǎn)品生產(chǎn)安排可以按照最先空閑機(jī)器規(guī)則來(lái)分配加工機(jī)器。

　　3.2 局部搜索策略

　　單純的粒子群算法容易陷入局部極值,，為使算法能有效地?cái)[脫局部極值的束縛,，進(jìn)行有效的局部搜索是很有必要的。定義粒子相似度：對(duì)兩個(gè)D維的粒子,，其相似度為D′/D,，其中D′表示兩個(gè)粒子有D′維相同。例如對(duì)粒子P1：[3 1 5 4 2]和粒子P2：[3 1 4 2 5],，其相似度為2/5,。

　　有了粒子相似度的概念，規(guī)定粒子的鄰域范圍為與該粒子相似度高于某一閾值的所有粒子,，在此本文采用一種基于最大完成時(shí)間排序的學(xué)習(xí)方式（Makespan Rank Based Learning,，MRBL）進(jìn)行局部搜索，局部搜索的時(shí)機(jī)為種群每更新一次之后,，對(duì)每個(gè)粒子都進(jìn)行一次局部搜索,，具體的搜索方法如下：

　　（1）計(jì)算當(dāng)前粒子與種群其他粒子的相似度,，找出依據(jù)相似度閾值確定的鄰域中適應(yīng)值最優(yōu)的粒子,。

　　（2）計(jì)算鄰域最優(yōu)粒子對(duì)應(yīng)的調(diào)度結(jié)果,，找出完工時(shí)間較大的y個(gè)待加工的產(chǎn)品,，例如完工時(shí)間如表1所示，若取y=2,，則將產(chǎn)品2和產(chǎn)品7從加工序列中移除,，然后依次將產(chǎn)品2和產(chǎn)品7試探性地插入到剩余加工序列的所有可能位置，最后將產(chǎn)品2和產(chǎn)品7放到能最小化最大完工時(shí)間的位置,，得到一個(gè)新的加工序列,。

　　（3）將新得到的序列的適應(yīng)值與原粒子的適應(yīng)值比較,，若優(yōu)于原粒子,，則用新位置更新原粒子位置，否則原粒子不變,。

　?。?）若所有粒子都已進(jìn)行局部搜索，則局部搜索結(jié)束,，否則繼續(xù)對(duì)下一粒子進(jìn)行局部搜索,。

　　步驟（2）中的y值實(shí)際上表示了局部搜索的深度，當(dāng)y值過(guò)大時(shí),，局部搜索的時(shí)間將會(huì)過(guò)長(zhǎng),，甚至讓人無(wú)法接受，而y值過(guò)小，會(huì)導(dǎo)致局部搜索深度不夠,，找到局部更優(yōu)的幾率減小,，因此y的取值在一定程度上會(huì)影響算法效率。參考文獻(xiàn)[8]中采用實(shí)驗(yàn)的方法確定在粒子為50維時(shí)y取6能得到較好的效果,，然而現(xiàn)實(shí)問(wèn)題的維數(shù)是不確定的,，對(duì)每種情況都采用實(shí)驗(yàn)的方法去尋找恰當(dāng)?shù)膟值顯然很不實(shí)際，參考文獻(xiàn)[9]中提到,，考慮到歐式空間多點(diǎn)極限布局,，哈密爾頓回路排列外形近似正方形，因此為平衡局部搜索深度和搜索效率,，本文對(duì)y值進(jìn)行隨機(jī)選取,，其范圍為2~D/4之間，D為問(wèn)題的維數(shù),。

　　3.3 算法流程

　　利用本文算法求解帶機(jī)器靈活性的柔性流水車間調(diào)度問(wèn)題的步驟如下：

　?。?）初始化：設(shè)定粒子群的種群大小和最大迭代次數(shù)，隨機(jī)產(chǎn)生粒子的初始位置,、初始速度和多用途機(jī)器集合common,，以及粒子相似度閾值；

　?。?）求出每個(gè)粒子的適應(yīng)值,，并初始化所有粒子的個(gè)體極值和全局極值；

　?。?）根據(jù)式（1）和式（2）更新粒子位置和粒子速度；

　?。?）求出每個(gè)粒子的適應(yīng)值并更新所有粒子的個(gè)體極值和全局極值,；

　　（5）對(duì)每個(gè)粒子找出其鄰域最優(yōu)粒子,，執(zhí)行一次局部搜索,，并更新粒子個(gè)體極值及全局極值。如果達(dá)到最大迭代次數(shù),，則轉(zhuǎn)步驟（6）,，否則轉(zhuǎn)步驟（3）；

　?。?）結(jié)束算法尋優(yōu)過(guò)程,，輸出最好解。

　　3.4 實(shí)例求解與分析

　　現(xiàn)假設(shè)要同時(shí)生產(chǎn)10種飼料,，其中3種為大顆粒飼料,，2種為小顆粒飼料，其余5種為膨化飼料，各飼料在各工序（機(jī)臺(tái)）上的加工時(shí)間如表2所示,。

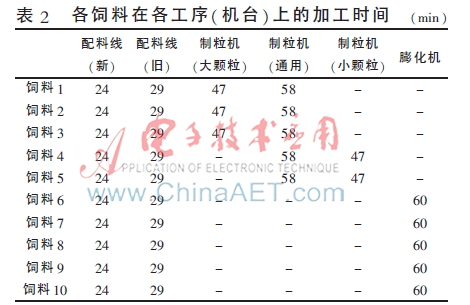
　　其中飼料1~飼料3為大顆粒飼料,，飼料4~飼料5為小顆粒飼料，飼料6~飼料10為膨化飼料,，加工時(shí)間為“-”表示該機(jī)臺(tái)不可用,。

　　為了驗(yàn)證算法的性能，分別利用帶局部搜索的粒子群算法和不帶局部搜索的粒子群算法對(duì)問(wèn)題求解,，種群大小均為40,，迭代次數(shù)均為100次，局部搜索中的相似度閾值取0.85,，兩種算法的迭代曲線圖如圖1所示,。

　　從輸出的調(diào)度結(jié)果得到，common集合為空,，且2臺(tái)通用制粒機(jī)用于制大顆粒飼料,，1臺(tái)通用制粒機(jī)用于制小顆粒飼料，最終的完工時(shí)間為144個(gè)時(shí)間單位,。圖1的迭代曲線顯示,，帶局部搜索的粒子群算法在大約第4次迭代以后就找到了最優(yōu)值，而不帶局部搜索的粒子群算法在大約13次迭代以后才達(dá)到最優(yōu)值,，說(shuō)明本文的算法收斂速度快,，尋優(yōu)精度高。本例中本文算法和不帶局部搜索的粒子群算法在最后的求解精度上沒有區(qū)別,，原因是本例規(guī)模較小,，復(fù)雜度較低，最優(yōu)值很容易找到,。但是相對(duì)于飼料行業(yè)如今普遍使用的手工調(diào)度而言,，本文提出的調(diào)度方法無(wú)論在求解速度上還是求解精度上都有十分出色的表現(xiàn)。

4 結(jié)論

　　本文針對(duì)某飼料廠生產(chǎn)過(guò)程的特點(diǎn)建立了帶機(jī)器靈活性的柔性流水車間調(diào)度模型,，模型中存在加工機(jī)器靈活性也可稱為不確定性,，在傳統(tǒng)的柔性流水車間調(diào)度基礎(chǔ)上要考慮某些機(jī)器的具體用途，機(jī)器用途的選擇不同,，調(diào)度模型也不同,，因此相比基本的柔性流水車間調(diào)度問(wèn)題更有難度。本文利用有效的編碼及解碼方式,，通過(guò)帶局部搜索的粒子群算法對(duì)模型進(jìn)行了有效求解,，求解結(jié)果較好，對(duì)飼料生產(chǎn)調(diào)度有一定指導(dǎo)意義,。然而本文所做的研究有限,，今后還可從編碼及解碼方式以及算法上做更多研究,。

　　參考文獻(xiàn)

　　[1] 王圣堯，王凌,，許燁,，等.求解混合流水車間調(diào)度問(wèn)題的分布估計(jì)算法[J].自動(dòng)化學(xué)報(bào)，2012,，38（3）：437-443.

　　[2] 黎展滔.具有成組約束的柔性流水車間作業(yè)計(jì)劃制定的啟發(fā)式算法[D].廣州：廣東工業(yè)大學(xué),，2012.

　　[3] 周輝仁，唐萬(wàn)生,，魏穎輝.柔性Flow-shop調(diào)度的遺傳算法優(yōu)化[J].計(jì)算機(jī)工程與應(yīng)用,，2009，45（30）：224-226.

　　[4] 王凌,，周剛,，許燁，等.求解不相關(guān)并行機(jī)混合流水線調(diào)度問(wèn)題的人工蜂群算法[J].控制理論與應(yīng)用,，2012,，29（12）：1551-1557.

　　[5] 張其亮，陳永生.基于混合粒子群-NEH算法求解無(wú)等待柔性流水車間調(diào)度問(wèn)題[J].系統(tǒng)工程理論與實(shí)踐,，2014,，34（3）：802-809.

　　[6] 張其亮，陳永生.解決具有混合約束柔性流水車間調(diào)度問(wèn)題的粒子群優(yōu)化算法[J].計(jì)算機(jī)應(yīng)用研究,，2013,，30（11）：3253-3256.

　　[7] 唐立新，吳亞萍.混合流水車間調(diào)度的遺傳下降算法[J].自動(dòng)化學(xué)報(bào),，2002,，28（4）：637-641.

　　[8] 王大志，劉士新,，郭希旺.求解總拖期時(shí)間最小化流水車間調(diào)度問(wèn)題的多智能體進(jìn)化算法[J].自動(dòng)化學(xué)報(bào),，2014，40（3）：548-555.

　　[9] 熊偉,，張江維，張火林.求解TSP問(wèn)題的增強(qiáng)型自探索粒子群算法[J].華北電力大學(xué)學(xué)報(bào),，2009,，36（6）：69-85.