摘  要： 為了使圖像水印算法擁有更好的魯棒性和不可感知性,，以雙樹復(fù)小波變換（DTCWT）為基礎(chǔ),，提出了一種新的彩色圖像盲水印算法,。本算法將彩色圖像顏色空間由RGB轉(zhuǎn)換到Y(jié)IQ，選取亮度分量Y進(jìn)行雙樹復(fù)小波變換,，得到低頻子帶,，然后將加密后的水印信息嵌入到低頻子帶中。在水印提取過程中,，使用了新穎的基于四元數(shù)PHT的最小二乘支持向量（LS-SVM）幾何校正方法,。實(shí)驗(yàn)結(jié)果表明，本算法具有更好的魯棒性和不可感知性,。

　　關(guān)鍵詞： 圖像水?。浑p樹復(fù)小波變換,；四元數(shù)PHT,；幾何校正

0 引言

　　信息技術(shù)的快速發(fā)展使獲取數(shù)字信息更加簡(jiǎn)便，但同時(shí)也帶來了多媒體信息的非法復(fù)制,、篡改等一系列網(wǎng)絡(luò)信息安全問題,，知識(shí)產(chǎn)權(quán)的保護(hù)越來越受到重視，數(shù)字水印技術(shù)應(yīng)運(yùn)而生,?？偟膩碚f，數(shù)字水印技術(shù)就是將有意義的標(biāo)記信息,，通過合適的方法嵌入到宿主信息中,，以達(dá)到版權(quán)保護(hù)、內(nèi)容認(rèn)證,、廣播監(jiān)控等目的,。針對(duì)不同的目的，數(shù)字水印又可以分為魯棒水印和脆弱水印,。魯棒水印技術(shù)主要用來保護(hù)數(shù)字多媒體的所有權(quán),，而脆弱水印技術(shù)對(duì)多媒體信息進(jìn)行身份驗(yàn)證，確保信息的完整性[1],。

　　最近十年,，魯棒圖像水印技術(shù)取得了前所未有的發(fā)展，但是大多數(shù)已存的算法都是圍繞灰度圖像進(jìn)行研究[2],。而日常生活中更為普遍的是能夠提供更多信息的彩色圖像,，因此對(duì)彩色圖像水印技術(shù)的研究尤為重要。參考文獻(xiàn)[3]提出了一種基于人工免疫識(shí)別系統(tǒng)的水印算法,，M位二值序列樣本經(jīng)過人工免疫識(shí)別系統(tǒng)訓(xùn)練后,，嵌入到宿主圖像的藍(lán)色通道中。參考文獻(xiàn)[4]介紹了一種基于支持向量機(jī)（SVM）的彩色圖像水印算法。首先構(gòu)造SVM訓(xùn)練模型,，然后利用模型訓(xùn)練圖像樣本數(shù)據(jù),。參考文獻(xiàn)[5]提出了一種基于支持向量回歸（SVR）和非下采樣輪廓波變換的彩色圖像水印算法，水印被嵌入到宿主圖像的綠色通道,。參考文獻(xiàn)[6]提出了一種基于離散小波變換（DWT）和奇異值分解（SVD）的水印算法，并引入了顏色空間轉(zhuǎn)換,，將顏色空間轉(zhuǎn)換到Y(jié)UV顏色空間,，最終將水印嵌入到小波變換后的HL3區(qū)域的Y、U,、V顏色空間,。

　　上述彩色圖像水印算法都忽略了不同顏色通道之間的正相關(guān)性，其表現(xiàn)必然會(huì)受到影響,，并且在抵抗幾何攻擊方面存在明顯不足,。為解決此問題，展開了許多相關(guān)研究,。參考文獻(xiàn)[7]介紹了一種基于“小波樹”的盲水印技術(shù),，其將像素作為一個(gè)單元，利用小波域中像素之間的相關(guān)性,，通過內(nèi)部像素魯棒性的關(guān)系來攜帶水印信息,，嵌入到宿主圖像。參考文獻(xiàn)[8]提出了一種多尺度傅里葉變換的非盲水印算法,。

　　針對(duì)上述問題,，本文提出了一種基于四元數(shù)PHT和最小二乘支持向量機(jī)（LS-SVM）的新的雙樹復(fù)小波域彩色圖像盲水印算法。實(shí)驗(yàn)證明,，該算法面對(duì)幾何失真具有良好的魯棒性,。該算法的創(chuàng)新性表現(xiàn)在：（1）引入了平移不變性和方向選擇性更好的雙樹復(fù)小波變換；（2）將四元數(shù)PHT應(yīng)用在彩色圖像,，并在水印提取過程中預(yù)算幾何失真的各項(xiàng)校正參數(shù)方面發(fā)揮了重要的作用,。

1 算法思想

　　1.1 雙樹復(fù)小波變換

　　常用的小波變換雖然具有多尺度分析，適應(yīng)人眼的視覺特點(diǎn)等特性,，但是也存在一些缺陷,，比如平移敏感性差、有限的方向選擇性,、缺少相位信息等,。為了克服小波變換的這些缺陷，本文選用雙樹復(fù)小波變換,。雙樹復(fù)小波變換最早由Kingsbury提出,，采用2棵離散小波樹并行地進(jìn)行實(shí)部和虛部運(yùn)算，每一層分解都可以得到2個(gè)低頻子帶（用以進(jìn)行下一層的分解）和6個(gè)不同方向的高頻子帶,。

　　雙樹復(fù)小波變換主要特點(diǎn)可歸納為：（1）具有較好的近似平移不變性,；（2）較好的方向選擇性,。通過雙樹復(fù)小波變換后，圖像在分解的每一層上可獲得6個(gè)方向上的子帶圖像,，這也使得它具有較好的旋轉(zhuǎn)不變性,；（3）較低的重構(gòu)誤差；（4）計(jì)算量小,，實(shí)現(xiàn)效率較高,，能滿足實(shí)時(shí)圖像處理的需要。正是由于這些特性,，雙樹復(fù)小波變換被廣泛應(yīng)用在圖像壓縮編碼,、圖像去噪、圖像檢索等領(lǐng)域,。

　　1.2 最小二乘支持向量機(jī)

　　支持向量機(jī)SVM由Vapnik等人提出,，分類和函數(shù)估計(jì)問題都會(huì)用到SVM，這是建立在統(tǒng)計(jì)學(xué)理論和結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則基礎(chǔ)上的,。Vapnik等人提出的SVM標(biāo)準(zhǔn)算法將訓(xùn)練數(shù)據(jù)分為兩類,，SVM的目標(biāo)是找到一個(gè)最優(yōu)超平面，將任意數(shù)據(jù)點(diǎn)之間的最小距離最大化,。

　　SVM標(biāo)準(zhǔn)算法使用二次規(guī)劃方法,，然而這種方法一般耗時(shí)較長(zhǎng)且很難自適應(yīng)實(shí)現(xiàn)。最小二乘支持向量機(jī)LS-SVM可以解決分類問題和回歸問題,，并且由于LS-SVM某些性質(zhì)與計(jì)算方法相關(guān),，已經(jīng)得到越來越多的關(guān)注。例如,，訓(xùn)練過程需要求解一系列線性方程,，而不是SVM中要解決的二次規(guī)劃問題。Vapnik提出的SVM標(biāo)準(zhǔn)算法中使用的是不等式約束條件,，而LS-SVM使用等式約束條件,。

　　1.3 四元數(shù)PHT

　　根據(jù)四元數(shù)理論[9-10]和灰度圖像PHT[11]的定義，得到彩色圖像四元數(shù)PHT的定義,。假定f（r,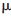，）為極坐標(biāo)下的彩色圖像，定義四元數(shù)PHT如下：

　　根據(jù)正交函數(shù)理論,，可以利用有限個(gè)四元數(shù)PHT值近似重構(gòu)彩色圖像：

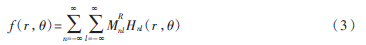
　　1.4 幾何校正

　　針對(duì)圖像水印中由幾何攻擊造成的幾何失真問題,，本文采用基于四元數(shù)PHT的最小二乘支持向量機(jī)（LS-SVM）方法進(jìn)行幾何校正，過程如下,。

　　1.4.1 構(gòu)造訓(xùn)練樣本圖像

　　一般來說,，幾何攻擊包括旋轉(zhuǎn)、縮放和平移等多種形式。首先必須構(gòu)造訓(xùn)練樣本圖像集Hk（k=0,，1,，…，K-1）,，根據(jù)訓(xùn)練樣本圖像集得到LS-SVM訓(xùn)練模型[12],。訓(xùn)練樣本圖像集通過對(duì)含水印彩色圖像進(jìn)行任意參數(shù)的旋轉(zhuǎn)、縮放和平移（包括X方向和Y方向）得到,。

　　1.4.2 LS-SVM訓(xùn)練

　　首先,，對(duì)訓(xùn)練樣本圖像Hk（k=0，1,，…，K-1）進(jìn)行四元數(shù)PHT計(jì)算,，取7個(gè)低階四元數(shù)PHT的幅值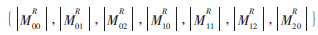作為特征向量進(jìn)行訓(xùn)練,。

　　其次，將旋轉(zhuǎn),、縮放和平移攻擊的參數(shù)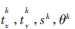（k=0,，1，…,，K-1）作為訓(xùn)練目標(biāo),。tx代表圖像X方向平移距離，ty表示Y方向平移距離,，s表示縮放倍數(shù),，?茲表示旋轉(zhuǎn)的角度。得到如下訓(xùn)練樣本：

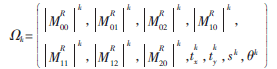
　　其中,，k取0,，1，…,，K-1,。

　　因?yàn)樾D(zhuǎn)、縮放和平移是線性變換,，因此四個(gè)輸出值之間互相沒有影響,，采用4個(gè)LS-SVM平行結(jié)構(gòu)構(gòu)成MIMO系統(tǒng)，平行結(jié)構(gòu)有4個(gè)輸入,，對(duì)訓(xùn)練樣本訓(xùn)練得到LS-SVM模型,。

　　1.4.3 含水印彩色圖像的幾何校正

　　為了精確地提取數(shù)字水印，首先利用LS-SVM訓(xùn)練模型預(yù)測(cè)含水印彩色圖像所受攻擊的參數(shù),，然后對(duì)攻擊圖像進(jìn)行幾何校正來抵抗幾何扭曲,。使用LS-SVM校正含水印彩色圖像的詳細(xì)過程如下：

　　（1）計(jì)算含水印彩色圖像的四元數(shù)PHT值，選取7個(gè)低階四元數(shù)PHT的幅值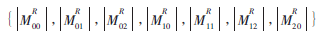作為輸入的特征向量,。

　?。?）使用訓(xùn)練好的LS-SVM訓(xùn)練模型，預(yù)測(cè)得到輸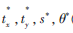出值（幾何變換的參數(shù)）,。

　?。?）利用預(yù)測(cè)出的幾何變換參數(shù)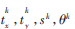對(duì)含水印彩色圖像進(jìn)行幾何校正，得到校正之后的含水印圖像,。

2 算法描述

　　本算法給出一種新的彩色圖像水印算法,，該算法具有較好的視覺質(zhì)量并且能夠有效抵抗幾何扭曲。首先將原始彩色圖像由RGB顏色空間轉(zhuǎn)換為YIQ顏色空間,，然后選取Y分量進(jìn)行雙樹復(fù)小波變換,，取出低頻子帶，將水印嵌入到低頻子帶中,，得到嵌入水印的圖像,。

　　I={R（x，y）,，G（x,，y），B（x,，y）}為彩色宿主圖像,，其中0≤x≤M，0≤y≤N,，R（x,，y）、G（x,，y）和B（x,，y）是彩色圖像在坐標(biāo)（x，y）處的三個(gè)顏色通道,。

　　二值圖像W={w（i,，j），0≤i≤P,，0≤j≤Q}為水印圖像,，用于嵌入宿主圖像，w（i,，j）∈{0,，1}為（i，j）處的像素值,。

　　2.1 水印的嵌入

　?。?）水印預(yù)處理,。為了提高水印算法的安全性，首先對(duì)數(shù)字水印進(jìn)行置亂處理,，本算法使用的是Hilbert曲線置亂,。Hilbert曲線置亂主要思想是：將一個(gè)正方形矩陣四等分，再計(jì)算出每個(gè)子正方形的中心,，將這些中心用直線連接起來,。然后，重復(fù)剛才的步驟,，不斷地細(xì)分下去,。最后，生成了不同遞歸深度的Hilbert曲線,。

　　影響置亂效果的因素主要為置亂路徑和置亂周期,。置亂路徑不同，得到的置亂圖像數(shù)據(jù)序列也不同,。而置亂周期的大小決定了置亂次數(shù)的范圍,。本文選用合適的置亂路徑，將待嵌入的水印圖像置亂500次,，以達(dá)到水印信息加密的目的。

　?。?）原始彩色圖像顏色空間由RGB轉(zhuǎn)換到Y(jié)IQ,。YIQ顏色表示系統(tǒng)由亮度信號(hào)Y和色差信號(hào)I、Q組成,，其主要優(yōu)點(diǎn)是去掉了亮度和顏色信息間的緊密聯(lián)系,，能夠在不影響原始彩色圖像質(zhì)量的情況下處理亮度分量，因此本文選擇YIQ顏色空間,。原始圖像I通過公式（4）,，即可獲得亮度分量Y（x，y）,、色度分量I（x,，y）和飽和度分量Q（x，y）,。

　　YIQ=0.299   0.587   0.1140.596  -0.275  -0.3210.212  -0.523   0.311RGB（4）

　?。?）對(duì)亮度分量Y（x，y）進(jìn)行雙樹復(fù)小波變換,，取出低頻子帶YL（x,，y）。采用最優(yōu)量化公式,，將水印嵌入到低頻子帶YL（x,，y）的系數(shù)yl中,，得到含水印低頻子帶YL′（x，y）的系數(shù)yl′,。水印嵌入公式如下：

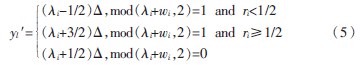
　　其中,，λi=floor（yl/），ri=yl/-λi,，floor為向下取整函數(shù),，mod為模運(yùn)算函數(shù)，為量化步長(zhǎng),，wi為待嵌入的原始水印,。

　　（4）含水印低頻子帶YL′（x,，y）進(jìn)行雙樹復(fù)小波逆變換,，得到含水印的亮度分量Y′（x，y）,，結(jié)合上述步驟（2）中產(chǎn)生的I（x,，y）和Q（x，y）,，利用公式（6）將顏色空間轉(zhuǎn)回到RGB,，于是得到含水印的彩色圖像I′。

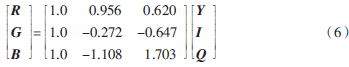
　　2.2 含水印圖像校正

　　利用四元數(shù)PHT進(jìn)行幾何校正,，可以有效抵抗旋轉(zhuǎn),、平移、縮放等幾何攻擊,。詳細(xì)步驟見本文1.4節(jié),，概括如下：

　　（1）訓(xùn)練樣本圖像進(jìn)行四元數(shù)PHT計(jì)算,，選取低7階四元數(shù)PHT幅值作為有效的圖像特征向量,。

　　（2）選取合適的核函數(shù)進(jìn)行訓(xùn)練,，得到LS-SVM訓(xùn)練模型,。

　　（3）根據(jù)LS-SVM訓(xùn)練模型,，對(duì)旋轉(zhuǎn),、平移、縮放攻擊后的待檢測(cè)含水印彩色圖像I′進(jìn)行校正,。

　　2.3 水印的提取

　　本文提出的水印提取算法不需要原始彩色圖像和其他信息,，屬于盲水印技術(shù)。用I″表示校正之后的含水印彩色圖像,，提取的詳細(xì)步驟如下：

　?。?）對(duì)校正后的含水印彩色圖像I″進(jìn)行顏色空間轉(zhuǎn)換,，由RGB轉(zhuǎn)換到Y(jié)IQ，獲取亮度分量Y″（x,，y）,。

　　（2）對(duì)得到的亮度分量Y″（x,，y）進(jìn)行雙樹復(fù)小波變換,，取出低頻子帶YL″（x，y）,，其系數(shù)為yl″,。

　　（3）在低頻子帶中,，利用量化公式提取水印wi′,。公式如下：

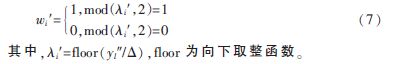
　　（4）將提取出的水印信息進(jìn)行反Hilbert曲線置亂500次,，即可得到原始水印信息,。

3 實(shí)驗(yàn)仿真

　　本文以24位Lena（512×512 bit）真彩色圖像為載體圖像，以標(biāo)有花朵（64×64 bit）的二值圖像為水印圖像,，在MATLAB R2012a環(huán)境下進(jìn)行了仿真,。實(shí)驗(yàn)時(shí)選取量化步長(zhǎng)?駐為12，雙樹復(fù)小波變換為二級(jí)變換,，訓(xùn)練樣本的數(shù)目K為50,。

　　在數(shù)字水印實(shí)驗(yàn)中，一般選取峰值信噪比PSNR作為衡量水印不可感知性的主要標(biāo)準(zhǔn),，PSNR值越大，含水印圖像越接近原始載體圖像,；選取誤碼率BER衡量提取出水印的準(zhǔn)確程度,，BER值越接近0，則表示提取出的水印越接近于原始水印,。PSNR和BER的表達(dá)式分別如式（8）和式（9）所示,。

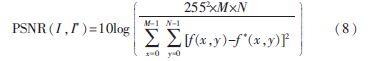
　　其中，I為原始彩色圖像,，I*為含水印彩色圖像,，M×N為圖像的尺寸。

　　其中,，B為提取出水印中錯(cuò)誤的bit數(shù),，P×Q為水印的尺寸。

　　3.1 算法的不可感知性

　　為了測(cè)試算法的不可感知性,，本文選取含水印的圖像Lena,、Barbara和Mandrill展開實(shí)驗(yàn),，并將結(jié)果與參考文獻(xiàn)[13]相比較，結(jié)果如表1,。從表1中不難看出,，算法具有良好的不可感知性。

　　3.2 算法的魯棒性

　　為了驗(yàn)證算法的魯棒性,，本文針對(duì)各種攻擊手段進(jìn)行了測(cè)試,。由于本文算法創(chuàng)新性地提出了基于四元數(shù)PHT和最小二乘支持向量機(jī)LS-VSM的幾何校正方法，故重點(diǎn)針對(duì)旋轉(zhuǎn),、平移,、縮放等幾何攻擊進(jìn)行了測(cè)試，并與參考文獻(xiàn)[13],、[4]進(jìn)行了對(duì)比,，實(shí)驗(yàn)結(jié)果如表2、表3,。

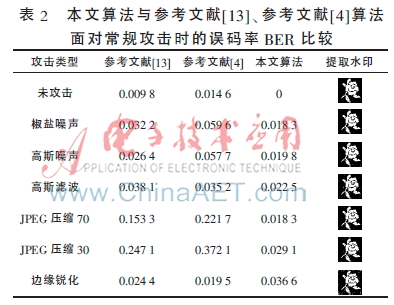
　　由表2和表3中參考文獻(xiàn)[13],、[4]算法與本文算法的實(shí)驗(yàn)結(jié)果對(duì)比可知，本文算法在面對(duì)各種攻擊,，尤其是旋轉(zhuǎn),、平移、縮放等幾何攻擊時(shí),，具有遠(yuǎn)超過參考文獻(xiàn)[13],、[4]的效果。這正是由于本文創(chuàng)新性地引入了四元數(shù)PHT以及構(gòu)造最小二乘支持向量機(jī)模型,，對(duì)旋轉(zhuǎn),、平移、縮放攻擊后的失真圖像進(jìn)行了幾何校正,。然后,，從經(jīng)過幾何校正的含水印的彩色圖像中提取水印。從表2中還會(huì)發(fā)現(xiàn),，算法在面對(duì)加噪聲,、濾波、JPEG壓縮等常規(guī)攻擊時(shí),，效果也要好于文獻(xiàn)[13],、[4]的算法，這是由于本文采用了平移不變性和方向選擇性更好的雙樹復(fù)小波變換,，并成功將水印信息嵌入到其低頻子帶,。

4 結(jié)論

　　針對(duì)幾何失真的魯棒彩色圖像水印算法的研究是一項(xiàng)具有挑戰(zhàn)性的工作。本文提出了一種基于四元數(shù)PHT的最小二乘支持向量（LS-SVM）幾何校正的魯棒水印算法,。實(shí)驗(yàn)表明,，該算法在面對(duì)旋轉(zhuǎn),、平移、縮放等幾何失真時(shí),，可以進(jìn)行有效的校正,，以達(dá)到準(zhǔn)確提取水印的目的。該算法的創(chuàng)新性表現(xiàn)在：（1）引入了平移不變性和方向選擇性更好的雙樹復(fù)小波變換,；（2）將四元數(shù)PHT應(yīng)用在彩色圖像,，并在水印提取過程中，在預(yù)算幾何失真的各項(xiàng)校正參數(shù)方面發(fā)揮了重要的作用,。本文的不足之處體現(xiàn)在,，LS-SVM訓(xùn)練模型和四元數(shù)PHT的計(jì)算稍復(fù)雜，耗時(shí)方面仍待提高,。

　　參考文獻(xiàn)

　　[1] BIANCHI T. Secure watermarking for multimedia content protection： a review of its benefits and open issues[J]. IEEE Signal Processing Magazine,， 2013，30（2）：87-96.

　　[2] ZHANG H,， SHU H,， COATRIEUX G. Affine Legendre moment invariants for image watermarking robust to geometric distortions[J]. IEEE Trans Image Process， 2011,，20（8）：2189-2199.

　　[3] OGUZ F,， ISMAIL B， ?譈LKER E. A color image watermarking scheme based on artificial immune recognition system[J]. Expert Syst Appl,， 2011,，38（3）：1942-1946.

　　[4] TSAI H H， SUN D W. Color image watermark extraction based on support vector machines[J]. Information Sciences,， 2007,，177（2）：550-569.

　　[5] NIU P P， WANG X Y,， YANG Y P,， et al. A novel color image watermarking scheme in nonsampled contourlet-domain[J]. Expert Systems With Applications，2011,，38（3）： 2081-2098.

　　[6] GUNJAL B L,， MALI S N. Strongly robust and highly secured DWT-SVD based color image watermarking： embedding data in all Y,， U. V color spaces[J]. Int J Inform Technol Comput Science,， 2012，4（3）：1-7.

　　[7] AL-OTUM H M,， SAMARA N A. A robust blind color image watermarking based on wavelet-tree bit host difference selection[J]. Signal Process,， 2010，90（8）：2498-2512.

　　[8] TSUI T K,， ZHANG X P,， ANDROUTSOS D. Color image watermarking using multidimensional Fourier transforms[J]. IEEE Trans Inform Forensics Secur,， 2008，3（1）：16-28.

　　[9] CHEN B J,， SHU H Z,， ZHANG H， et al. Quaternion Zernike moments and their invariants for color image analysis and object recognition[J]. Signal Processing,， 2012,，92（2）：308-318.

　　[10] GUO L Q， ZHU M. Quaternion Fourier-Mellin moments for color images[J]. Pattern Recognition,， 2011,，44（2）： 187-195.

　　[11] YAP P T， JIANG X D,， KOT A C. Two-dimensional polar harmonic transforms for invariant image representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence,， 2010， 32（7）： 1259-1270.

　　[12] 徐紫涵,，王向陽.可有效抵抗一般性幾何攻擊的數(shù)字水印檢測(cè)方法[J].自動(dòng)化學(xué)報(bào),，2009，35（1）：23-27.

　　[13] FU Y G,， SHEN R M. Color image watermarking schemo based on linear discriminant analysis[J]. Computer Standards & Interfaces,， 2008， 30（3）：115-120.