摘  要： 提出了一種新的圖像融合算法——基于邊緣檢測(cè)的雙樹復(fù)小波圖像融合算法,。多聚焦圖像經(jīng)過(guò)雙樹復(fù)小波變換較好地克服了傳統(tǒng)小波變換的平移敏感性等缺點(diǎn),；低頻系數(shù)利用邊緣信息進(jìn)行融合，較好地保留了圖像的細(xì)節(jié)信息,，提高了融合圖像的質(zhì)量,；高頻系數(shù)則采用常見(jiàn)的基于區(qū)域特征的融合規(guī)則,。實(shí)驗(yàn)結(jié)果證明，該算法能夠有效地提高融合圖像的清晰度,，細(xì)節(jié)更為豐富,。

　　關(guān)鍵詞： 圖像融合；雙樹復(fù)小波變換,；邊緣檢測(cè)

0 引言

　　圖像融合[1-3]指對(duì)多幅源自于同一場(chǎng)景的圖像進(jìn)行綜合,，以獲取更好的視覺(jué)效果和易于機(jī)器識(shí)別為目的，產(chǎn)生比單一信源更精確,、更完全,、更可靠的圖像。圖像融合屬于信息融合的一個(gè)分支,，能夠有效地去除參與融合的多幅圖像中冗余或干擾信息,，反映多幅源圖像的信息，使獲得的圖像更加準(zhǔn)確,、完整,，便于更綜合、全面地判斷和分析圖像,，彌補(bǔ)了單一成像系統(tǒng)的不足,。20世紀(jì)70年代后期提出圖像融合概念后，國(guó)內(nèi)外對(duì)圖像融合算法的研究以及相關(guān)應(yīng)用的探討已取得了長(zhǎng)足的發(fā)展,。圖像融合處理可在像素級(jí),、特征級(jí)以及決策級(jí)三個(gè)層面上進(jìn)行，圖像的像素級(jí)融合主要可分為兩類：基于空域和基于變換域,。隨著小波變換理論的完善,，基于小波的圖像融合方法已成為國(guó)內(nèi)外像素級(jí)圖像融合方法的研究熱點(diǎn)[4-7]。目前,，大多數(shù)的小波變換圖像融合算法主要是針對(duì)高頻信息的融合規(guī)則進(jìn)行討論,，對(duì)低頻信息僅采取簡(jiǎn)單的加權(quán)平均融合規(guī)則。然而,，圖像經(jīng)過(guò)小波變換后,，主要的能量都包含在低頻信息中,，融合的質(zhì)量很大程度上都取決于低頻信息融合規(guī)則的選取,。因此，對(duì)低頻信息的融合規(guī)則研究具有相當(dāng)重要的意義,。

　　傳統(tǒng)的離散小波變換（DWT）存在平移敏感性和缺乏方向選擇性等缺陷,，嚴(yán)重地影響了小波域信號(hào)處理效果。IVAN W S[8]等人提出的雙樹復(fù)小波變換（DT-CWT）成功地解決了傳統(tǒng)DWT的缺陷,，并已成功應(yīng)用于圖像融合領(lǐng)域[9-11],。本文針對(duì)雙樹復(fù)小波變換以及低頻信息融合規(guī)則進(jìn)行研究,，提出了一種新的圖像融合算法——基于邊緣檢測(cè)的雙樹復(fù)小波圖像融合算法。該算法能夠有效提高圖像融合的清晰度及質(zhì)量,。

1 雙樹復(fù)小波變換

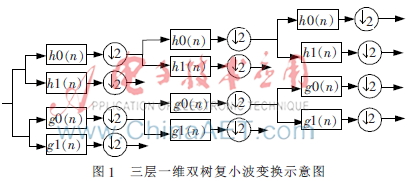
　　雙樹復(fù)小波變換（DT-CWT）結(jié)構(gòu)示意圖如圖1所示,。當(dāng)對(duì)應(yīng)小波基（圖1中的h0和g0、h1和g1）近似滿足Hilbert變換關(guān)系時(shí),，雙樹復(fù)小波變換能夠近似滿足平移不變性,，并具有良好的方向選擇性。在二維雙樹復(fù)小波變換中實(shí)部與虛部都具有6個(gè)方向子帶,，分別指向±15°,，±45°和±75°方向。這些優(yōu)點(diǎn)使雙樹復(fù)小波變換為圖像融合提供了更好的條件,。

2 融合規(guī)則

　　基于小波變換的圖像融合方法基本思想如圖2所示,。先對(duì)源圖像進(jìn)行小波分解，得到不同頻率的不同特征域的圖像表示,，在各個(gè)特征域上選取不同的融合規(guī)則或融合方法進(jìn)行圖像的融合,，融合后得到新的小波系數(shù)經(jīng)逆小波變換得到融合后的圖像。

　　2.1 低頻信息融合規(guī)則

　　圖像經(jīng)過(guò)小波變換后,，其主要能量集中在低頻區(qū)域中,，傳統(tǒng)的加權(quán)平均選取融合算法可以有效地抑制圖像噪聲，但圖像邊緣特征信息卻被忽略,，造成融合圖像的特征信息丟失,、融合圖像質(zhì)量下降。本文在傳統(tǒng)小波圖像融合基礎(chǔ)上,，對(duì)傳統(tǒng)的低頻系數(shù)加權(quán)平均算法進(jìn)行改進(jìn),，提出了基于邊緣檢測(cè)的低頻系數(shù)圖像融合方法。該算法在多源圖像中最大可能地選取邊緣點(diǎn)加以保留,，可使融合后圖像的細(xì)節(jié)更加豐富,。經(jīng)典的邊緣檢測(cè)算子包括Sobel算子、Roberts算子,、Canny算子,、Laplacian算子以及Prewitt算子等，這些算子均在像素級(jí)上進(jìn)行圖像邊緣檢測(cè),，并且都有一定的局限性,。例如，Laplacian算子雖然對(duì)細(xì)線和孤立點(diǎn)的檢測(cè)效果較好,，但對(duì)噪聲比較敏感,；Prewitt和Sobel算子則是對(duì)漸變灰度和低噪聲效果顯著，但是檢測(cè)邊緣較粗且定位較差,。Zernike正交矩的亞像素邊緣檢測(cè)方法[12-13]的提出很大程度上提高了邊緣檢測(cè)的精準(zhǔn)度,。本文利用Zernike正交矩的亞像素邊緣檢測(cè)方法對(duì)圖像小波分解后的低頻信息進(jìn)行邊緣檢測(cè),，獲取最佳邊緣信息。

　　具體融合規(guī)則如下：

　?。?）設(shè)A和B分別為待融合的源圖像,，對(duì)圖像A和B分別進(jìn)行雙樹復(fù)小波變換（DT-CWT），得到各自的高頻分量hAj,、hBj和低頻分量lAj,、lBj，其中j為小波分解級(jí)數(shù),。

　?。?）分別對(duì)兩幅源圖像的小波分解后低頻分量lAj、lBj進(jìn)行邊緣檢測(cè),，得到低頻系數(shù)的邊緣圖像EWAj和EWBj（二值邏輯圖）,，邊緣檢測(cè)算法采用Zernike正交矩的亞像素邊緣檢測(cè)方法。

　?。?）對(duì)低頻系數(shù)的邊緣圖像EWAj和EWBj進(jìn)行判斷,，判斷規(guī)則如下：如果兩幅邊緣圖像相同位置上的值相等，即EWAj（x,，y）=EWBj（x,，y），根據(jù)式（1）和式（2）修改邊緣圖像的值,；其余不變,。

　　2.2 高頻信息融合規(guī)則

　　圖像經(jīng)過(guò)小波分解后，低頻分量反映了圖像的基本概貌,，高頻分量則突出了圖像的細(xì)節(jié)信息,。由于圖像的局域特征往往不能由單一像素所表征，因此,，基于區(qū)域特征的融合規(guī)則也一直是研究的熱點(diǎn),。本文選取兩種基于區(qū)域特征的融合規(guī)則對(duì)高頻信息進(jìn)行融合：區(qū)域能量最大值法和區(qū)域邊緣強(qiáng)度最大值法。

　　第k個(gè)源圖像的高頻小波系數(shù)中以（x,，y）為中心,、大小為M×N的區(qū)域的能量ENj（x，y）表示為：

　　區(qū)域中值定義為：

　　則第k個(gè)圖像的像素（x,，y）在j尺度下,，窗口大小為M×N的邊緣強(qiáng)度[3]定義為：

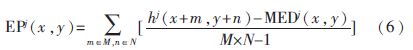
　　本文所選取的兩種區(qū)域特征融合算法的窗口大小均為3×3，兩種高頻系數(shù)具有如下融合規(guī)則：

　　方法1：區(qū)域能量最大值法

　　Fh=dA×hA+dB×hB（7）

　　其中,，hA和hB分別代表源圖像A和B的高頻系數(shù),，F(xiàn)h表示融合后的高頻小波系數(shù),，dA和dB則為權(quán)系數(shù),，取值為：

　　dA=1  |ENA|≥|ENB|0  其他（8）

　　dB=1-dA

　　方法2：區(qū)域邊緣強(qiáng)度最大值法

　　基于區(qū)域邊緣強(qiáng)度最大值法的基本思路與區(qū)域能量最大值法一致,，在兩個(gè)源圖像的高頻小波系數(shù)中根據(jù)區(qū)域邊緣強(qiáng)度的大小來(lái)選擇誰(shuí)作為融合后的小波系數(shù)。區(qū)別僅在于權(quán)系數(shù)的取值準(zhǔn)則不同：

　　dA=1  |EPA|≥|EPB|0  其他（9）

　　dB=1-dA

3 實(shí)驗(yàn)結(jié)果與分析

　　本文選取常見(jiàn)的多聚焦圖像cameraman進(jìn)行融合,，為了驗(yàn)證所提出的融合算法的有效性與優(yōu)越性,，采用以下4種方法對(duì)比本文所提出的算法的性能。

　　方法1：低頻系數(shù)采取加權(quán)平均法,，高頻系數(shù)選用區(qū)域能量最大法進(jìn)行融合,。

　　方法2：低頻系數(shù)采取邊緣檢測(cè)法，高頻系數(shù)選用區(qū)域能量最大法進(jìn)行融合,。

　　方法3：低頻系數(shù)采取加權(quán)平均法,，高頻系數(shù)選用區(qū)域邊緣強(qiáng)度最大值法。

　　方法4：低頻系數(shù)采取邊緣檢測(cè)法,，高頻系數(shù)選用區(qū)域邊緣強(qiáng)度最大值法,。

　　實(shí)驗(yàn)中采用的融合評(píng)測(cè)方法有熵、峰值信噪比（PSNR）,、平均梯度以及標(biāo)準(zhǔn)差,。熵值越大，表明所含信息量越大,；PSNR越大,，表明所獲取的信息越多、噪聲越小,，融合的效果也越好,；平均梯度越大，表明圖像的細(xì)節(jié)部分越豐富,，圖像清晰度越高,；標(biāo)準(zhǔn)差越大，表明圖像灰度值相對(duì)于圖像均值越分散,，圖像的反差越大,，所包含的圖像信息量越多。

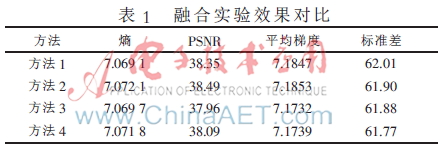
　　表1列出了本文所采取的4種方法的融合效果,。圖3展示出了效果最好的方法2的融合效果圖,。對(duì)比這4種方法的各項(xiàng)指標(biāo)不難發(fā)現(xiàn)，方法2的熵值,、PSNR以及平均梯度3個(gè)指標(biāo)均優(yōu)于其他方法,，標(biāo)準(zhǔn)差基本一致。從實(shí)驗(yàn)結(jié)果可看出,，高頻系數(shù)選用相同融合規(guī)則時(shí),，低頻系數(shù)采用邊緣檢測(cè)方法進(jìn)行融合效果較好，說(shuō)明本文提出的基于邊緣檢測(cè)的融合算法具有一定的優(yōu)越性，邊緣與細(xì)節(jié)信息保留較好,。低頻系數(shù)的選擇決定了融合圖像的視覺(jué)效果,，采用本文算法可更大限度地獲取并保留圖像的細(xì)節(jié)與紋理信息，增強(qiáng)融合圖像的質(zhì)量,。

4 結(jié)論

　　本文提出了一種新的圖像融合算法——基于邊緣檢測(cè)的雙樹復(fù)小波圖像融合算法,。采用雙樹復(fù)小波變換，可有效克服傳統(tǒng)離散小波變換存在的平移敏感性和缺乏方向選擇性等缺陷,；低頻系數(shù)融合規(guī)則結(jié)合了邊緣檢測(cè)的方法來(lái)降低邊緣細(xì)節(jié)信息的丟失,，提高圖像融合的清晰度及質(zhì)量；高頻系數(shù)采用常見(jiàn)的區(qū)域能量最大法以及區(qū)域邊緣強(qiáng)度最大值法進(jìn)行融合,。實(shí)驗(yàn)結(jié)果利用4個(gè)客觀評(píng)價(jià)標(biāo)準(zhǔn)進(jìn)行定性衡量,，證明了本文算法的有效性和正確性。

參考文獻(xiàn)

　　[1] POHL C,， VAN GENDEREN J L. Multisensor image fusion in remote sensing： concepts,， methods and applications[J]. International Journal of Remote Sensing， 1998,，19（5）：823- 854.

　　[2] 郭雷,，李暉暉，鮑永生.圖像融合[M].北京：電子工業(yè)出版社,，2008.

　　[3] 閆敬文.數(shù)字圖像處理MATLAB版（第二版）[M].北京：國(guó)防工業(yè)出版社,，2011.

　　[4] 劉海濤，石躍祥,，康蘊(yùn).基于小波分析的圖像融合新方法[J].計(jì)算機(jī)工程與應(yīng)用,，2013，49（6）：205-208.

　　[5] Zhang Qiang. Multi-focus image fusion using the nonsubsampled Contourlet transform[J]. Signal Processing,，2009,，89（7）：1334-1346.

　　[6] Chen Guangqiu， Gao Yinhan. Multisource image fusion based on double density dual-tree complex wavelet transform[C]. International Conference on Fuzzy Systems and Knowledge Discovery （FSKD）,， 2012： 1864-1868.

　　[7] 吳華,，王海順.基于小波變換和Sobel算子圖像融合算法研究[J].計(jì)算機(jī)仿真，2011,，28（10）：232-235.

　　[8] IVAN W S,， RICHARD G B， NICK G K. The dual-tree complex wavelet transform[J]. IEEE Signal Processing Magazine,， 2005,， 11（22）： 123-151.

　　[9] HILL P， CANAGARAJAH N,， BULL D. Image fusion using complex wavelets[C]. Proceedings of the British Machine Conference,， Cardiff， 2002： 487-496.

　　[10] 王亞杰，李殿起,，徐心和.基于雙樹復(fù)小波變換的圖像融合方法[J].計(jì)算機(jī)工程,，2008，34（15）：176-178.

　　[11] 陶玲瑤,，弓曉鋒.基于DT-CWT的圖像融合算法研究[J].通信技術(shù),，2011,，44（12）：104-106.

　　[12] GHOSAL S,， MEHROTRA R. Orthogonal moment operators for subpixel edge detection[J]. Pattern Recognition， 1993,， 26： 295-306.

　　[13] Ding Xinghao,， Deng Shanxi， Yang Yongyue,， et al. Sub-pixel detection based on spatial moment and Zernike moment[J]. Journal of Applied Sciences,，2004，22（2）：191-194.