摘 要: 提出了一種直接序列擴(kuò)頻信號(hào)(Direct Sequence Spread Spectrum,,DS-SS)的盲同步算法,該算法采用自相關(guān)矩陣的譜范數(shù)進(jìn)行失步點(diǎn)估計(jì),,簡(jiǎn)單有效,、誤差小。理論分析及計(jì)算機(jī)仿真結(jié)果表明,,該算法在低信噪比條件下可實(shí)現(xiàn)DS-SS信號(hào)的盲同步,,進(jìn)而可用于對(duì)直擴(kuò)信號(hào)的參數(shù)估計(jì)。
關(guān)鍵詞: 盲同步,;直接序列擴(kuò)頻信號(hào),;偽隨機(jī)序列
0 引言
直接序列擴(kuò)頻信號(hào)(DS-SS)由于具有一系列獨(dú)特的優(yōu)點(diǎn),,比如抗噪聲、抗干擾,、抗多徑衰落,、能在低功率譜密度下工作、有保密性,、可多址復(fù)用和任意選址,、測(cè)量精度高等,目前已經(jīng)被廣泛應(yīng)用于軍事通信,、衛(wèi)星導(dǎo)航等系統(tǒng)中,。在非協(xié)作通信系統(tǒng)中,與之對(duì)應(yīng)的信息偵測(cè)技術(shù),,尤其是直擴(kuò)信號(hào)的盲估計(jì)成為目前研究的熱點(diǎn),,參考文獻(xiàn)[1-2]對(duì)DS-SS信號(hào)盲解擴(kuò)方法進(jìn)行了探討。
實(shí)現(xiàn)信號(hào)的盲估計(jì)需要事先完成信號(hào)的盲同步,。為了檢測(cè)接收信號(hào)的起點(diǎn),,參考文獻(xiàn)[3]提出一種基于協(xié)方差矩陣Frobenius范數(shù)最大化的盲同步方法,,在低信噪比條件下具有優(yōu)越的估計(jì)性能,,然而其計(jì)算復(fù)雜度較大,特別是在擴(kuò)頻波形周期較大情況下性能下降嚴(yán)重,。本文提出一種利用矩陣譜范數(shù)的直擴(kuò)信號(hào)盲同步方法,,能夠比Frobenius范數(shù)法進(jìn)一步提高同步估計(jì)精度。
1 DS-SS信號(hào)模型
假設(shè)接收信號(hào)為擴(kuò)頻周期已知的基帶直擴(kuò)信號(hào),,并且被白噪聲污染,,可表示為:

其中,ak為相互獨(dú)立且等概率隨機(jī)分布的信息碼序列,,碼元寬度為Ts,;n(t)為零均值加性高斯白噪聲;h(t)為擴(kuò)頻波形,,它是一個(gè)完整周期的擴(kuò)頻序列基帶信號(hào)與傳輸鏈路的等效傳遞函數(shù)的卷積:

其中,,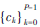 為擴(kuò)頻碼序列,碼元寬度為Tc,,P為擴(kuò)頻碼長(zhǎng)且有P=Ts/Tc,;p(t)代表發(fā)射、信道沖擊響應(yīng)以及接收濾波器的綜合卷積,。
為擴(kuò)頻碼序列,碼元寬度為Tc,,P為擴(kuò)頻碼長(zhǎng)且有P=Ts/Tc,;p(t)代表發(fā)射、信道沖擊響應(yīng)以及接收濾波器的綜合卷積,。
不失一般性,,本文做如下假設(shè):信息序列為均勻分布且互不相關(guān);噪聲為零均值高斯白噪聲,,且與信號(hào)不相關(guān),。
2 基于譜范數(shù)的盲同步方法
假設(shè)信息碼時(shí)寬Ts已經(jīng)利用已有方法估計(jì)得到,,例如可用參考文獻(xiàn)[4]的方法,因此可假設(shè)Ts為已知,。設(shè)采樣率為Te,,接收的信號(hào)經(jīng)采樣后得到的信號(hào)矢量記作y:
y=[s(0),s(Te),,…,,s((j-1)Te)](3)
其中j=1,2,,…
現(xiàn)在目的是尋找y中對(duì)應(yīng)的第一個(gè)信息碼的采樣點(diǎn),,具體方法如下:將數(shù)據(jù)劃分為N個(gè)互不重疊的數(shù)據(jù)段,每個(gè)數(shù)據(jù)段長(zhǎng)度為Ts,,也可認(rèn)為是在信號(hào)中加入N個(gè)寬度為Ts的相鄰分析窗,。每個(gè)分析窗中包含M個(gè)采樣點(diǎn),即Ts=MTe,。
設(shè)數(shù)據(jù)的失步時(shí)間t0為d個(gè)采樣周期,,即t0=d×Te,d∈[0,,M-1],,觀察第k個(gè)分析窗,該窗內(nèi)數(shù)據(jù)可用M維矢量yd,,k表示為:
yd,,k=[s((d+(k-1)M+1)Ts),…,,s((d+kM)Ts)](4)
在此基礎(chǔ)上,,將N段數(shù)據(jù)按順序作為列向量,構(gòu)造M×N階矩陣:
Y=[yd,,1,,…,yd,,N](5)
為降低噪聲的影響,,采用Y的自相關(guān)矩陣進(jìn)行分析,該自相關(guān)矩陣為:
R=E{YYH}(6)
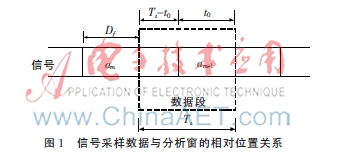
圖1給出了同步前接收信號(hào)與數(shù)據(jù)分析窗之間的位置關(guān)系,,其中t0為分析窗與信息碼符號(hào)起始位置之間的時(shí)間差,。同步的目的是通過改變分析窗的位置,使得分析窗位于信息碼的起始位置,,以便于對(duì)信號(hào)的后續(xù)處理,。
實(shí)際應(yīng)用中計(jì)算R的常用方法是計(jì)算其估計(jì)值![$F]4@3~3I154PZ52P]P21QP.jpg $F]4@3~3I154PZ52P]P21QP.jpg](http://files.chinaaet.com/images/2016/02/24/6359193750551100004311459.jpg) [5],。
[5],。

參考文獻(xiàn)[4]指出,,當(dāng)![$F]4@3~3I154PZ52P]P21QP.jpg $F]4@3~3I154PZ52P]P21QP.jpg](http://files.chinaaet.com/images/2016/02/24/6359193751582000001858190.jpg) 的特征值λ1最大時(shí),,意味著信號(hào)的失步時(shí)間為0。因此估計(jì)失步時(shí)間相當(dāng)于尋找使得特征值λ1最大的自相關(guān)矩陣,。而當(dāng)λ1最大時(shí),,
的特征值λ1最大時(shí),,意味著信號(hào)的失步時(shí)間為0。因此估計(jì)失步時(shí)間相當(dāng)于尋找使得特征值λ1最大的自相關(guān)矩陣,。而當(dāng)λ1最大時(shí),,![$F]4@3~3I154PZ52P]P21QP.jpg $F]4@3~3I154PZ52P]P21QP.jpg](http://files.chinaaet.com/images/2016/02/24/6359193752332400004374210.jpg) 的Frobenius范數(shù)的平方
的Frobenius范數(shù)的平方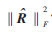 達(dá)到最大值,‖·‖F(xiàn)表示矩陣的Frobenius范數(shù),。參考文獻(xiàn)[3]正是通過移動(dòng)分析窗使得
達(dá)到最大值,‖·‖F(xiàn)表示矩陣的Frobenius范數(shù),。參考文獻(xiàn)[3]正是通過移動(dòng)分析窗使得 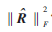 最大,,從而使得分析窗位于信號(hào)的起始點(diǎn),從而實(shí)現(xiàn)同步,。
最大,,從而使得分析窗位于信號(hào)的起始點(diǎn),從而實(shí)現(xiàn)同步,。
根據(jù)矩陣?yán)碚揫6],,在有噪聲擾動(dòng)的情況下,對(duì)于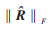 ,,擾動(dòng)產(chǎn)生的誤差下界為P2,,顯然當(dāng)擴(kuò)頻碼長(zhǎng)度P較長(zhǎng)時(shí),誤差將明顯增大,,同步點(diǎn)位置估計(jì)性能會(huì)顯著下降,。因此本文采用其他方法來估計(jì)失步時(shí)間。
,,擾動(dòng)產(chǎn)生的誤差下界為P2,,顯然當(dāng)擴(kuò)頻碼長(zhǎng)度P較長(zhǎng)時(shí),誤差將明顯增大,,同步點(diǎn)位置估計(jì)性能會(huì)顯著下降,。因此本文采用其他方法來估計(jì)失步時(shí)間。
在矩陣?yán)碚撝?,另一常用的算子范?shù)為譜范數(shù),,表示為‖·‖2,譜范數(shù)計(jì)算方法為求矩陣的最大特征值,。對(duì)于![UJ]FU6_M3MD26(EB~H@}ZJC.jpg UJ]FU6_M3MD26(EB~H@}ZJC.jpg](http://files.chinaaet.com/images/2016/02/24/6359193767084500008033630.jpg) ,,λi表示矩陣的特征值,。在受同樣噪聲擾動(dòng)的情況下,,對(duì)于譜范數(shù)‖
,,λi表示矩陣的特征值,。在受同樣噪聲擾動(dòng)的情況下,,對(duì)于譜范數(shù)‖![$F]4@3~3I154PZ52P]P21QP.jpg $F]4@3~3I154PZ52P]P21QP.jpg](http://files.chinaaet.com/images/2016/02/24/6359193768022000001371343.jpg) ‖2,擾動(dòng)產(chǎn)生的誤差下界為
‖2,擾動(dòng)產(chǎn)生的誤差下界為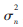 ,,明顯小于Frobenius范數(shù),。因此本文使用
,,明顯小于Frobenius范數(shù),。因此本文使用![$F]4@3~3I154PZ52P]P21QP.jpg $F]4@3~3I154PZ52P]P21QP.jpg](http://files.chinaaet.com/images/2016/02/24/6359193771961500004369476.jpg) 的譜范數(shù)來尋找信息碼的起點(diǎn)。顯然,,當(dāng)移動(dòng)分析窗使得信號(hào)達(dá)到同步時(shí),,其自相關(guān)矩陣的譜范數(shù)也會(huì)達(dá)到最大。綜上所述,,本文對(duì)失步點(diǎn)d的估計(jì)方法為:
的譜范數(shù)來尋找信息碼的起點(diǎn)。顯然,,當(dāng)移動(dòng)分析窗使得信號(hào)達(dá)到同步時(shí),,其自相關(guān)矩陣的譜范數(shù)也會(huì)達(dá)到最大。綜上所述,,本文對(duì)失步點(diǎn)d的估計(jì)方法為:

如果事先得到的是信碼寬度的粗糙估計(jì)值,,本算法在以該粗糙估計(jì)值為中心的某一鄰域內(nèi)還可進(jìn)一步對(duì)失步點(diǎn)進(jìn)行精確估計(jì),此處不再詳述,,由計(jì)算機(jī)仿真可以得到驗(yàn)證,。
3 仿真實(shí)驗(yàn)
為了驗(yàn)證算法的有效性,本文利用MATLAB軟件進(jìn)行計(jì)算機(jī)仿真。采用31位m序列作為PN碼序列,,信噪比SNR=-10 dB,。假設(shè)采樣頻率為1 MHz,即Te=1 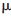 s,,且每個(gè)PN碼碼片含有2個(gè)采樣點(diǎn):Te=Tc/2,,失步時(shí)間t0=23Te。
s,,且每個(gè)PN碼碼片含有2個(gè)采樣點(diǎn):Te=Tc/2,,失步時(shí)間t0=23Te。
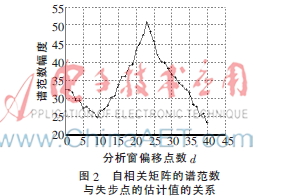
圖2給出了該信號(hào)分析窗內(nèi)數(shù)據(jù)的自相關(guān)矩陣的譜范數(shù)與分析窗偏移點(diǎn)數(shù)的關(guān)系,,從圖中可見當(dāng)分析窗偏移點(diǎn)數(shù)為23時(shí),,譜范數(shù)取得最大值,因此失步點(diǎn)的估計(jì)值為23,。
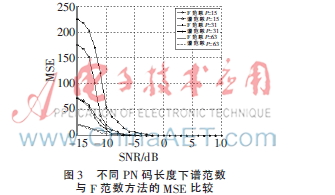
圖3針對(duì)不同PN碼長(zhǎng)的信號(hào),,給出了其譜范數(shù)與Frobenius范數(shù)的最小均方誤差(MSE)隨信噪比變化的情況??梢钥闯?,在同樣的碼長(zhǎng)與信噪比下,本文方法比Frobenius范數(shù)誤差小,,并且PN碼越長(zhǎng)優(yōu)勢(shì)越明顯,,這也驗(yàn)證了本文的理論分析。
4 結(jié)論
本文主要討論了DS-SS信號(hào)的盲同步問題,。由理論分析及計(jì)算機(jī)仿真可知,,本文提出的盲同步算法在低信噪比情況下,可以有效地實(shí)現(xiàn)DS-SS信號(hào)的盲同步,,并可在此基礎(chǔ)上估計(jì)出信號(hào)的其他參數(shù),。相比于已有的算法,該算法簡(jiǎn)單,、誤差小,,低信噪比下性能更優(yōu)越,不足之處在于求最大特征值的運(yùn)算量較大,,這也是本文今后改進(jìn)的方向,。
參考文獻(xiàn)
[1] 王滿喜,李宏,,馬刈非,,等.非周期性DSSS信號(hào)的PN碼序列盲估計(jì)[J].信號(hào)處理,2009,,25(10):1605-1611.
[2] 詹亞峰,,曹志剛,馬正新.DSSS信號(hào)的擴(kuò)頻序列估計(jì)[J].電子與信息學(xué)報(bào),,2005,,27(2):169-172.
[3] BOUDER C, AZOU S, BUREL G. A robust synchronization procedure for blind estimation of the symbol period and the timing offset in spread spectrum transmissions[C]. IEEE Seventh International Symposium on Spread Spectrum Techniques and Applications,, Prague,, 2002:238-241.
[4] BUREL G. Detection of spread spectrum transmissions using uctuations of correlation estimators[C]. IEEE Int. Symp. on Intelligent Signal Processing and Comm. Systems, Hawai,, 2000:5-8.
[5] 張?zhí)扃?,李立忠,張剛,,?直擴(kuò)信號(hào)的盲處理[M].北京:國(guó)防工業(yè)出版社,,2012.
[6] 陳景良,陳向輝.特殊矩陣[M].北京:清華大學(xué)出版社,,2001.

