摘  要： 針對(duì)雷達(dá)的目標(biāo)檢測(cè)概率和跟蹤精度隨著目標(biāo)距離的增大而降低的問題,，提出了一種基于門限體積最小準(zhǔn)則的認(rèn)知雷達(dá)的波形選擇方法,。該方法在高斯噪聲、線性運(yùn)動(dòng)目標(biāo)跟蹤方法的基礎(chǔ)上,，通過測(cè)量噪聲與發(fā)射波形之間的關(guān)系,，在經(jīng)典卡爾曼濾波算法的框架中增加了波形選擇模塊，來實(shí)現(xiàn)對(duì)跟蹤波形的調(diào)節(jié),。仿真結(jié)果表明,，該方法能夠明顯地提高雷達(dá)的跟蹤性能。

　　關(guān)鍵詞： 認(rèn)知雷達(dá),；卡爾曼濾波,；門限體積最小準(zhǔn)則

0 引言

　　隨著社會(huì)與科技的快速發(fā)展，無論是航?；蚴呛娇?，交通愈加繁忙。為了避免海上或是空中交通事故,，更早,、更準(zhǔn)確地發(fā)現(xiàn)對(duì)方船只或飛機(jī)，人們對(duì)于雷達(dá)的檢測(cè)能力和檢測(cè)精度有了更高的要求,。但只能發(fā)射固定波形的傳統(tǒng)雷達(dá),，由于探測(cè)目標(biāo)所處環(huán)境的復(fù)雜性，很難滿足現(xiàn)代人們的需求,。于是,，2006年，加拿大麥克馬斯特大學(xué)（McMaster University）國(guó)際著名信號(hào)處理專家Simon Haykin教授第一次提出了認(rèn)知雷達(dá)的概念[1],，并對(duì)認(rèn)知雷達(dá)的功能及各個(gè)組成部分做了詳細(xì)說明,。認(rèn)知雷達(dá)能夠通過對(duì)環(huán)境和目標(biāo)的特征進(jìn)行分析,，從而對(duì)信號(hào)智能處理，根據(jù)探測(cè)目的選擇相應(yīng)的發(fā)射波形,，提高雷達(dá)的檢測(cè)能力和精度,。Guerci[2]和Wicks[3]也分別在2010年IEEE國(guó)際雷達(dá)會(huì)議和認(rèn)知雷達(dá)信號(hào)處理國(guó)際研討會(huì)上從不同角度闡釋對(duì)認(rèn)知雷達(dá)的看法及其所需的相關(guān)技術(shù)。

　　對(duì)于雷達(dá)波形選擇技術(shù)的研究,，Kershaw和Evans[4]于1994年首次在傳統(tǒng)的雷達(dá)目標(biāo)跟蹤系統(tǒng)中增加了波形自適應(yīng)選擇模塊,。他們?cè)诼晠认到y(tǒng)中將發(fā)射波形參數(shù)引進(jìn)測(cè)量噪聲協(xié)方差，從而建立了發(fā)射波形與跟蹤算法之間的關(guān)系,，通過計(jì)算最小化估計(jì)誤差來得到最優(yōu)波形選擇方法,。Simon Haykin于2010年進(jìn)一步提出了基于容積Kalman濾波[5]的認(rèn)知跟蹤雷達(dá)的概念，以及預(yù)測(cè)跟蹤誤差最小化的最優(yōu)波形選擇準(zhǔn)則[6],，在經(jīng)典彈道目標(biāo)跟蹤的仿真中,，論證了認(rèn)知跟蹤雷達(dá)相較于只能發(fā)射固定波形的傳統(tǒng)雷達(dá)的優(yōu)勢(shì)。東北大學(xué)的王彬[7]針對(duì)雷達(dá)目標(biāo)轉(zhuǎn)移概率未知的特點(diǎn),，把自適應(yīng)波形選擇問題建模為隨機(jī)動(dòng)態(tài)規(guī)劃模型,，提出應(yīng)用Q學(xué)習(xí)的方法進(jìn)行波形選擇。北京裝備學(xué)院的俞道濱[8]在基于波形庫(kù)的目標(biāo)跟蹤波形選擇方法上也做了論證,，得出了不同的波形選擇準(zhǔn)則能夠根據(jù)需求提高雷達(dá)跟蹤的精確度和準(zhǔn)確性的結(jié)論,。

1 認(rèn)知雷達(dá)波形選擇的系統(tǒng)框圖

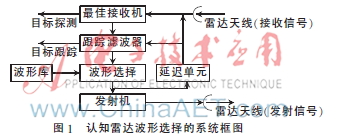
　　認(rèn)知雷達(dá)波形選擇的系統(tǒng)框圖如圖1所示。在傳統(tǒng)的雷達(dá)目標(biāo)探測(cè)及跟蹤過程中,，沒有發(fā)射波形選擇的模塊,。波形選擇模塊通過預(yù)測(cè)協(xié)方差選擇下一時(shí)刻的發(fā)射波形，發(fā)射波形不同,，測(cè)量噪聲方差的Cramer-Rao下限（CRLB）也不同,，從而對(duì)測(cè)量方程產(chǎn)生影響[9]。

　　2 信號(hào)模型

　　通常雷達(dá)發(fā)射的波形sT（t）為[1]：

　　式（3）中,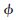，為隨機(jī)相移,，ER為接收信號(hào)的能量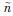，（t）為零均值的高斯白噪聲,，它的頻譜密度為N0/2,，參數(shù)τ0和v0分別為目標(biāo)的時(shí)延和Doppler頻移。在對(duì)運(yùn)動(dòng)目標(biāo)進(jìn)行跟蹤時(shí),，通過對(duì)發(fā)射和接收信號(hào)的分析,，可以實(shí)時(shí)獲取目標(biāo)的距離和速度等信息。

3 跟蹤濾波算法

　　本文提出的目標(biāo)模型是在無雜波,、高斯噪聲環(huán)境中做線性運(yùn)動(dòng)的條件下的構(gòu)造,。在此情況下，卡爾曼濾波就是最優(yōu)的貝葉斯濾波器[10]。

　　設(shè)專為波形參數(shù)的可選集合,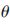，k為k時(shí)刻的發(fā)射波形,，則測(cè)量噪聲協(xié)方差為N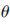（k），由卡爾曼濾波可知,，測(cè)量信息協(xié)方差為：

　　在已知目標(biāo)的初始狀態(tài)及其運(yùn)動(dòng)模型等條件時(shí),，經(jīng)以上幾個(gè)方程式交替循環(huán)計(jì)算，可獲得目標(biāo)狀態(tài)和量測(cè)的更新值,，實(shí)現(xiàn)對(duì)目標(biāo)的跟蹤,。

4 波形選擇準(zhǔn)則及最優(yōu)化方案

　　波形選擇準(zhǔn)則是下一時(shí)刻發(fā)射什么樣的波形的依據(jù)，它與跟蹤的目的緊密相關(guān),，不同的跟蹤目的將有不同的波形選擇準(zhǔn)則,。本文從使跟蹤k時(shí)刻測(cè)量空間的體積最小，減少在高密度雜波下的虛假測(cè)量數(shù)或者高噪聲情況下的測(cè)量誤差的角度考量,，采用門限體積最小準(zhǔn)則,。其表達(dá)式為：

　　式（10）在參考文獻(xiàn)[2]中有詳細(xì)的推導(dǎo)過程,。

　　波形最優(yōu)化方案則是下一時(shí)刻選擇發(fā)射波形的方式,。波形最優(yōu)化方案主要包括波形設(shè)計(jì)和波形選擇。波形設(shè)計(jì)主要是利用動(dòng)態(tài)變化環(huán)境來設(shè)計(jì)波形,，其主要缺點(diǎn)是實(shí)時(shí)性較差,，因而在雷達(dá)中幾乎很少采用。波形選擇則需在雷達(dá)工作前設(shè)計(jì)好一組波形或波形參數(shù),，建立波形庫(kù),。雷達(dá)工作時(shí)，根據(jù)波形選擇準(zhǔn)則在波形庫(kù)內(nèi)選擇最優(yōu)的波形,。隨著大容量存儲(chǔ)器及高速率處理器的發(fā)展,，波形選擇具有更高的可實(shí)現(xiàn)性，故本文波形最優(yōu)化方案采用的是波形選擇,。如圖2所示,，一般波形庫(kù)會(huì)采用多種不同的波形。而本文只采用3種典型的雷達(dá)信號(hào)波形,，在跟蹤不同距離,、不同速度的目標(biāo)時(shí)具有各自的特點(diǎn)。根據(jù)雷達(dá)性能的需求,，調(diào)用最優(yōu)的波形,。

5 仿真實(shí)驗(yàn)及結(jié)果分析

　　本文仿真實(shí)驗(yàn)中采用的三種信號(hào)波形的函數(shù)表達(dá)式分別為：

　　三角脈沖信號(hào)：

　　三角脈沖信號(hào)的有效脈沖寬度為2λ，高斯調(diào)制脈沖信號(hào)和高斯調(diào)制線性調(diào)頻信號(hào)的脈沖寬度為7.433 8λ,。對(duì)于三角脈沖信號(hào)和高斯調(diào)制脈沖信號(hào)只能進(jìn)行脈寬調(diào)制,，而對(duì)高斯調(diào)制線性調(diào)頻信號(hào)的脈寬和調(diào)頻率都可調(diào)制。

　　仿真實(shí)驗(yàn)的環(huán)境相關(guān)參數(shù)及目標(biāo)的初始狀態(tài)：

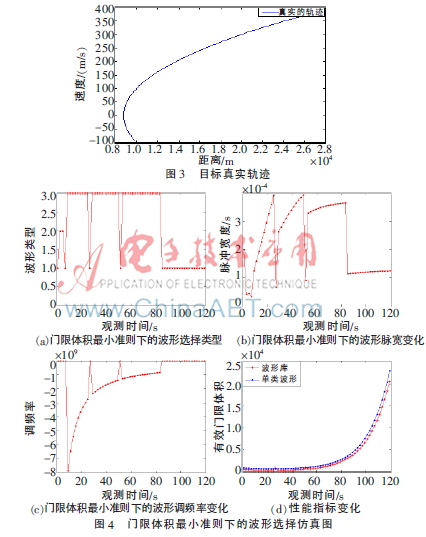
　　假設(shè)使用一座距離-速度同時(shí)觀測(cè)的雷達(dá)平臺(tái)對(duì)一目標(biāo)進(jìn)行觀測(cè)跟蹤,，此目標(biāo)先靠近該平臺(tái)運(yùn)動(dòng)再遠(yuǎn)離該平臺(tái)運(yùn)動(dòng),。設(shè)遠(yuǎn)離平臺(tái)方向?yàn)檎?，靠近平臺(tái)方向?yàn)樨?fù)。如圖3所示為目標(biāo)的距離和速度軌跡,。該目標(biāo)初始距離r為10 000 m,，速度為-100 m/s，加速度為4 m/s2,。觀測(cè)值為距離和速度,，觀測(cè)間隔t=2 s，觀測(cè)時(shí)長(zhǎng)120 s,。雷達(dá)跟蹤系統(tǒng)模型中的參數(shù)為：

　　目標(biāo)跟蹤的初始協(xié)方差矩陣為：

　　過程噪聲方差Q=0.000 1,。設(shè)雷達(dá)的有效觀測(cè)距離為200 km，則信噪比可以表示為：

　　SNR=（200 000/s）4（14）

　　式中,，s表示目標(biāo)到雷達(dá)的距離,。初始波形選為三角脈沖，其初始脈沖寬度為λ=100 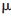s,，脈沖寬度參數(shù)變化范圍為30~400 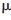s,，調(diào)頻參數(shù)b變化范圍為-10×109~10×109。與之相對(duì)比的傳統(tǒng)雷達(dá),，采用高斯調(diào)制調(diào)頻單類波形,。其固定發(fā)射脈寬λ=5×10-7 s，調(diào)頻參數(shù)b=5×109,。在門限體積最小準(zhǔn)則下,，經(jīng)過500次蒙特卡羅仿真運(yùn)算，得到其仿真結(jié)果如圖4所示,。

　　由仿真結(jié)果圖4可知,，在跟蹤目標(biāo)距離雷達(dá)觀測(cè)平臺(tái)較近時(shí)，認(rèn)知雷達(dá)根據(jù)門限體積最小準(zhǔn)則選用的是高斯調(diào)制線性調(diào)頻信號(hào),，使跟蹤目標(biāo)的門限體積保持在較小的范圍內(nèi),。在跟蹤過程中，調(diào)頻率逐漸增大,，以保持在跟蹤過程中測(cè)量空間的體積較小,。而在跟蹤目標(biāo)距離雷達(dá)觀測(cè)平臺(tái)較遠(yuǎn)時(shí)，認(rèn)知雷達(dá)選用的是三角脈沖,，使跟蹤目標(biāo)的門限體積明顯小于無波形庫(kù)的情況,，能夠有效地提高雷達(dá)遠(yuǎn)距離的探測(cè)精度。其中的波形脈沖脈寬變化和調(diào)頻率圖像的陡然落差,，主要是由于波形庫(kù)中波形的脈寬限制所造成的,。

6 結(jié)束語

　　本文研究了與傳統(tǒng)跟蹤雷達(dá)相比能夠自適應(yīng)選擇發(fā)射波形的認(rèn)知雷達(dá)，其在無雜波、高斯白噪聲及跟蹤目標(biāo)做線性運(yùn)動(dòng)的情況下,，根據(jù)門限體積最小準(zhǔn)則從建立的波形庫(kù)中選擇最優(yōu)發(fā)射波形,。通過與傳統(tǒng)跟蹤雷達(dá)對(duì)比可知，認(rèn)知雷達(dá)的跟蹤性能的確得到了顯著提升,。

　　參考文獻(xiàn)

　　[1] HAYKIN S． Cognitive radar： a way of the future[J]. IEEE Signal Processing Magazine,，2006，23（1）：30-40.

　　[2] GUERCI J R.Cognitive radar： a knowledge-aided fully adaptive approach[C]． Processings of IEEE Radar Conference,， Washington DC,， IEEE Press，2010：1365-1370.

　　[3] WICKS M． Spectrum crowding and cognitive radar[C]． 2nd International Workshop on Cognitive Information Processing,，IEEE Press,，2010：452-457.

　　[4] KERSHAW D J，EVANS R J． Optimal waveform selection for tracking systems[J]． IEEE Transactions on Information Theory,， 1994,，40（5）：1536-1550．

　　[5] ARASARATNAM I ， HAYKIN S. Cubature Kalman filters[C]. IEEE Transaction on Automatic Control,， 2010：1254-1269.

　　[6] HAYKIN S. Cognitive tracking radar[C]. IEEE Radar Conference,， 2010：1467-1470.

　　[7] 王彬，汪晉寬,，宋昕．認(rèn)知雷達(dá)中基于Q學(xué)習(xí)的自適應(yīng)波形選擇算法[J]．系統(tǒng)工程與電子技術(shù),，2011,，33（5）：1007-1011．

　　[8] 俞道濱,，吳彥鴻，朱衛(wèi)綱．基于波形庫(kù)的目標(biāo)跟蹤波形選擇方法研究[J]．雷達(dá)與對(duì)抗,，2013,，33（2）：35-39．

　　[9] 夏洪恩．基于目標(biāo)跟蹤的波形自適應(yīng)選擇技術(shù)[D]．長(zhǎng)沙：國(guó)防科技大學(xué)，2010．

　　[10] 何友,，修建娟,，關(guān)欣，等．雷達(dá)數(shù)據(jù)處理及應(yīng)用（第三版）[M]．北京：電子工業(yè)出版社,，2013．