文獻標識碼： A
DOI：10.16157/j.issn.0258-7998.2016.02.003
中文引用格式： 賀江,，蒲宇亮,，李海波，等. 一種基于OpenCL的高能效并行KNN算法及其GPU驗證[J].電子技術應用,，2016,，42(2)：14-16.
英文引用格式： He Jiang，Pu Yuliang,，Li Haibo,，et al. A energy efficient parallel KNN algorithm evaluated on GPU using OpenCL[J].Application of Electronic Technique,，2016，42(2)：14-16.
0 引言
近年來,，許多不同類型的處理器廣泛應用于高性能計算領域,，如GPU,、FPGA,、DSP等[1]，而異構計算平臺由不同類型的處理器組成,，能對許多不同的算法進行加速實現(xiàn),。OpenCL是一種開放式的異構計算標準，支持異構系統(tǒng)的并行程序應用,。作為經(jīng)典聚類算法,，KNN在文字識別、預測分析,、圖像處理和圖像識別等方面[2]有非常重要的應用,。
為了加速KNN算法的實現(xiàn)，許多文章也提出了一些新的思路,。Zhang Hao等[3]通過結合支持向量機(SVM)和KNN算法實現(xiàn)視覺分類識別,。Garcia等[4]提出一種基于插入排序的快速KNN算法實現(xiàn)，并分析了奇偶排序和插入排序的性能,。2009年,，Liang Shenshen等人[5]提出了基于CUDA實現(xiàn)的并行KNN算法，稱該算法為CUKNN,。該算法通過調用大量GPU線程,，在計算待分類數(shù)據(jù)和參考數(shù)據(jù)集時高度并化，然后對距離進行并行排序,。
基于CPU+GPU的異構計算系統(tǒng)最近幾年在算法加速方面得到了廣泛使用,，如神經(jīng)網(wǎng)絡[6],、數(shù)據(jù)挖掘[7]等。而基于CPU+FPGA系統(tǒng)由于其能效優(yōu)勢[8],，得到業(yè)界的認可,。
本文提出了一種基于CPU+GPU異構計算系統(tǒng)的KNN并行算法。該方法將待分類的數(shù)據(jù)集通過并行冒泡的方法進行分類,，稱該方法為PBKNN（parallel sort）,。
1 KNN算法與OpenCL架構
1.1 KNN算法
KNN分類算法實現(xiàn)簡單，分類錯誤率低,，其實現(xiàn)通常分為三步：距離計算,、距離排序、分類判決,。
距離計算是計算待分類數(shù)據(jù)和參考數(shù)據(jù)集數(shù)據(jù)之間的距離,，本文采用的是歐式距離。
算出待分類數(shù)據(jù)與每個參考數(shù)據(jù)集樣本之間的距離之后,，需選出其中最小的K個距離,，作為判決的標準。針對如何從多個數(shù)據(jù)中選取K個最小的數(shù)據(jù),，提出了一種新的并行冒泡排序方法,，該方法無冗余計算且可并行實現(xiàn)。并行冒泡排序也曾被提出來加速排序的計算速度,，如奇偶冒泡排序[9],，但該算法由于大量冗余計算，實現(xiàn)時性能不佳,。本文提出的并行冒泡排序只需要K個氣泡來選取K個最小的數(shù)據(jù),，如圖1所示。
1.2 OpenCL架構
OpenCL程序在主機和設備上執(zhí)行,，支持基于數(shù)據(jù)和基于任務的并行編程模型,。圖2是有主機的多個設備組成的OpenCL平臺模型[10]。
執(zhí)行內核程序時,，OpenCL將定義一個索引來執(zhí)行該內核的實例,，該實例就是OpenCL的工作項，每個工作項執(zhí)行的代碼相同,。工作項的內存稱作私有內存,。一些特定的工作項組成工作組，相同工作組共享局部內存,，相同工作組中的不同工作項在不同計算單元上并行運行,。
本文采用通用圖形處理器（GPGPU）來作為異構系統(tǒng)的計算設備，由于GPU擁有大量的計算核心,，其浮點計算效率遠高于CPU,，所以GPU作為OpenCL的通用計算設備擁有很高的計算效率,。
2 并行冒泡的KNN算法實現(xiàn)
2.1 距離計算內核
距離計算內核計算每個待分類數(shù)據(jù)到每個參考數(shù)據(jù)集樣本之間的距離，每次距離計算由一個工作項完成,。數(shù)據(jù)集由CPU傳輸?shù)紾PU的全局內存,，相應工作組的數(shù)據(jù)由GPU全局內存?zhèn)鬏數(shù)紾PU局部內存，以此充分利用局部內存的帶寬,，提高GPU計算核心的數(shù)據(jù)訪存速度,。距離計算如圖3所示。
2.2 距離分組排序內核
為了充分利用GPU的計算資源,，提高計算的并行度,，將得到的待分類數(shù)據(jù)和參考數(shù)據(jù)集的所有距離進行排序時，先將距離分組,，若分組數(shù)為N,，通過并行冒泡選取每組數(shù)據(jù)最小的K個距離，得到N×K個距離,。一個待分類數(shù)據(jù)共有N個工作組進行分組排序,。
每個工作組通過并行冒泡進行排序，一個工作組擁有K個工作項,，每個工作項對比相鄰的兩個數(shù)據(jù),，K個工作項從數(shù)據(jù)的起始端一直對比到數(shù)據(jù)的末端，從而選出最小的K個距離,。第1個周期時,，共一個工作項進行第1個和第2個距離進行比較；第2個周期時,，第1個氣泡比較第3個和第4個距離，第2個數(shù)據(jù)比較第1個和第2個距離,，直到N個工作項產(chǎn)生N個氣泡,。氣泡數(shù)目穩(wěn)定后，經(jīng)過若干個周期,，K個氣泡便可以同時攜帶K個最小的距離,。所以該過程共有2個過程，氣泡增加,，氣泡穩(wěn)定,。具體過程如圖4、圖5所示,。
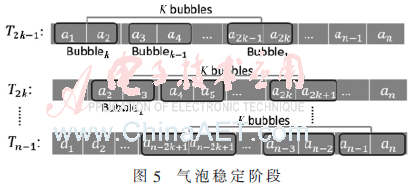
2.3 距離計算內核
在分組內核中,，每個待分類數(shù)據(jù)共得到M×K個距離，該內核就是從這M×K個數(shù)據(jù)中選出K個最小的數(shù)據(jù),。由于參考數(shù)據(jù)集很大,，這個內核消耗的計算時間相比分組排序只占小部分,。
3 結果分析
3.1 算法性能分析
為了讓距離分組內核得到合理的分組數(shù)目，通過設置不同的分組數(shù)目,，得到在GPU上計算消耗的時間,。實驗中，采用英特爾處理器i7-3770K作為OpenCL主機,，AMD Radeon HD7950作為OpenCL設備,。該CPU是4核處理器，主頻3.5 GHz,，24 GB內存,。該GPU擁有28個計算單元，最大工作頻率為900 MHz,，3 GB GDDR5內存,，內存帶寬為240 GB/s。所有實驗數(shù)據(jù)由MATLAB產(chǎn)生,，參考數(shù)據(jù)集為10 240×8個浮點數(shù)據(jù),，每個數(shù)據(jù)共64維，K為16,，待分類數(shù)據(jù)個數(shù)為32,。
為了找到每個待分類數(shù)據(jù)距離的最佳分組數(shù)，將每個待分類數(shù)據(jù)10 240×8個參考數(shù)據(jù)集的距離進行分組,，將分組數(shù)分別設置為4×8,，8×8，直至48×8,。通過實驗,，記錄每次實驗的GPU時間消耗，如圖6所示,。
當分組數(shù)較小時,，分組排序內核隨著分組數(shù)的變大，時間消耗迅速下降,；當分組數(shù)變大后,，時間消耗趨于穩(wěn)定。因為當分組數(shù)較小時,，每個工作項的計算量和數(shù)據(jù)傳輸量過大,，且GPU的計算資源沒有充分利用；當分組數(shù)變大后,，GPU計算資源得到充分利用,，但工作組和工作項的數(shù)目也會隨之變大，從而導致額外的控制開銷,。根據(jù)實驗數(shù)據(jù),，將分組數(shù)設定為32,。
本次實驗，把CUKNN和PBKNN進行OpenCL實現(xiàn)時,，工作組大小均設置為256,。CUKNN進行排序時，每個工作組將浪費(256-K)/256×100%的時間計算無關數(shù)據(jù)的排序,。而PBKNN對此進行優(yōu)化,，避免了無關數(shù)據(jù)的排序。所以,，理論上來說,，PBKNN的時間消耗是CUKNN的K/256。
3.2 實驗驗證
PBKNN和CUKNN采用相同的數(shù)據(jù)和相同的實驗環(huán)境,。參考數(shù)據(jù)集中數(shù)據(jù)點個數(shù)從1×10 240到64×10 240變化,，如表1。對于PBKNN,，共有256個工作組,，每個工作組共有64個工作項；對于CUKNN,，工作組數(shù)目分別設置為40,，80，120,，…,，320，其每個工作組的工作項數(shù)目最大時,，性能最好,。所以每個工作組的工作項的數(shù)目設置為256。
BPKNN和CUKNN均通過三個內核實現(xiàn)KNN算法,。由于第一個和第三個內核的時間消耗較少,，主要對比第二個內核的時間消耗。實驗結果如表1,。
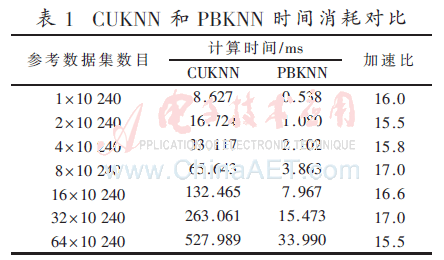
從實驗結果可以看出，在相同的實現(xiàn)平臺上通過減少無關數(shù)據(jù)的排序,，PBKNN相比于CUKNN計算時間大幅減少,，因而對應的能量效率也得到了很大的提升,。
4 結論
本文提出了一種基于CPU+GPU的異構計算架構的并行冒泡KNN算法—PBKNN算法,，該算法充分利用了GPU的并行計算能力及OpenCL的編程優(yōu)化。通過在AMD Radeon HD GPU實測,，PBKNN在關鍵排序時間僅為CUKNN的1/16,，因而極大地提升了處理速度和計算能效,。
參考文獻
[1] Khronos group.The open standard for parallel programming of heterogeneous systems[EB/OL].http：//www.khronos.org/opencl/.
[2] PENG Y,，KOU G，SHI Y,，et al.A descriptive framework for the field of data mining and knowledge discovery[J].Int.J.Inf.Technol.Decis.Mak.,，2008，7(4)：639-682.
[3] ZHANG H,，BERG A C,，MAIRE M，et al.SVM-KNN：discriminative nearest neighbor classification for visual category recognition[C].In International Conference on Computer Vision and Pattern Recognition,，New York(NY),，USA，2006.
[4] GARCIA V,，DEBREUVE E,，BARLAUD M.Fast k nearest neighbor search using GPU[C].In：IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops(CVPRW′08)，2008：1-6.
[5] LIANG S,，WANG C,，LIU Y，et al.CUKNN：a parallel implementation of knearest neighbor on cuda enabled GPU[C].In：IEEE Youth Conference on Information,，Computing and Telecommunication(YC-ICT′09),，2009：415-418.
[6] HOFFMANN J，EI-LAITHY K,，G?譈TTLER F,，et al.Simulating biological-inspired spiking neural networks with OpenCL[C].ICANN 2010，Part I,，LNCS 6352,，2010：184-187.
[7] CHE S，BOYER M,，MENG J Y,，et al.A performance study of general purpose applications on graphics processors[J].Journal of Parallel and Distributed Computing，2008,，68(10)：137-1380.
[8] BALEVIC A,，ROCKSTROH L，LI W,，et al.Acceleration of a finite-difference time-domain method with general purpose GPUs(GPGPUs)[C].Proc.of International Conference on Computer and Information Technology,，2008，1-2：291-294.
[9] PETERS H,，SCHULZ-HILDEBRANDT O,，LUTTENBERGER N.A novel sorting algorithm for many-core architectures based on adaptive bitonic sort[C].In：Parallel & Distributed Processing Symposium(IPDPS)，2012 IEEE 26th International，2012.
[10] GROUP K O W.The opencl specification[EB/OL].(2011)[2015].http：//www.khronos.org/registry/cl/specs/opencl-1.1.pdf.