葛欣星,， 程劍， 梁凝睿

（中國(guó)人民解放軍理工大學(xué) 通信工程學(xué)院,，江蘇 南京 210000）

　　摘要：為了消除直接擴(kuò)頻通信系統(tǒng)中寬帶干擾信號(hào),，極性消除（Polar Exciser）算法被提出，其實(shí)質(zhì)是極性轉(zhuǎn)換和變換域陷波濾波的結(jié)合,。但其在干擾功率較低時(shí)，系統(tǒng)性能急劇下降,。本文提出了一種基于極性消除算法的改進(jìn)算法,，用以消除不同類(lèi)型的寬帶恒包絡(luò)干擾信號(hào)。本文通過(guò)引入變異系數(shù)來(lái)選擇使用極性消除干擾抑制器還是匹配濾波器,。對(duì)通過(guò)改進(jìn)后的極性消除算法來(lái)抑制寬帶恒包絡(luò)干擾信號(hào)后的誤碼率進(jìn)行仿真,，結(jié)果表明了該改進(jìn)算法對(duì)寬帶恒包絡(luò)的干擾信號(hào)有著較好的抑制作用，且變異系數(shù)是一種有效的切換策略,。

　　關(guān)鍵詞：極性消除,；掃頻,；線性調(diào)頻；變異系數(shù),；誤碼率

0引言

　　擴(kuò)展頻譜通信是指用來(lái)傳輸信息所用的信號(hào)帶寬遠(yuǎn)大于信息本身帶寬的一種通信方式,。擴(kuò)頻通信技術(shù)具有很多優(yōu)點(diǎn)：抗干擾、抗噪聲,、抗多徑衰落,、具有保密性、功率譜密度低,、具有隱蔽性和低截獲率,，可多址復(fù)用和任意選址等。直接序列擴(kuò)頻（Direct Sequence Spread Spectrum, DSSS）作為一種有效的抗干擾通信體制,，在移動(dòng)通信和軍事通信中得到廣泛的應(yīng)用,。擴(kuò)頻系統(tǒng)的抗干擾能力由干擾容限決定，而干擾容限取決于系統(tǒng)的擴(kuò)頻增益,。然而受到頻譜資源的限制,，擴(kuò)頻增益不能無(wú)限制提高，當(dāng)干擾的功率超過(guò)擴(kuò)頻通信的抗干擾容限時(shí),，擴(kuò)頻增益不足以保證對(duì)有用信號(hào)的可靠譯碼,，通信性能將會(huì)急劇下降。這時(shí),，必須引入相應(yīng)的抗干擾技術(shù)來(lái)消除干擾信號(hào)?，F(xiàn)有研究對(duì)窄帶干擾的抑制技術(shù)相對(duì)成熟，而對(duì)干擾信號(hào)帶寬占有用信號(hào)帶寬20%以上即寬帶干擾的研究起步較晚［13］,。而隨著信號(hào)傳輸速率越來(lái)越快,，信號(hào)帶寬也越來(lái)越寬，因此衛(wèi)星通信中寬帶干擾信號(hào)對(duì)系統(tǒng)通信質(zhì)量的影響越來(lái)越受到人們的重視,。

　　在面對(duì)寬帶干擾時(shí),，現(xiàn)有的研究只有為數(shù)不多的幾種方法可用來(lái)進(jìn)行干擾消除，比如時(shí)變自適應(yīng)濾波器（TDAF）,。但由于TDAF利用了循環(huán)平穩(wěn)特性,，該算法需要知道接收信號(hào)的準(zhǔn)確的循環(huán)頻率的先驗(yàn)條件，因此其計(jì)算復(fù)雜度特別高,，并且收斂速度也非常慢,。本文提出了一種用來(lái)抑制恒包絡(luò)的寬帶干擾信號(hào)的極性消除（Polar Exciser, PE）算法［4］。由于不需要對(duì)接收信號(hào)參數(shù)進(jìn)行估計(jì),，所以該方法計(jì)算復(fù)雜度較低,，且其性能穩(wěn)定并不需要收斂時(shí)間。仿真結(jié)果表明極性消除干擾抑制器可以有效抑制包絡(luò)幅度相同的寬帶干擾信號(hào)，但存在的缺點(diǎn)是當(dāng)干擾功率較小時(shí)其性能急劇下降,。為了解決PE算法在干擾功率較小時(shí)性能急劇下降的問(wèn)題,，提出了一種改進(jìn)算法，通過(guò)變異系數(shù)的選擇［5］使得PE干擾抑制器只在干擾功率達(dá)到一定值后工作,，在一定程度上提高了系統(tǒng)的性能,。

1極性消除算法

　　1.1直接擴(kuò)頻系統(tǒng)

　　為了得到較高的處理增益，直接序列擴(kuò)展一般直接通過(guò)傳輸通道,，數(shù)據(jù)序列通過(guò)與由PN碼發(fā)生器產(chǎn)生的直接序列擴(kuò)頻碼字相乘進(jìn)行調(diào)制,。在本文的系統(tǒng)場(chǎng)景中，假設(shè)信道是簡(jiǎn)單的加性高斯白噪聲信道,，且寬帶干擾信號(hào)是恒包絡(luò)的,，信道是單路的即沒(méi)有符號(hào)間串?dāng)_，其相位誤差為0,。在接收端,，信號(hào)進(jìn)入PE干擾抑制器中，然后信號(hào)通過(guò)與擴(kuò)頻碼字匹配的濾波器進(jìn)行擴(kuò)頻解調(diào),。圖1直擴(kuò)系統(tǒng)的干擾抑制算法的系統(tǒng)框圖

　　直接序列擴(kuò)頻系統(tǒng)的干擾抑制系統(tǒng)框圖如圖1所示,。

　　1.2極性消除算法

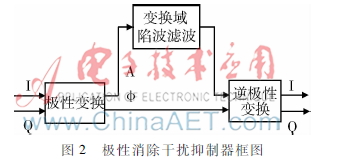
　　極性消除算法本質(zhì)上是極性轉(zhuǎn)換和變換域陷波濾波的結(jié)合，其系統(tǒng)框圖如圖2所示,。在PE算法中,，首先對(duì)接收信號(hào)進(jìn)行采樣，而后轉(zhuǎn)化為基帶信號(hào),，接著采樣后的接收信號(hào)被極性轉(zhuǎn)化為幅度和相位序列,。幅度序列直接通過(guò)FFT陷波濾波器將代表干擾的最大分量從序列中濾除。此后,，干擾抑制后的接收信號(hào)通過(guò)利用陷波后的幅度序列和原始相位序列構(gòu)成的逆極性變化回時(shí)域,。

　　假設(shè)在干擾抑制器輸入端有K bit間隔的接收信號(hào)：

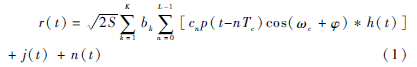
　　其中，p(t)是陷波波形（矩形）,，h(t)是信道脈沖響應(yīng),，j(t)代表干擾信號(hào)，n(t)是高斯白背景噪聲,，L是直接序列碼長(zhǎng),，而cn∈［-1,1］是碼序列的第k個(gè)元素。

　　極性消除算法的計(jì)算步驟主要由以下幾個(gè)部分組成：在極性轉(zhuǎn)換中,，接收到的采樣后信號(hào)r(n)被轉(zhuǎn)換成幅度m序列和相位φ序列,，如下式：

　　幅度序列的DFT變換可以用下式計(jì)算：

　　其中，NDFT是DFT變換的長(zhǎng)度,。

　　變換后，幅度頻譜Λ可表示為：

　　幅度頻譜Λ的均值為：

　　接著，通過(guò)由mexc和φ組成的逆極性變換產(chǎn)生干擾抑制后的接收信號(hào)：

　　rs(k)=mexc(k)ejφ(k)（8）

　　抑制后的接收信號(hào)進(jìn)入匹配濾波器后輸出信號(hào),。

　　1.3干擾信號(hào)

　　干擾信號(hào)j(t)可表示為：

　　式中Δω是干擾信號(hào)頻率到擴(kuò)頻信號(hào)中心頻率ωc的頻偏,，θi是干擾信號(hào)的初始相位，干擾信號(hào)的符號(hào)ak∈［－1, 1］,，q(t)是干擾信號(hào)的比特波形,。

　　掃頻干擾信號(hào)可表示為：

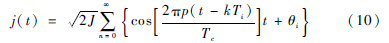
　　式中Tc為擴(kuò)頻信號(hào)的碼片時(shí)間，是干擾信號(hào)到擴(kuò)頻信號(hào)中心頻率的頻偏,，一個(gè)符號(hào)時(shí)間Ti內(nèi)干擾信號(hào)波形的頻率在有用擴(kuò)頻信號(hào)的帶寬上不斷變化,。

　　掃頻干擾信號(hào)的帶寬為：

　　式中,φ(t,θk)=2πfkt+πg(shù)kt2，而θk=(fk,gk),，fk代表信號(hào)的初始頻率,，gk是頻率的變化率。

2改進(jìn)策略

　　變異系數(shù)（coefficient of variation）反映了變量與其均值之間的偏差,，因此也稱(chēng)之為相對(duì)標(biāo)準(zhǔn)偏差（relative standard deviation）,，其值與均值大小無(wú)關(guān)。變異系數(shù)越小說(shuō)明偏差越小,，反之亦然,。

　　變異系數(shù)可表示為：

　　其中，是指變量的標(biāo)準(zhǔn)差,，即方差的算術(shù)平方根,，而(·)代表了采樣均值。從上式可以看出,，變異系數(shù)實(shí)際上就是變量的標(biāo)準(zhǔn)差和均值的比值,。采樣信號(hào)可能是時(shí)域，也可能是其他變換域,，因此通過(guò)變異系數(shù)值的比較來(lái)確定最終選擇的變換域,。

　　變異系數(shù)首次被應(yīng)用于通信系統(tǒng)的抗干擾［6］，在文獻(xiàn)中通過(guò)壓縮干擾信號(hào)使之更容易被消除,。從變異系數(shù)的定義可以看出,，變異系數(shù)值越高，在變換域中有用信號(hào)的能量越集中在一個(gè)更小的范圍內(nèi),，這樣就越容易在不干擾有用信號(hào)的情況下消除干擾信號(hào),。因此，在時(shí)域和傅里葉域分別計(jì)算變異系數(shù)值ε,，時(shí)域中變異系數(shù)設(shè)為CV1而傅里葉域中為CV2,。變異系數(shù)CV值最大的變換域被認(rèn)為是最適合用于干擾抑制的變換域。從圖3可以看出變異系數(shù)隨著干信比增大的變化趨勢(shì),，CV1值越來(lái)越趨向于0,，而CV2值越來(lái)越接近1,；但當(dāng)干信比較小時(shí)，CV1和CV2波動(dòng)幅度相當(dāng),。因此需要通過(guò)一個(gè)預(yù)設(shè)定變量α調(diào)整變異系數(shù),，從而達(dá)到選擇變換域的效果?！?/p>

　　最終的切換策略：當(dāng)αεCV1>εCV2時(shí),，系統(tǒng)使用匹配濾波器；當(dāng)αεCV1≤εCV2時(shí),，使用極性消除算法,。

　　通過(guò)計(jì)算CV1和CV2進(jìn)行比較來(lái)選擇是否使用極性消除干擾抑制器，通過(guò)切換策略來(lái)改進(jìn)算法的系統(tǒng)框圖,，如圖4所示,。當(dāng)干擾功率較低時(shí)，該改進(jìn)算法不使用干擾抑制器而直接通過(guò)系統(tǒng)的匹配濾波器對(duì)干擾信號(hào)進(jìn)行抑制,；而當(dāng)干擾功率較高時(shí),，則使用極性消除干擾抑制器對(duì)干擾信號(hào)進(jìn)行抑制消除。

3仿真

　　3.1仿真系統(tǒng)

　　仿真系統(tǒng)假設(shè)是有PE干擾抑制器的DSSS系統(tǒng),，調(diào)制方式為BPSK,，干擾抑制是實(shí)時(shí)的，PE干擾抑制器的輸入信號(hào)由DSSS信號(hào),、高斯白噪聲和干擾組成,。經(jīng)PE干擾抑制器處理后的信號(hào)直接進(jìn)入與DS碼字匹配的濾波器，匹配濾波器是與接收信號(hào)完全同步的,。匹配濾波器的輸出進(jìn)入一個(gè)硬限幅器來(lái)產(chǎn)生比特判定以達(dá)到性能衡量的目的,。

　　假設(shè)仿真系統(tǒng)中PN碼是長(zhǎng)度為31的m序列，采樣間隔為4,，則一個(gè)比特的長(zhǎng)度就變成了124,，極性變換和FFT以及逆變換在每個(gè)循環(huán)模塊內(nèi)都要進(jìn)行計(jì)算。干擾信號(hào)是時(shí)變的,，且在一個(gè)循環(huán)內(nèi)干擾信號(hào)的功率是恒定的,。干擾信號(hào)的頻率到直擴(kuò)信號(hào)中心頻率的頻偏范圍為［0,0.5］，干擾信號(hào)的初始相位范圍為［0,2π］,，并且假定在信號(hào)傳輸過(guò)程中,，每個(gè)字節(jié)都被干擾了，一共仿真了100 000字節(jié),，干擾信號(hào)是帶寬和DS信號(hào)帶寬相同的恒包絡(luò)信號(hào),。

　　3.2仿真結(jié)果

　　隨著干信比的不斷增大，分別使用匹配濾波器和極性消除算法進(jìn)行誤碼率比較,，仿真結(jié)果如圖5和圖6所示,。在本次仿真環(huán)境中,，設(shè)信噪比為12 dB。圖5和圖6說(shuō)明了當(dāng)干信比小于13 dB時(shí),，匹配濾波器的誤碼率優(yōu)于極性消除干擾抑制器,，并且在干信比大于20 dB時(shí)誤碼率都會(huì)趨于穩(wěn)定。仿真結(jié)果表明,，當(dāng)干擾信號(hào)的包絡(luò)幅度相等時(shí)，恒包絡(luò)干擾信號(hào)的類(lèi)型對(duì)系統(tǒng)性能的影響不大,。當(dāng)干信比超過(guò)13 dB時(shí),，極性消除干擾抑制器的誤碼率更好，而當(dāng)干信比較低時(shí),，干擾抑制器的引入會(huì)使得誤碼率偏高,。因此需要加入一個(gè)切換算法使得在干信比較低的環(huán)境中，極性消除干擾抑制器不工作,。

　　在這種情況下,，引入了變異系數(shù)策略。變異系數(shù)通過(guò)

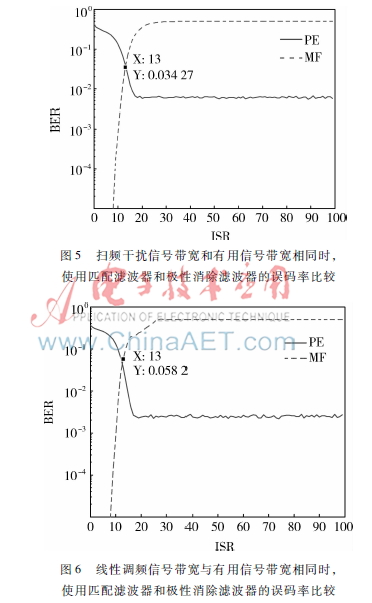
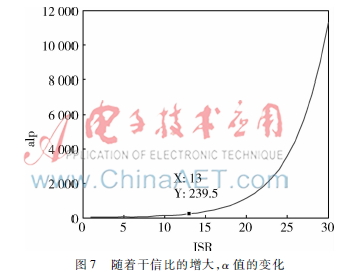
　　使用匹配濾波器和極性消除濾波器的誤碼率比較壓縮增益使得只有在干擾功率達(dá)到一定值后極性消除干擾抑制器才會(huì)工作,，在干信比較低時(shí)匹配濾波器足以抑制干擾,。由圖4可以看出，在變異系數(shù)策略中,，α的選擇十分重要,。而在圖5和6中可以看出，在干信比為13 dB時(shí),，需要對(duì)干擾抑制器的使用做出選擇,。圖7是在不同干信比條件下，CV2/CV1的變化曲線,，從圖中可知,，在干信比為13 dB時(shí)，CV2/CV1為239,，即設(shè)α=239對(duì)系統(tǒng)進(jìn)行仿真,，此時(shí)應(yīng)當(dāng)是一個(gè)最適宜的切換點(diǎn)，系統(tǒng)性能應(yīng)當(dāng)最佳　

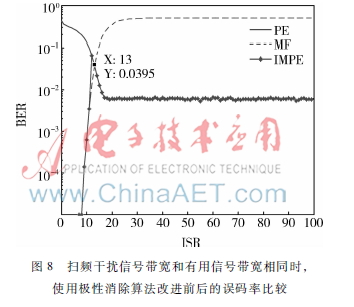
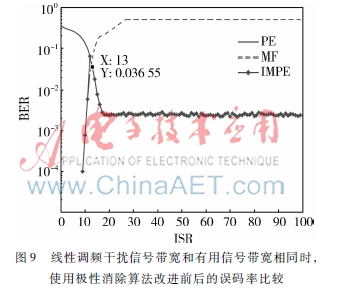
　　設(shè)α=239,，對(duì)接收信號(hào)的誤碼率進(jìn)行仿真,，如圖8和9所示?？梢钥闯?，該切換算法使得系統(tǒng)的性能在極性消除算法和匹配濾波器之間達(dá)到了最適宜的切換。比較圖8和9可以推斷,，只要干擾信號(hào)包絡(luò)幅度相同,，該切換策略對(duì)不同類(lèi)型的寬帶干擾信號(hào)均有效,。

4結(jié)論

　　針對(duì)直接擴(kuò)頻系統(tǒng)中的恒包絡(luò)干擾信號(hào)提出了一種極性消除算法。仿真結(jié)果表明,，該算法僅在干擾信號(hào)功率較高且為恒包絡(luò)時(shí)可以對(duì)信號(hào)進(jìn)行有效抑制,。本文提出了一種極性消除算法的改進(jìn)算法，通過(guò)引入變異系數(shù)的策略使得極性消除干擾抑制器只在干擾功率達(dá)到一定值后工作,，消除了寬帶恒包絡(luò)干擾信號(hào)對(duì)通信系統(tǒng)的影響,。仿真結(jié)果表明，只要干擾信號(hào)的包絡(luò)幅度相同,，當(dāng)干擾功率較高時(shí),，該改進(jìn)算法對(duì)不同類(lèi)型的寬帶恒包絡(luò)干擾信號(hào)均有效。該改進(jìn)算法不僅克服了極性消除算法在干擾功率較低時(shí)系統(tǒng)性能急劇下降的缺點(diǎn),，而且保留了其計(jì)算復(fù)雜度低的優(yōu)點(diǎn),。所有的仿真結(jié)果都證明了該改進(jìn)算法的有效性和變異系數(shù)作為切換策略的正確性。但該改進(jìn)算法依舊存在對(duì)干擾類(lèi)型有限制的缺點(diǎn),，可以考慮通過(guò)在該改進(jìn)算法的基礎(chǔ)上加入一盲自適應(yīng)均衡策略或者用盲自適應(yīng)濾波器代替快速傅里葉陷波模塊,。

參考文獻(xiàn)

　　［1］ PROAKIS J G. Digital communications ［M］. Beijing: Publishing House of Electronics Industry, 2013.

　?。?］ MILSTEIN L B. Interference rejection techniques in spread spectrum communications［C］. Proceedings of the IEEE, 1988, 76(6): 657671.

　?。?］ SAULNIER G J. Suppression of narrowband jammers in a spread spectrum receiver using transform domain adaptive filtering［C］. IEEE J.Select.Areas Commun., 1992, 10(4):742749.

　　［4］ HENTTU P. A new interference suppression algorithm against broadband constant envelope interference［C］. MILCOM 2000. 21st Century Military Communications Conference Proceedings, 2000: 742746.

　?。?］ Xia Caijie, Wang Aihua, An Jianping. Rejection of frequency sweeping interference in DSSS systems using improved polar exciser algorithm［C］. International Conference on Wireless Communications, Networking and Mobile Computing, 2007: 12281231.

　?。?］ VARTIAINEN J, LEHTOMAKI J, SAARNISAARI H, et al. Interference suppression in several transform domains［C］. Military Communications Conference, 2005. MILCOM 2005. 2005:22942300.