0 引言

    在無線通信中,，由于無線電波的多徑傳播而引起的碼間干擾嚴(yán)重影響通信質(zhì)量,，因此在接收端需要克服這些因素所帶來的影響,。盲均衡技術(shù)由于具有性能較好的信號(hào)恢復(fù)能力，因此被廣泛應(yīng)用在通信信號(hào)處理領(lǐng)域,。在盲均衡算法中,，常模盲均衡算法(Constant Modulus blind equalization Algorithm，CMA)主要適應(yīng)于低階調(diào)制信號(hào),，但對于高階調(diào)制信號(hào),，常模盲均衡算法的均衡效果比較差，容易產(chǎn)生較大的誤差,，而多模盲均衡算法(MMA)利用了均衡器輸出信號(hào)的幅度和相位信息,，有效克服了CMA單一判決圓造成的誤差^[1]。

    DNA遺傳算法是在傳統(tǒng)的遺傳算法基礎(chǔ)上發(fā)展而來的,，與傳統(tǒng)的遺傳算法不同,，DNA遺傳算法采用了組成DNA序列的四種堿基分子進(jìn)行編碼，從而提高了算法的編碼精度^[2-3],。由于DNA遺傳算法獨(dú)特的編碼特性,，因此便于模擬自然界生物遺傳進(jìn)化進(jìn)程，設(shè)計(jì)出更加貼近實(shí)際的操作算子,。DNA遺傳算法不僅繼承了傳統(tǒng)遺傳算法具有很強(qiáng)魯棒性的特點(diǎn),，而且還具有比傳統(tǒng)遺傳算法更有效的搜索性能^[4-5]。模擬退火算法(Simulated Annealing Algorithm,，SAA)是基于金屬退火的機(jī)理而建立起來的一種隨機(jī)算法,，它能夠通過控制溫度的變化過程來實(shí)現(xiàn)大范圍的粗略搜索和局部的精細(xì)搜索^[6-7]。由于DNA遺傳算法具有很強(qiáng)的全局搜索能力,，因此將DNA遺傳算法與模擬退火算法相結(jié)合,，能夠獲得全局搜索能力和局部搜索能力都較強(qiáng)的新算法。

    本文將基于模擬退火的DNA遺傳算法與小波多模盲均衡算法相結(jié)合,，提出了一種基于模擬退火的DNA遺傳優(yōu)化小波多模盲均衡算法(SADNAGA-WTMMA),，該算法通過對小波多模盲均衡算法的代價(jià)函數(shù)進(jìn)行優(yōu)化來獲得盲均衡算法均衡器權(quán)向量的最優(yōu)解。與多模盲均衡算法,、正交小波多模盲均衡算法(WTMMA)和基于DNA遺傳優(yōu)化的小波多模盲均衡算法(DNAGA-WTMMA)相比,，該算法在收斂速度和均方誤差方面都有顯著改善。

1 WTMMA算法

    圖1中,，a(k)=ar(k)+ja_i(k)是復(fù)信源發(fā)射信號(hào),，h(k)是信道脈沖響應(yīng)向量，y(k)=y_r(k)+jy_i(k)是均衡器輸入復(fù)信號(hào),，R_r(k)和R_i(k)分別是y_r(k)和y_i(k)經(jīng)過正交小波變換后的信號(hào),，n(k)是噪聲干擾信號(hào)。w(k)=[w_r0(k)+jw_i0(k),，…,，w_rL(k)+jw_iL(k)]^T(T表示轉(zhuǎn)置)是均衡器權(quán)向量,，z(k)=z_r(k)+jz_i(k)是均衡器的輸出信號(hào)。

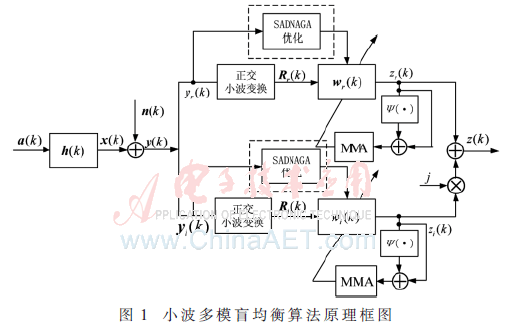
    均衡器輸出為：

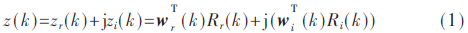
式中,，w_r(k),、w_i(k)分別表示均衡器權(quán)向量的實(shí)部與虛部。

    WTMMA的代價(jià)函數(shù)為：

式中,，分別表示對小波變換系數(shù)u_j,，m(k)和尺度變換系數(shù)s_J，m(k)的平均功率估計(jì),，可由下式遞推得到：

式中,，β為平滑因子，且0<β<1,。以上各式構(gòu)成了小波多模盲均衡算法(WTMMA)^[8],。

2 基于模擬退火算法的DNA遺傳算法

2.1 基于模擬退火算法的DNA遺傳算法操作算子

2.1.1 DNA編碼

    DNA編碼是將變量用A、T,、C,、G四種堿基表示的過程。首先建立堿基與數(shù)字的映射關(guān)系,，例如A/0,、T/1、C/2,、G/3映射,，然后變量表示成由0、1,、2,、3這四個(gè)數(shù)字表示的四進(jìn)制序列，這樣就建立了變量與堿基序列的映射關(guān)系,。

2.1.2 DNA遺傳算法交叉算子

    在交叉操作中包含三種類型的交叉算子,，分別為置換交叉算子、轉(zhuǎn)位交叉算子和重構(gòu)交叉算子,。

    （1）置換交叉算子

    置換交叉操作是最常見的一種交叉操作方式。該操作將兩個(gè)父體的等位基因片段相互交換,，從而得到新個(gè)體,。

    （2）轉(zhuǎn)位交叉算子

    轉(zhuǎn)位交叉操作是對一個(gè)個(gè)體進(jìn)行操作的。首先選擇一個(gè)個(gè)體作為父體,，然后在該父體序列中選取一段堿基片段并將其剪切下來插入自身序列中的某一位置,，生成新個(gè)體。

    （3）重構(gòu)交叉算子

    首先在種群中選取兩個(gè)父體A和B,，然后在父體A的末端剪切一段序列粘貼到父體B的首部,，并將父體B尾部多余的堿基序列切除,，同時(shí)隨機(jī)生成一段與被切除序列等長度的堿基片段粘貼到父體A的首部，即可獲得兩個(gè)新個(gè)體,。

2.1.3 自適應(yīng)變異概率

    為了提高DNA遺傳算法的收斂速度并實(shí)現(xiàn)對最優(yōu)解的全局搜索,，本文采用隨進(jìn)化代數(shù)變化的動(dòng)態(tài)變異概率。將種群中的個(gè)體DNA序列的前半段定義為高位部分,，后半段定義為低位部分,。高位部分和低位部分的變異概率分別如下所示：

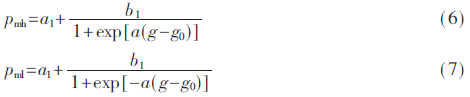
式中，p_mh和p_ml分別代表高位部分和低位部分的變異概率,，g表示當(dāng)前的進(jìn)化代數(shù),。

2.2 模擬退火算法

    模擬退火算法是一種基于物理中固體物質(zhì)退火機(jī)理的隨機(jī)搜索算法，通過控制溫度的變化過程進(jìn)行搜索,，局部搜索能力強(qiáng)^[9],。假設(shè)時(shí)刻t的溫度為T(t)，則模擬退火算法的降溫公式為：

式中,，T₀表示初始設(shè)定溫度,，k表示溫度下降系數(shù)。

    在SA的搜索過程中,，新解的產(chǎn)生是發(fā)生在當(dāng)前解的鄰域內(nèi),，采用如下公式進(jìn)行解變換：

式中，X_L和X_R分別為變量X左右邊界的值,，ε為(0,，1)之間的隨機(jī)數(shù)，U(0,，1)表示隨機(jī)選取0或1,，δ(T_i)為擾動(dòng)量，隨T_i的減小而減小,。T_i為T0時(shí),，δ(T_i)≤1，保證新的個(gè)體X′不會(huì)超出邊界,，且當(dāng)i→G時(shí),，δ(T_i)→0，滿足算法收斂的條件,。

    通過Meteopolis準(zhǔn)則來確定由X變?yōu)閄′的接受概率為：

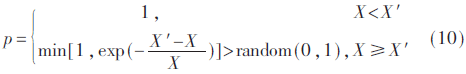
式中,，f_k+1為新解的適應(yīng)度，f_k為原解的適應(yīng)度,。根據(jù)Meteopolis準(zhǔn)則,，當(dāng)新解優(yōu)于原解時(shí)，接受新解作為當(dāng)前解；否則,，以概率p接受其為當(dāng)前解,。

3 SADNAGA-WTMMA操作步驟

3.1 確定適應(yīng)度函數(shù)

    為了獲得代價(jià)函數(shù)的最小值，定義適應(yīng)度函數(shù)為：

式中,，b>0,。

3.2 算法步驟

    步驟1：根據(jù)編碼規(guī)則設(shè)計(jì)初始種群Chrom=[w₁，w₂,，…,，w_M]，M為種群個(gè)體數(shù)量,，w_m(1≤m≤M)對應(yīng)一組均衡器權(quán)向量,。計(jì)算每個(gè)個(gè)體的適應(yīng)度值，根據(jù)個(gè)體適應(yīng)度值的大小將種群分位優(yōu)質(zhì)種群和劣質(zhì)種群,，同時(shí)保留優(yōu)質(zhì)種群中個(gè)體適應(yīng)度值最大的個(gè)體作為精英個(gè)體,。

    步驟2：在優(yōu)質(zhì)種群中執(zhí)行交叉操作。對被選中的個(gè)體分別執(zhí)行置換交叉和轉(zhuǎn)位交叉操作,。如果以上兩種交叉操作均為執(zhí)行,，則執(zhí)行重構(gòu)交叉操作。重復(fù)執(zhí)行以上交叉操作直到產(chǎn)生M/2新個(gè)體,，然后將這些新個(gè)體和父代種群個(gè)體一起組成混合種群,。

    步驟3：在混合種群中分別對每個(gè)個(gè)體執(zhí)行自適應(yīng)變異操作。變異操作完成后,，執(zhí)行聯(lián)賽選擇操作,，挑選出M-1個(gè)新個(gè)體，然后將這些新個(gè)體與精英個(gè)體一起組成種群規(guī)模為M的新種群,，進(jìn)化代數(shù)加1,，并且計(jì)算每個(gè)種群個(gè)體的適應(yīng)度值。

    步驟4：對種群個(gè)體進(jìn)行模擬退火操作,。設(shè)置退火算法計(jì)數(shù)器t以及最大退火代數(shù)t_max,，對種群中每個(gè)個(gè)體進(jìn)行模擬退火操作。分別按式(9)的新解變換規(guī)則將原解變換為新解,，然后根據(jù)式(10)計(jì)算出新解的接受概率,。根據(jù)Meteopolis準(zhǔn)則，式(10)的結(jié)果用來判斷是否接受新解為當(dāng)前解,，如果接受,，則t=t+1，否則,，t不變。如果t<t_max，則對個(gè)體繼續(xù)進(jìn)行模擬退火操作,，否則,，返回步驟(1)。

    步驟5：如果當(dāng)前進(jìn)化代數(shù)g<G_max,，則繼續(xù)對個(gè)體進(jìn)行模擬退火操作,，g=g+1；否則,，結(jié)束整個(gè)優(yōu)化過程,，輸出適應(yīng)度值最大的個(gè)體作為最優(yōu)個(gè)體。

4 仿真結(jié)果

    本文以MMA,、WTMMA和DNAGA-WTMMA為比較對象,，進(jìn)行仿真實(shí)驗(yàn)。仿真試驗(yàn)中,，信道h(k)=[0.313 2,，-0.104 0，0.890 8,，0.313 4],，信噪比為20 dB，均衡器權(quán)長為16,，采用64QAM信號(hào)作為發(fā)射信號(hào),，SADNAGA-WTMMA的種群規(guī)模為60，最大進(jìn)化為100代,，置換交叉操作,、轉(zhuǎn)位交叉操作和重構(gòu)交叉操作的執(zhí)行概率分別為p_c1=0.8，p_c2=0.5,，p_r=0.2,。模擬退火算法的初始溫度T₀=100，溫度下降系數(shù)k=0.95,，最大退火代數(shù)t_max=10,。各個(gè)算法的步長為：μ_MMA=0.6×10^-5，μ_WTMMA=1×10^-5,，μ_DNAGA-WTMMA=1.5×10^-6,，μ_{SADNAGA-WTMMA}=2×10^-6。

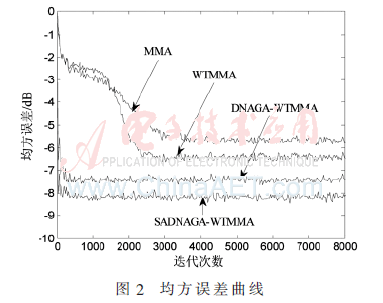
    實(shí)驗(yàn)采用500次蒙特卡洛仿真,。仿真結(jié)果如圖2所示,。圖2表明，與MMA,、WTMMA和DNAGA-QTMMA相比,，在穩(wěn)態(tài)誤差方面，SADNAGA-WTMMA比MMA低2.5 dB，比WTMMA低1.8 dB,，比DNAGA-WTMMA低0.8 dB,。在收斂速度方面，SADNAGA-WTMMA收斂速度最快,。圖3表明,，SADNAGA-WTMMA輸出的64QAM星座圖比另外三種算法輸出的星座圖更加清晰。

5 結(jié)論

    本文提出了一種基于模擬退火的DNA遺傳優(yōu)化小波多模盲均衡算法,。將模擬退火算法應(yīng)用到DNA遺傳算法中,，提高了DNA遺傳算法的搜索效率并且有效避免了局部收斂。仿真結(jié)果表明,，與MMA,、WTMMA和DNAGA-WTMMA相比，該算法在收斂速度和均方誤差方面都得到了提高,，因此更適合用于通信系統(tǒng)中的信號(hào)處理,。

參考文獻(xiàn)

[1] 郭業(yè)才.自適應(yīng)盲均衡技術(shù)[M].合肥：合肥工業(yè)大學(xué)出版社，2007：17-25.

[2] FAGHIHI V,，REINSCHMIDT K F,，KANG J H.Construction scheduling using genetic algorithm based on building information model[J].Expert Systems With Applications，2014,，41(16)：7565-7578.

[3] CHEN X,，WANG N.A DNA based genetic algorithm for parameter estimation in the hydrogenation reaction.Chemical Engineering Journal，2009,，150(2)：527-535.

[4] LI Y J,，LEI J.A feasible solution to the beam-angleoptimization problem in radiotherapy planning with a DNA-based genetic algorithm[J].IEEE Transactions on biomedical engineering，2010,，57(3)：499-508.

[5] 郭業(yè)才,，張冰龍，吳彬彬.基于DNA遺傳優(yōu)化的正交小波常模盲均衡算法[J].數(shù)據(jù)采集與處理,，2014,，29(3)：366-371.

[6] 賀小亮，畢義明.基于模擬退火遺傳算法的編隊(duì)對地攻擊火力分配建模與優(yōu)化[J].系統(tǒng)工程與電子技術(shù),，2014,，36(5)：900-904.

[7] JIANG J C，LIU H R,，F(xiàn)ENG H Z,，et al.Embedded static task allocation and scheduling base on simulated annealing and genetic algorithm[J].Journal of Computational Information Systems，2014,，10(4)：1465-1472.

[8] 郭業(yè)才,，胡苓苓,，丁銳.基于量子粒子群優(yōu)化的正交小波加權(quán)多模盲均衡算法[J].物理學(xué)報(bào)，2012,，61(5).

[9] 張昊,，陶然，李志勇,，等.基于自適應(yīng)模擬退火遺傳算法的特征選擇方法[J].兵工學(xué)報(bào)，2009,，30(1)：81-85.