劉斌，陳賢富,，程政

　?。ㄖ袊茖W(xué)技術(shù)大學(xué) 信息科學(xué)技術(shù)學(xué)院，安徽 合肥 230027）

　　摘要：車載導(dǎo)航系統(tǒng)中最重要的功能是路徑規(guī)劃,，傳統(tǒng)車載導(dǎo)航設(shè)備大多采用靜態(tài)算法,，沒有采用實(shí)時(shí)交通信息規(guī)劃出的路徑可能不是最優(yōu)路徑。結(jié)合一種動態(tài)行程時(shí)間表對傳統(tǒng)A*算法進(jìn)行調(diào)整,，可以有效利用路網(wǎng)實(shí)時(shí)交通數(shù)據(jù)規(guī)避擁堵路線,，從而實(shí)現(xiàn)動態(tài)路徑規(guī)劃。另外,，實(shí)際應(yīng)用中,，單一的優(yōu)化路徑往往不能滿足需求，對此提出重復(fù)路徑懲罰因子的概念,，構(gòu)造出了一種多路徑規(guī)劃算法,，可以在路徑相似度與路徑通行代價(jià)之間取得平衡，避免了傳統(tǒng)Ｋ最短路徑(K Shortest Paths, KSP)算法路徑相似度過高的缺點(diǎn),。

　　關(guān)鍵詞：動態(tài)路徑規(guī)劃,；A*算法；動態(tài)行程時(shí)間表；重復(fù)路徑懲罰因子,；KSP

0引言

　　路徑規(guī)劃算法是智能交通系統(tǒng)(Intelligent Transportation Systems, ITS)的重要組成部分之一,，盡管現(xiàn)實(shí)世界的實(shí)時(shí)交通信息在不斷變化，但目前大部分車載導(dǎo)航系統(tǒng)采用的仍是靜態(tài)的路徑規(guī)劃算法［1］,，如A*算法［2］,、Dijkstra算法［3］。此類算法假定道路通行代價(jià)不會改變,，大多采用道路長度,、寬度等靜態(tài)屬性作為路權(quán)計(jì)算方式，不能反映實(shí)時(shí)動態(tài)路況,。

　　針對動態(tài)路徑規(guī)劃算法,，參考文獻(xiàn)［4］采用D* star算法對A*算法進(jìn)行了改進(jìn)；參考文獻(xiàn)［5］針對道路的動態(tài)通行時(shí)間計(jì)算問題,，提出了一種路網(wǎng)中道路動態(tài)通行時(shí)間表,，表中記錄了每個(gè)路段每個(gè)時(shí)間段的行程時(shí)間，由此得出了車輛經(jīng)過路段的通行時(shí)間計(jì)算方法,。

　　以上算法在點(diǎn)對點(diǎn)的路徑規(guī)劃中,，只能得出單條優(yōu)化路徑，在實(shí)際應(yīng)用中往往不能滿足需求,。對此存在許多一次可以求出多條優(yōu)化路徑的算法,，稱為KSP算法。參考文獻(xiàn)［6］通過設(shè)置標(biāo)號的辦法得到K條最短路徑,；參考文獻(xiàn)［7］提出了一種新的多標(biāo)號算法來解決KSP問題,。但上述KSP算法均存在路徑相似度較高的缺點(diǎn)。參考文獻(xiàn)［8-9］提出的算法可以求出一組邊不相交鏈路,，但各條路徑相差較大,。

　　本文通過分析上述算法的優(yōu)缺點(diǎn)，結(jié)合A*算法與動態(tài)行程時(shí)間表,，為減少接收行程時(shí)間表時(shí)的通信量,，結(jié)合矩形限制搜索區(qū)域算法［10］，給出了一種求解單一優(yōu)化路徑的動態(tài)路徑規(guī)劃算法,。同時(shí)提出一種重復(fù)路徑懲罰因子,，可以利用它一次搜索出多條優(yōu)化路徑，所求得的K條路徑可以兼顧路徑相似度與路徑通行代價(jià),。

1A*算法

　　A*算法是一種典型的啟發(fā)式搜索算法,，建立在Dijkstra算法的基礎(chǔ)之上，廣泛應(yīng)用于游戲地圖,、現(xiàn)實(shí)世界中,，用來尋找兩點(diǎn)之間的最短路徑。A*算法最主要的是維護(hù)了一個(gè)啟發(fā)式估價(jià)函數(shù)，如式(1)所示,。

　　f(n)=g(n)+h(n)(1)

　　其中,，f(n)是算法在搜索到每個(gè)節(jié)點(diǎn)時(shí)，其對應(yīng)的啟發(fā)函數(shù),。它由兩部分組成,，第一部分g(n)是起始節(jié)點(diǎn)到當(dāng)前節(jié)點(diǎn)實(shí)際的通行代價(jià)，第二部分h(n)是當(dāng)前節(jié)點(diǎn)到終點(diǎn)的通行代價(jià)的估計(jì)值,。算法每次在擴(kuò)展時(shí),，都選取f(n)值最小的那個(gè)節(jié)點(diǎn)作為最優(yōu)路徑上的下一個(gè)節(jié)點(diǎn)。

　　在實(shí)際應(yīng)用中,，若以最短路程為優(yōu)化目標(biāo)，h(n)常取作當(dāng)前點(diǎn)到終點(diǎn)的歐幾里得距離(Euclidean Distance)或曼哈頓距離(Manhattan Distance)等,。若令h(n)=0,，表示沒有利用任何當(dāng)前節(jié)點(diǎn)與終點(diǎn)的信息，A*算法就退化為非啟發(fā)的Dijkstra算法,，算法搜索空間隨之變大,，搜索時(shí)間變長。

　　A*算法步驟如下,，算法維護(hù)兩個(gè)集合：P表與Q表,。P表存放那些已經(jīng)搜索到、但還沒加入最優(yōu)路徑樹上的節(jié)點(diǎn),；Q表維護(hù)那些已加入最優(yōu)路徑樹上的節(jié)點(diǎn),。

　　（1）P表,、Q表置空,，將起點(diǎn)S加入P表，其g值置0,，父節(jié)點(diǎn)為空,，路網(wǎng)中其他節(jié)點(diǎn)g值置為無窮大。

　?。?）若P表為空,，則算法失敗。否則選取P表中f值最小的那個(gè)節(jié)點(diǎn),，記為BT,，將其加入Q表中。判斷BT是否為終點(diǎn)T,，若是,，轉(zhuǎn)到步驟（3）；否則根據(jù)路網(wǎng)拓?fù)鋵傩院徒煌ㄒ?guī)則找到BT的每個(gè)鄰接節(jié)點(diǎn)NT，進(jìn)行下列步驟:

　?、儆?jì)算NT的啟發(fā)值

　　f(NT)=g(NT)+h(NT)(2)

　　g(NT)=g(BT)+cost(BT, NT)(3)

　　其中,cost(BT, NT)是BT到NT的通行代價(jià),。

　　②如果NT在P表中,，且通過式(3)計(jì)算的g值比NT原先的g值小,，則將NT的g值更新為式(3)結(jié)果，并將NT的父節(jié)點(diǎn)設(shè)為BT,。

　?、廴绻鸑T在Q表中，且通過式(3)計(jì)算的g值比NT原先的g值小,，則將NT的g值更新為式(3)結(jié)果,，將NT的父節(jié)點(diǎn)設(shè)為BT，并將NT移出到P表中,。

　?、苋鬘T既不在P表，也不在Q表中,，則將NT的父節(jié)點(diǎn)設(shè)為BT,，并將NT移到P表中。

　?、蒉D(zhuǎn)到步驟（2）繼續(xù)執(zhí)行,。

　　（3）從終點(diǎn)T回溯,，依次找到父節(jié)點(diǎn),，并加入優(yōu)化路徑中，直到起點(diǎn)S,，即可得出優(yōu)化路徑,。

2動態(tài)行程時(shí)間表及A*算法調(diào)整

　　2.1動態(tài)行程時(shí)間表

　　為計(jì)算在實(shí)時(shí)情況下某段道路的通行時(shí)間，采用了一種道路通行時(shí)間表的結(jié)構(gòu),，表中存放了道路當(dāng)前時(shí)刻的通行時(shí)間以及未來幾個(gè)時(shí)刻通行時(shí)間的預(yù)測值,。

　　以t0表示導(dǎo)航系統(tǒng)開始工作的時(shí)刻，將未來一段時(shí)間劃分為若干個(gè)時(shí)段,，以ΔT表示一個(gè)時(shí)段的長度,，系統(tǒng)開始工作的時(shí)刻屬于第一個(gè)時(shí)段。然后對這些時(shí)段進(jìn)行編號,，如1,2,3,4,，…。同理,，也將每條道路編號為1,2,3,4,，…,。采用Tij表示路段i在時(shí)段j的通行時(shí)間。這樣就可得到不同道路在不同時(shí)刻的通行時(shí)間,，將它們記錄為表1,。 

　　車載系統(tǒng)可能會在某個(gè)時(shí)刻進(jìn)行路徑規(guī)劃，優(yōu)化路徑上可能會包含多個(gè)路段,，將它們編號為1,2,3,…,，k,…。以［tk,tk′］表示車輛經(jīng)過路段k的通行時(shí)間Tk,則Tk= tk′-tk,。車輛可能會花費(fèi)多個(gè)時(shí)段才能通過路段k,，將這些時(shí)段與通行時(shí)間Tk1′,Tk2′,Tk3′,…對應(yīng)。

　　首先計(jì)算出車輛經(jīng)過路段k起點(diǎn)的時(shí)刻對應(yīng)的時(shí)段fk:

　　其中,，」符號表示對結(jié)果取下整,。則相應(yīng)地可得出：

　　T′ki=Tk(fk+i-1)(5)

　　根據(jù)時(shí)段長度ΔT、道路長度L與道路通行速度的不同取值,，可能會出現(xiàn)車輛只需在一個(gè)時(shí)段即可通過路段,，也可能需要多個(gè)時(shí)段才能通過。因此經(jīng)過牛頓運(yùn)動學(xué)原理進(jìn)行計(jì)算,，可得到車輛通過路段k的具體公式如下［9］：

　　其中，m的取值滿足：

　　2.2A*算法調(diào)整

　　在得出車輛通過路段k的計(jì)算方法后,，即可對傳統(tǒng)A*算法進(jìn)行調(diào)整,，以搜索出動態(tài)優(yōu)化路徑。具體如下：

　　在A*算法描述的第（2）步中,，首先計(jì)算出起點(diǎn)S到達(dá)BT的通行時(shí)間t,，則到達(dá)BT的時(shí)刻為出發(fā)時(shí)刻加上t，記為tBT,，然后根據(jù)式(6)計(jì)算出BT到達(dá)NT的通行時(shí)間T,。則可更新g(NT)為：

　　g(NT)=g(BT)+T+tli(8)

　　其中，tli表示路口紅綠燈等待時(shí)間,。除了這些調(diào)整外,，前述A*算法的其他部分不需要改變。

3動態(tài)多路徑規(guī)劃算法

　　3.1算法描述

　　上述調(diào)整后的A*算法一次只能搜索出單條動態(tài)優(yōu)化路徑,，為了在給定起點(diǎn)S與終點(diǎn)T之后得到多條在通行代價(jià)與路徑相似度之間取得平衡的動態(tài)優(yōu)化路徑,，提出了一種重復(fù)路徑懲罰因子的概念。算法的總體思想是：首先利用上述調(diào)整后的A*算法搜索出一條優(yōu)化路徑后,，將此優(yōu)化路徑上每條道路的通行代價(jià)都乘以懲罰因子,，然后再利用算法搜尋下一條優(yōu)化路徑。在描述算法之前,，首先需要定義幾個(gè)符號：Pk為S到T之間的第k條優(yōu)化路徑,；Lk為Pk的長度,；PC為存放優(yōu)化路徑的集合；OLnk為第n條優(yōu)化路徑與第k條優(yōu)化路徑的重合度,，表示為兩條路徑上重復(fù)路段的總長度, k=n-1,n-2,…,，1；Dnk為第n條優(yōu)化路徑與第k條優(yōu)化路徑的相似度,，Dnk=OLnk/Ln,k=n-1,n-2,…,，1；MO為設(shè)定的最大相似度,；PO為重復(fù)路徑懲罰因子,，PO=(1MO)β,β為一個(gè)正系數(shù)；K為希望搜索出的最大優(yōu)化路徑條數(shù),；n為當(dāng)前已規(guī)劃出優(yōu)化路徑條數(shù),。

　　利用這些符號，算法可描述如下：

　?。?）設(shè)置MO,、β和K，令n=0;

　?。?）利用調(diào)整后的A*算法搜索出一條優(yōu)化路徑,將其加入PC中,，n=1;

　　（3）若n大于等于K,，算法結(jié)束,，否則將Pn上每一條路段的通行代價(jià)都乘以PO;

　　（4）路徑規(guī)劃與相似度計(jì)算：

　?、賜=n+1;

　?、?利用改造A*算法規(guī)劃出下一條優(yōu)化路徑Pn;

　　③ 計(jì)算相似度：

　　Dnk=OLnk/Ln,，k=n-1,n-2,…,，1

　　④路徑相似度判斷：

　　若Dnk>MO,，算法結(jié)束,，否則將Pn加入 PC，轉(zhuǎn)步驟（3）,。

　　利用此算法最多可以求出K條優(yōu)化路徑,，各條優(yōu)化路徑的通行代價(jià)與相似度取決于MO與β的取值。當(dāng)MO=1.0時(shí),，相當(dāng)于沒有懲罰,，此時(shí)只能得出一條路徑；當(dāng)MO<1.0時(shí),可以得到多條路徑,。

　　3.2實(shí)驗(yàn)結(jié)果

　　圖1本文算法規(guī)劃結(jié)果本文采用真實(shí)的合肥城區(qū)電子地圖數(shù)據(jù),，構(gòu)建了一個(gè)C/S(Client/Server)模型,，由服務(wù)器端模擬產(chǎn)生實(shí)時(shí)交通數(shù)據(jù)，每條道路的通行時(shí)間范圍為道路暢通時(shí)的時(shí)間到7倍于它之間的一個(gè)隨機(jī)值,。在車載終端請求實(shí)時(shí)數(shù)據(jù)時(shí),，終端會發(fā)送起點(diǎn)、終點(diǎn)坐標(biāo)值給服務(wù)器,，服務(wù)器采用矩形限制搜索區(qū)域算法,大大減少了通信的數(shù)據(jù)量,。

　　以從“中國科學(xué)技術(shù)大學(xué)第一教學(xué)樓”到“安徽大學(xué)新校區(qū)”為例，規(guī)劃結(jié)果如圖1所示,。 其中的參數(shù)設(shè)置為：MO=0.5,，β=1.8，K =3,。優(yōu)化3條路徑,。路徑長度與相似度統(tǒng)計(jì)如表2所示。

　　表2優(yōu)化路徑通行代價(jià)與相似度路徑123長度/km13.4315.9216.37最大相似度/%-13.6330.78其中最大相似度表示的是此道路與標(biāo)號小于它的那些道路的最大D值,。作為對比,，百度地圖的搜索結(jié)果如圖2所示?！?/p>

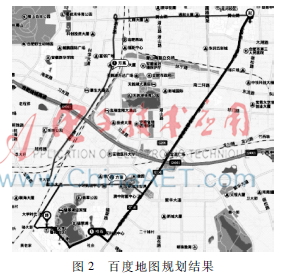
　　3條道路的長度分別為14.3 km,、16.4 km與19.1 km。

4結(jié)論

　　在本文中,，提出了一種基于傳統(tǒng)A*搜索算法,，并結(jié)合動態(tài)通行時(shí)間表、矩形限制搜索區(qū)域算法與道路相似度懲罰因子的多優(yōu)化路徑規(guī)劃算法,。實(shí)驗(yàn)結(jié)果顯示，在給定起點(diǎn)和終點(diǎn)的情況下,，本文提出的算法能有效規(guī)劃出在通行代價(jià)與路徑相似度之間取得平衡的多條路徑,，有效解決了傳統(tǒng)KSP算法路徑相似度過高的缺點(diǎn)，同時(shí)提高了算法的實(shí)時(shí)性,。

　　參考文獻(xiàn)

　?。?］ NADI S, DELAVAR M R. Locationbased service for Invehicle route guidance with real time traffic information［C］.The 12th World Conference on Transport Research (WSTR to WCTR) Proceedings, 2010: 110.

　　［2］ GOLDBERG A V, KAPLAN H, WERNECK R F. Reach for A*: efficient pointtopoint shortest path algorithms［C］.ALENEX, 2006, 6(2): 129143.

　?。?］ MHRING R H, SCHILLING H, SCHTZ B, et al. Partitioning graphs to speed up Dijkstra’s algorithm［M］.Experimental and Efficient Algorithms. Springer Berlin Heidelberg, 2005,11(28): 189202.

　?。?］ 隨裕猛, 陳賢富, 劉斌. Dstar Lite 算法及其動態(tài)路徑規(guī)劃實(shí)驗(yàn)研究［J］. 微型機(jī)與應(yīng)用, 2015, 34(7): 1619.

　　［5］ 蘇永云, 晏克非. 車輛導(dǎo)航系統(tǒng)的動態(tài)最優(yōu)路徑搜索方法研究［J］. 系統(tǒng)工程, 2000, 18(4): 3237.

　?。?］ DREYFUS S E. An appraisal of some shortestpath algorithms［J］. Operations research, 1969, 17(3): 395412.