孫汝峰,，劉順蘭

　?。ê贾蓦娮涌萍即髮W 通信工程學院，浙江 杭州 310018）

　　摘要：提出了一種基于高階累積量和譜分析識別多種數(shù)字調(diào)制信號的算法,。首先根據(jù)各調(diào)制信號四階和八階累積量的不同,，定義一個特征參數(shù)實現(xiàn)信號的類間識別；其次根據(jù)不同調(diào)制信號二次方譜與四次方譜的不同,，提取出相應的特征參數(shù),，從而實現(xiàn)信號的類內(nèi)識別。仿真實驗結果表明,，該方法在較低信噪比條件下可以對2/4/8PSK,、2/4/8FSK信號實現(xiàn)識別，且識別率較高,，具有很強的實用性,。

　　關鍵詞：調(diào)制識別；高階累積量,；二次方譜,；四次方譜

0引言

　　通信信號的調(diào)制識別在電子偵察和無線電監(jiān)控等領域占據(jù)著十分重要的地位，主要任務是在調(diào)制信息未知的情況下確定調(diào)制信號的調(diào)制方式以及估計信號的一些參數(shù)（如載波頻率,、波特率等）,，為之后的信號分析處理提供依據(jù)。

　　近年來國內(nèi)外提出了很多比較有效的調(diào)制信號識別方法，主要可以分為決策理論方法和特征參數(shù)模式識別方法［1-4］,，其中決策論方法需要的先驗知識較多［1］,，相比較下特征參數(shù)模式識別的方法更為實用，常用的特征參數(shù)模式分類特征有信號的瞬時特征,、高階累積量特征,、小波變換特征、譜相關特征等,。參考文獻［2］基于信號瞬時特征識別對噪聲比較敏感,，在低信噪比的環(huán)境下識別率比較低。參考文獻［3］利用四階累積量實現(xiàn)2PSK,、4PSK和8PSK信號的分類,，并證明高階累積量對信號星座圖的平移，尺度和相位旋轉等變換具有不變性,。這種方法對于識別少數(shù)的信號具有不錯的性能,，但是對于識別較多的調(diào)制信號僅僅基于高階累積量特征的識別需要信號序列的統(tǒng)計信息，需要較大的樣本空間才能得到良好的識別效果,，無疑增加了算法復雜度,，并且MFSK信號的高階累積量值都相同，直接運用高階累積量無法識別出MFSK信號,。參考文獻［4］基于小波變換,，則需要信號精確的相位信息。參考文獻［5］通過分析信號的譜相關平面圖,，提取出一組譜相關特征參數(shù)來實現(xiàn)對信號的識別,。

　　本文提出一種基于高階累積量與譜分析的調(diào)制識別方法。利用高階累積量提取更少的特征參數(shù)對信號進行類間識別,。利用不同信號經(jīng)過非線性變換后譜線特征的不同提取信號的特征參數(shù)對信號進行類內(nèi)識別,在低信噪比環(huán)境下實現(xiàn)更高的識別率,。計算機仿真結果驗證了算法的實用性和有效性。

1信號模型

　　一般情況下接收到的受噪聲污染過的數(shù)字調(diào)制信號的模型可表示為［5］：

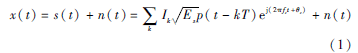
　　其中,，k=1,2,3,...,N,N為發(fā)送碼元序列的長度,，Ik表示碼元序列，p(t)為基帶碼元波形,，T為碼元寬度,，fc為載波頻率，θc為載波相位,，Es為發(fā)送碼元波形的能量,n(t)為零均值的高斯白噪聲,。

　　接收端對接收信號進行預處理，假設載波頻率,、相位,、定時同步,，下變頻后的復基帶信號可以表示為［6］:

　　其中，Δθc為載波相位差,。

　　調(diào)制信號的類型不同,，Ik的表達形式也不一樣，具體如下：

　　對MPSK信號：

　　Ik=ak+jbk∈{ej2π(m－1)/M,m=1,2,...,M}(3)

　　對MFSK信號：

　　Ik=ej2πfkt(4)

　　其中,，fk∈{(2m－1－M)Δf,m=1,2,...,M} ,，Δf為信號的頻率間隔。

2高階累積量和高階矩

　　對于一個具有零均值的復隨機過程X(t),，其高階矩定義為［7］：

　　Mpq=E［X(t)(p－q)X*(t)q］(5)

　　其中,，E［·］表示求期望運算。

　　累積量定義為［8］：

　　Cpq=Cum{X(t),…,X(t),X*(t),…,X*(t)}(6)

　　其中,，X(t)為p－q項,，X*(t)為q項。Cum為累積矩,，* 表示函數(shù)的共軛,。

　　常用的累積量與矩的關系如下［9］：

　　C20=M20(7)

　　C21=M21(8)

　　C40=M40－3M220(9)

　　C42=M42－|M20|2－2M221(10)

　　C60=M60－15M40M20+30M320(11)

　　C63=M63－6M41M20－9M42M21+18M220M21+12M321(12)

　　C80=M80－28M20M60－35M240+420M220M40－630M420(13)

　　因發(fā)送信號s(t)與高斯白噪聲n(t)兩者獨立，根據(jù)累積量的性質(zhì)由式（1）可得：

　　Cum(x(t))=Cum(s(t))+Cum(n(t))(14)

　　由于零均值高斯白噪聲大于二階的累積量值為零,，則式(14)也可表示為：Cum(x(t))=Cum(s(t)),。即接收信號的高階累積量值等于發(fā)送信號的高階累積量值,，據(jù)此可以消除高斯白噪聲的影響,。

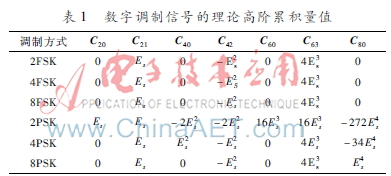
　　假設符號發(fā)送概率相等，信號能量為Es,，且無高斯噪聲影響,，采用總體平均代替統(tǒng)計平均的方法［10］，可以得到各種調(diào)制信號的高階累積量理論值,，具體如表1所示,。

3基于信號高階累積量實現(xiàn)調(diào)制信號的類間識別

　　分析表1可以看出，MFSK與MPSK的C80值存在著較大的差別,，可以利用C80這個值實現(xiàn)MFSK與MPSK的類間識別,。本文定義特征參數(shù)F如下：

　　特征參數(shù)選取信號的八階和四階累積量，可以減小噪聲的影響,，采用絕對值形式可以減小相位抖動對特征參數(shù)的影響,，采用比值的形式可以消除幅度對特征參數(shù)的影響。根據(jù)表1可以得到各調(diào)制信號的F值,，具體如表2所示,。

　　4調(diào)制信號的譜線特征

　　由于不同的調(diào)制信號經(jīng)過非線性變換后，其頻譜會呈現(xiàn)不一樣的譜線特征,，因此利用譜線特征可以實現(xiàn)信號的類內(nèi)識別,。

　　4.1MPSK的二次方譜與四次方譜的譜線特征

　　對于4PSK信號，表達形式如式(2)所示，Ik如式(3)所示,。不失一般性,，其中ak+jbk∈22{1+j,1－j,－1+j,－1－j}，p(t)為升余弦型脈沖,，滾降系數(shù)α取0<α<0.5,，并假設Δθc=0。則信號二次方形式的統(tǒng)計期望值為：

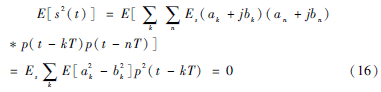
　　參考文獻［11］分析了信號的譜線生成特性,，當E［s2(t)］具有周期時變性時,，其頻域（二次方譜）會產(chǎn)生出離散的譜線。而對4PSK信號,，由式(16)可知E［s2(t)］=0,，因此不具有周期時變性，所以其二次方譜不存在離散譜線,。

　　同理,，4PSK四次方形式的統(tǒng)計期望值為：

　　式(17)是一個以T為周期的函數(shù)，其頻域會產(chǎn)生離散譜線,，相應的傅里葉變換形式（信號的四次方譜）為：

　　同理可以分析得到,，2PSK信號的二次方譜和四次方譜均存在譜線，8PSK信號的二次與四次方譜均不存在譜線,。圖1給出了無噪聲干擾下4PSK的譜線特征圖,。

　　4.2MFSK的二次方譜的譜線特征

　　根據(jù)之前分析，MFSK的等效復低通信號形式可用式(2)表示,，其中Ik用式(4)表示,。不失一般性，p(t)為升余弦型脈沖［12］,，滾降系數(shù)α取0<α<0.5,。以2FSK信號為例，2FSK信號做二次方譜為：

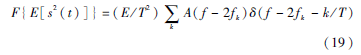
　　其中,，A(f)=F{p2(t)},，由于α<0.5的限制，由式(19)可知2FSK信號的二次方譜在±2Δf處有兩條明顯譜線,。同理分析可得,，4FSK信號的二次方譜在±2Δf、±6Δf處有4條譜線,，8FSK信號的二次方譜在±2Δf,±6Δf,±10Δf,±14Δf處有8條譜線,。

　　5基于信號的譜線特征實現(xiàn)調(diào)制信號的類內(nèi)識別

　　對于MPSK信號，由于其不同階數(shù)的PSK信號特征參數(shù)F的值不同,，可以通過本文定義的F值實現(xiàn)類內(nèi)識別,。但是本文建議采用MPSK信號的二次方譜和四次方譜零頻處是否存在譜線作為識別特征值,。如果信號的二次方譜在零頻位置處存在譜線，令其特征參數(shù)f1=1,，否則f1=0,。如果信號的四次方譜在零頻位置處存在譜線，令其特征參數(shù)f2=1,，否則f2=0,。定義N_p=［f1,f2］，據(jù)之前的分析,，MPSK信號的N_p值表示如下：

　　由式(20)可以實現(xiàn)MPSK信號的類內(nèi)識別,。

　　對于MFSK信號，由于其二次方譜的譜線個數(shù)對應信號的M值,，因此這里提取特征參數(shù)N_f,，如果其所測信號二次方譜中譜線的個數(shù)N_f=2，則為2FSK信號,；如果N_f=4,，則為4FSK信號；如果N_f=8,，則為8FSK信號,。

　　本文建議的基于高階累積量和譜分析的數(shù)字調(diào)制信號識別流程圖如圖2所示。

6性能仿真與分析

　　設MPSK,、MFSK信號的載波頻率為5 kHz,采樣頻率為40 kHz,，碼元速率為1 000 b/s，且MFSK的頻率間隔為5 kHz,，數(shù)據(jù)長度N=2 000,，加性噪聲為高斯白噪聲,。在相同的信噪比環(huán)境下,，對信號進行100次獨立試驗［1314］。

　　由于特征參數(shù)F的幅度范圍比較大,，為觀察方便,，將其劃分為兩段（［05］,［2080］）。分別繪制出調(diào)制信號的特征參數(shù)F隨信噪比變化曲線,，如圖3所示,。

　　從圖3可以看出，MFSK與MPSK信號的F值都比較接近于前面計算的理論值,，兩者的F值存在著較為明顯的差別,，這就說明了可以利用F值來實現(xiàn)兩者的類間識別。選取F=1作為類間識別的閾值,，當信號的F值大于1的時候,，信號判定為MPSK信號,，否則判定為MFSK信號。

　　在實現(xiàn)MFSK與MPSK信號的類間識別仿真之后,，利用上述所提的特征參數(shù)根據(jù)算法流程對兩者進行類內(nèi)識別的仿真,。同一信噪比，對所有信號進行500次獨立試驗,，取識別正確的次數(shù)和識別總次數(shù)的比值為信號的識別率,，取信號的類間識別率與類內(nèi)識別率的乘積作為信號的總識別率，仿真結果如圖4所示,。

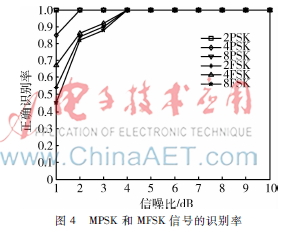
　　由圖4可知,，采用本文建議的方法，MPSK信號在信噪比為1 dB情況下,，2PSK,、4PSK、8PSK信號的識別率分別為100%,、85%,、100%；當信噪比大于2 dB時,，3種PSK信號的識別率都達到了100%,。MFSK信號在信噪比為1 dB的情況下，2FSK,、4FSK,、8FSK信號的識別率分別為54%、67%,、45%,；當信噪比等于3 dB時，3種FSK信號信號的識別率達到了85%以上,；當信噪比大于等于4 dB時,，3種FSK信號信號的識別率達到了100%。由此可見,，本文建議的方法在低信噪比下也取得了較高的識別率,。MFSK信號的識別率在信噪比較低的情況下比MPSK信號的識別率要低，分析原因主要是因為受噪聲影響類間識別的特征值F在信噪比低的情況下要比理論值偏大,，在對MFSK信號識別時,，會出現(xiàn)大于閾值的情況，導致判斷出錯,。

　　參考文獻［9］中分別采用高階累積量的特征值和微分后的累積量構造特征值的方法來識別MPSK和MFSK信號,，在相同的仿真實驗環(huán)境和信號參數(shù)設置，本文方法與參考文獻［9］進行性能對比試驗,，其對比結果如表3所示,。從表3可以看出,，相比參考文獻［9］，在相同條件下本文所提方法的識別性能顯著提高,。 

7結論

　　本文基于高階累積量和譜分析的理論知識,，定義了一個基于信號八階累積量和四階累積量的特征參數(shù)F，用來實現(xiàn)MFSK和MPSK信號的類間識別,。由于高斯白噪聲高于二階的累積量值為零,，因此此方法具有很好的抗噪聲性能。根據(jù)不同信號的二次方譜與四次方譜的譜線特性不同,，分別提取出特征參數(shù)N_p和N_f對MPSK和MFSK信號實現(xiàn)類內(nèi)識別,。計算機仿真結果表明，此方法在低信噪比的情況下可以取得理想的識別率,，證明了此方法的有效性,，抗噪聲性能較強。

參考文獻

　?。?］ NANDI A K,AZZOUZ E E.Algorithms for automatic modulation recognition of communication signals［J］.IEEE Transactions on Communication, 1998, 46(4):431436.

　?。?］ 位小記，謝紅,，郭慧.基于瞬時特征參數(shù)的數(shù)字調(diào)制識別算法［J］. 傳感器與微系統(tǒng),，2011,30（1）：127130.

　　［3］ 陳衛(wèi)東,，楊紹全.利用累量不變量對MPSK信號分類［J］.西安電子科技大學學報,，2002，29（2）：229232.

　?。?］ 胡建偉,，湯建龍，楊紹全.使用小波變換的MPSK信號調(diào)制類型識別［J］.電路與系統(tǒng)學報,，2006,11（3）,，130134.

　　［5］ 韓國棟,，蔡斌,，鄔江興.調(diào)制分析與識別的譜相關方法［J］.系統(tǒng)工程與電子技術,，2001,23（3）：3436.

　?。?］ 徐曉瑤，劉娟,楊東.多徑信道下MPSK 信號調(diào)制識別算法的研究［J］.電子技術應用,，2010,36(2):103106.

　?。?］ PROAKIS J G． Digital communicatio （4th edition）［M］． NewYork: McGrawHillBook Co．，2001．

　?。?］ 劉獻玲.基于累量的OFDM信號調(diào)制識別［D］.西安：西安科技大學,，2007.