李慶1,，謝一首1,，鄭力新1，周凱汀2,張?jiān)＠?

　?。?.華僑大學(xué) 工學(xué)院,，福建 泉州 362021；2.華僑大學(xué) 信息科學(xué)與工程學(xué)院,，福建 廈門 361021）

　　摘要：根據(jù)STEPSA1400型工業(yè)機(jī)器人的具體結(jié)構(gòu)特點(diǎn)，建立了機(jī)器人的運(yùn)動(dòng)學(xué)方程,，使用只需一次矩陣逆乘的逆解方法,，求出逆解。與常規(guī)求解方法相比,，此方法減少了多次矩陣逆乘帶來的計(jì)算量,。在解的表達(dá)式中，采用雙變量正切函數(shù)以避免解的丟失,。針對多重解問題,，采用“最短行程”原則，選取與當(dāng)前關(guān)節(jié)角度值的歐氏距離較小的解作為逆解結(jié)果,。最后,，使用MATLAB編寫程序，對文中推導(dǎo)出的方程進(jìn)行驗(yàn)證與仿真,，實(shí)驗(yàn)結(jié)果證明了解的準(zhǔn)確性和可行性,。對該型機(jī)器人的運(yùn)動(dòng)學(xué)分析與仿真為其后的離線編程、軌跡規(guī)劃等打下了基礎(chǔ),，同時(shí),，文中的方法與思想也適用于其他關(guān)節(jié)型機(jī)器人。

　　關(guān)鍵詞：工業(yè)機(jī)器人,；SA1400機(jī)器人,；六自由度,；逆運(yùn)動(dòng)學(xué)；最短行程,；MATLAB仿真

0引言

　　華僑大學(xué)研究生科研創(chuàng)新能力培育計(jì)劃資助項(xiàng)目（1400422004）近年來,，隨著經(jīng)濟(jì)和社會的發(fā)展，我國出現(xiàn)人力成本上漲,、勞動(dòng)力供給減少以及制造業(yè)就業(yè)意愿下降的現(xiàn)象,，這些現(xiàn)象嚴(yán)重制約了我國制造業(yè)的國際競爭力。于是一些企業(yè)開始把目光投向“機(jī)器換人”,，利用自動(dòng)化技術(shù)來建設(shè)無人化工廠以解決當(dāng)前困局,，制造業(yè)的轉(zhuǎn)型升級已是大勢所趨。面對德國提出的“工業(yè)4.0”,，我國出臺的“中國制造2025”將重點(diǎn)發(fā)展工業(yè)機(jī)器人與新一代信息技術(shù)等領(lǐng)域,，“智能制造”成為了中國制造的主攻方向，而機(jī)器人也成為這一主題下最受關(guān)注的領(lǐng)域之一,。實(shí)現(xiàn)“中國制造2025”,，最重要的智能部件就是網(wǎng)絡(luò)化的機(jī)器人，機(jī)器人產(chǎn)業(yè)將成為未來幾十年內(nèi)全球制造業(yè)的角力場,。2013年,，中國工業(yè)機(jī)器人的總銷量為3.7萬臺，成為世界第一的機(jī)器人大國,，也是全球增長速度最快的機(jī)器人市場,。2014年，全球工業(yè)機(jī)器人的銷量為22.9萬臺,，中國內(nèi)地售出5.7萬臺,，占全球銷量的四分之一［1］。

　　目前,，機(jī)器人正解的求法已比較統(tǒng)一,，而逆解的求解方法有多種，主要分為封閉解法和數(shù)值解法,。封閉解法又分為代數(shù)解法和幾何解法,。封閉解法計(jì)算速度快、效率高,、便于實(shí)時(shí)控制,，而數(shù)值解法因其迭代性質(zhì)，使其求解速度較慢,，所以大多數(shù)情況下都是使用封閉解法［23］,。逆解過程中，一般在關(guān)節(jié)角度范圍內(nèi)計(jì)算機(jī)器人關(guān)節(jié)角度，文獻(xiàn)［4］在解關(guān)節(jié)角時(shí)采用單變量反正切函數(shù),，可能造成一個(gè)解的丟失,。機(jī)器人逆解存在多解，如文獻(xiàn)［5］中就有8組解,，但控制機(jī)器人只能有一組解,，而文中沒有給出選取最優(yōu)解的方法。

1運(yùn)動(dòng)學(xué)模型的建立

　　本文根據(jù)上海新時(shí)達(dá)機(jī)器人有限公司SA系列工業(yè)機(jī)器人中的1400型機(jī)器人的特點(diǎn)進(jìn)行研究,。SA1400型機(jī)器人有6個(gè)自由度,，而且6個(gè)關(guān)節(jié)均為旋轉(zhuǎn)關(guān)節(jié)。為了描述機(jī)器人各連桿之間的相對位置和方向關(guān)系,，需要根據(jù)關(guān)節(jié)結(jié)構(gòu)在每個(gè)連桿上建立一個(gè)連桿坐標(biāo)系,。常用的方法是D-H (Denavit-Hartenberg)參數(shù)法，即使用矩陣方法來描述運(yùn)動(dòng)學(xué)問題,。只要已知各關(guān)節(jié)的D-H參數(shù),，就可根據(jù)正運(yùn)動(dòng)學(xué)公式A1A2A3A4A5A6=0T6得到機(jī)器人末端的位置和姿態(tài)［2］。

　　SA1400機(jī)器人各連桿坐標(biāo)系如圖1所示,，相鄰兩連桿n-1與n之間的相對關(guān)系能夠按照兩次旋轉(zhuǎn)和兩次平移的四次齊次變換來建立,，并把齊次變換矩陣記為An。此關(guān)系式為：

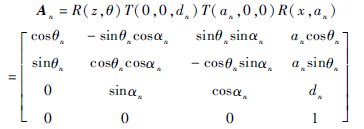
　　式中：θn為關(guān)節(jié)n的旋轉(zhuǎn)角度,，即兩連桿夾角,，符合右手定則為正；dn為關(guān)節(jié)n的偏距,，即兩連桿距離,；αn為關(guān)節(jié)n和n-1軸線之間的夾角，即連桿扭角,，符合右手定則為正；an為關(guān)節(jié)n和n-1軸線之間的公法線距離,，即連桿長度,，n=1,2,3…6［5］。D-H參數(shù)表如表1,。

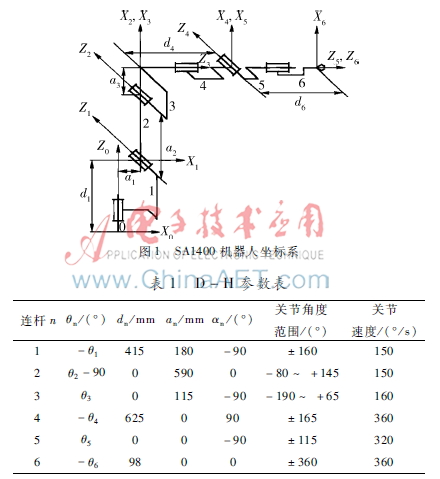
　　根據(jù)表1可得各變換矩陣如下：

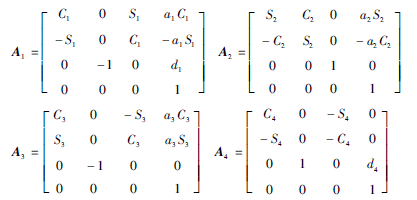
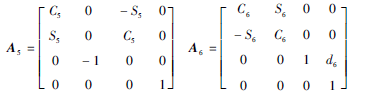
　　式中：Sn=sinθn,Cn=cosθn,下同,。所以末端執(zhí)行器的位姿方程為：

　　0T6=A1A2A3A4A5A6

　　2逆運(yùn)動(dòng)學(xué)方程的推導(dǎo)及求解

　　一般具有6個(gè)自由度的機(jī)器人沒有逆運(yùn)動(dòng)學(xué)封閉解，但某些特殊結(jié)構(gòu)的機(jī)器人還是可以得到多組封閉解的,，大多數(shù)工業(yè)機(jī)器人都可用Pieper提出的方法來求解,，這種方法是針對6個(gè)關(guān)節(jié)均為旋轉(zhuǎn)關(guān)節(jié)且后3個(gè)關(guān)節(jié)軸線相交的操作臂。此方法也可應(yīng)用于包括移動(dòng)關(guān)節(jié)的其他形式的操作臂,。觀察圖1中機(jī)器人,，其3、4、5關(guān)節(jié)的軸線Z3,、Z4,、Z5交于一點(diǎn)，因此,，這3個(gè)關(guān)節(jié)的運(yùn)動(dòng)不能產(chǎn)生沿Z2軸線方向的運(yùn)動(dòng),，所以這3個(gè)關(guān)節(jié)的變換矩陣乘積A3A4A5的第3行第4列上的元素為零。具有此特點(diǎn)的機(jī)器人,，其運(yùn)動(dòng)學(xué)逆解存在以下簡便求解方法［69］：

　　A3A4A5=A－12A－11TA－16(1)

　　等式左邊為

　　(1)求θ1

　　令式(1)左右兩邊矩陣的(3, 4)元素（表示矩陣的第三行第四列,，下同）相等，得：

　　S1(px－d6ax)+C1(py－d6ay)=0

　　則

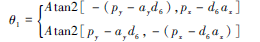
　　(2)求θ2

　　令式(1)左右兩邊(2, 4)和(1, 4)元素分別相等,，并化簡得：

　　a3C3-d4S3=-a2-C2v-S2u…①

　　a3S3+d4C3=-C2u+S2v……②(2)

　　式中：u=a1+C1(axd6－px)+S1(py－ayd6),，v=azd6－pz+d1，①②兩邊平方相加,，且令w=(d24+a23－a22－v2－u2)/(2a2),，得:

　　C2v+S2u=w

　　(6)求θ6

　　令式(1)左右兩邊(3, 2)元素相等，可得:

　　JC6－KS6=－C4

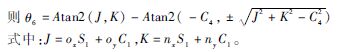
　　從以上各角度表達(dá)式可知,，逆解存在多解,，而控制機(jī)器人各關(guān)節(jié)的角度是唯一的。若忽略避障要求和軌跡優(yōu)化問題,，可按照以下步驟得到唯一解,。首先，如有必要,，將所得解加減360°,，以補(bǔ)出關(guān)節(jié)角度表達(dá)式值域沒有包含的其他可能解；其次,，由于關(guān)節(jié)運(yùn)動(dòng)范圍的限制,，應(yīng)舍去其中一些解（甚至全部）；最后,，根據(jù)“最短行程”原則,，選取一個(gè)最近解，使得每一個(gè)運(yùn)動(dòng)關(guān)節(jié)的移動(dòng)量最小,，以保證運(yùn)動(dòng)的連續(xù),、快速和低能耗，同時(shí)可用加權(quán)法使得解側(cè)重于移動(dòng)小連桿而不是移動(dòng)大連桿［8,，10］,。

　　3計(jì)算實(shí)例

　　已知空間中的A,B兩點(diǎn)，其位姿矩陣分別為：

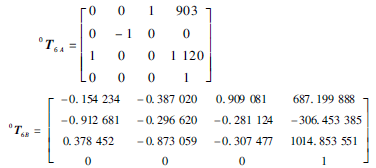
　　逆解得到A點(diǎn)各關(guān)節(jié)角度θ1~θ6依次為：0(180),0(83.12),0,0(90),0(0),0(0)（單位：度）,；B點(diǎn)6個(gè)關(guān)節(jié)角度依次為：25(-155),-15(89.60),20,-30(-150),15,-35(-93.29)（單位：度）,。括號中為該關(guān)節(jié)的第二個(gè)解,，本計(jì)算實(shí)例中假定各關(guān)節(jié)上一時(shí)刻的角度都為0度，則選取與0度的歐式距離較小的解為最優(yōu)解,。正解得到末端位姿分別為XA=903 mm,YA=0,ZA=1 120 mm,αA=0°,βA=-90°,γA=180°,；XB=687.2 mm,YB=-306.5 mm,ZB=1 014.9 mm,αB=-99.6°, βB=-22.2°,γB=-109.4°（α,β,γ為位姿坐標(biāo)系相對于機(jī)器人底座坐標(biāo)系或基坐標(biāo)系的RPY角）。計(jì)算結(jié)果表明,，本文中的正逆解方程是正確的,。

4運(yùn)動(dòng)學(xué)仿真

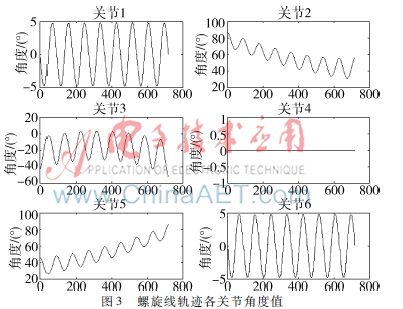
　　為驗(yàn)證本文正逆解方程的準(zhǔn)確性和可行性，使用MATLAB軟件對機(jī)器人走曲線軌跡的運(yùn)動(dòng)過程進(jìn)行仿真［11］,。仿真過程三維動(dòng)畫截圖與末端軌跡曲線如圖2,，圖中的理論軌跡與實(shí)際軌跡重合，說明本文正逆解方程是正確的,。運(yùn)動(dòng)過程中各關(guān)節(jié)角度值如圖3,，從圖中可知，運(yùn)動(dòng)過程中各關(guān)節(jié)角度值變化連續(xù),，且都在表1所列的關(guān)節(jié)角度范圍內(nèi),，說明本文所解方程是可行的，具有實(shí)用性［12］,。

5結(jié)束語

　　本文采用DH參數(shù)法建立了STEPSA1400型機(jī)器人的連桿坐標(biāo)系,，確定了該型機(jī)器人的DH參數(shù)及連桿間的位姿變換矩陣，求出了正運(yùn)動(dòng)學(xué)方程,。針對3個(gè)相鄰軸相交于一點(diǎn)的6自由度操作臂,，在研究總結(jié)了三軸相交的Pieper解法后，使用了一種避免大量矩陣逆乘運(yùn)算的逆解方法,?？紤]到三角函數(shù)的取值范圍和機(jī)器人各關(guān)節(jié)角之間的影響，角度值方程采用了雙變量反正切函數(shù),，通過自變量的符號確定關(guān)節(jié)角度所在的象限,，進(jìn)而取得合理解。針對逆解過程中出現(xiàn)的多解問題,，采用基于歐氏距離的“最短行程”原則選取最優(yōu)解,。為了驗(yàn)證所求解方程的準(zhǔn)確性和可行性，使用MATLAB進(jìn)行了運(yùn)動(dòng)學(xué)仿真,，仿真過程較真實(shí)地模擬了實(shí)際機(jī)器人的運(yùn)動(dòng)情況，仿真結(jié)果達(dá)到預(yù)期目標(biāo),。本文為該型機(jī)器人的應(yīng)用及其動(dòng)力學(xué)與控制器的研究打下基礎(chǔ),，同時(shí)，也為其他六自由度機(jī)器人運(yùn)動(dòng)學(xué)分析提供參考,。

參考文獻(xiàn)

　?。?］ 中國測控網(wǎng).工業(yè)4.0時(shí)代:工業(yè)機(jī)器人行業(yè)發(fā)展機(jī)遇分析［EB/OL］.(20151202)［20151204］ http://www.ck365. cn/wap/index.php?mid=21&itemid=39875.

　?。?］ 韓建海.工業(yè)機(jī)器人（第三版）［M］.武漢:華中科技大學(xué)出版社,2015.

　　［3］ 王其軍,杜建軍.MOTOMAN機(jī)器人逆運(yùn)動(dòng)學(xué)新分析［J］.哈爾濱工業(yè)大學(xué)學(xué)報(bào),2010,42(3):451454．

　?。?］ 王雪松,許世范,郝繼飛.MOTOMAN機(jī)械手逆運(yùn)動(dòng)方程新的推導(dǎo)方法及求解［J］.中國礦業(yè)大學(xué)學(xué)報(bào),2001,30(1):7376.

　?。?］ 蔡自興.機(jī)器人學(xué)（第二版）［M］.北京:清華大學(xué)出版社,2009.

　　［6］ PAUL R, SHIMANO B, MAYER G. Differential kinematic control equations for simple manipulators［J］. IEEE Trans SMC,1981,11(6):449455.

　?。?］ PIEPER D, ROTH B. The kinematics of manipulaor under computer control［C］. Proceeding of the Second International Congress on Theory of Machines and Mechanisms,1969(2):159169.

　?。?］ CRAIG J J.機(jī)器人學(xué)導(dǎo)論(第三版)［M］.贠超，譯.北京:機(jī)械工業(yè)出版社,2014.

　?。?］ 崔建國,宋愛國,黃惟一.遙操作系統(tǒng)中MOTOMANSV3機(jī)器人的運(yùn)動(dòng)建模研究［J］.東南大學(xué)學(xué)報(bào):自然科學(xué)版,2003,33(4):424429.

　?。?0］ 葉上高,劉電霆.機(jī)器人運(yùn)動(dòng)學(xué)逆解及奇異和多解的處理［J］.機(jī)床與液壓,2014,42(3):2729.

　　［11］ 林海峰,王姮.多關(guān)節(jié)機(jī)器人工作空間仿真方法［J］.微型機(jī)與應(yīng)用,2014,33(2):7274.

　?。?2］ 陳發(fā)堂,牛勇清,韓娜娜,等.協(xié)議一致性測試平臺的搭建及仿真實(shí)現(xiàn)［J］.電子技術(shù)應(yīng)用,2014,40(4):137140.