李傳輝,，劉純武，黃芝平

　?。▏揽茖W技術(shù)大學 機電工程與自動化學院,，湖南 長沙 410073）

　　摘要：在100G以太網(wǎng)媒體接入控制器（Media Access Control，MAC）的設計中,，需要采用高位寬的并行數(shù)據(jù)來降低對時鐘的要求,。在使用并行循環(huán)冗余校驗(Cyclical Redundancy Check，CRC)時會有一個問題,，即需要計算CRC的數(shù)據(jù)域長度不一定是數(shù)據(jù)通道位寬的整數(shù)倍,，導致最后一組數(shù)據(jù)無法使用數(shù)據(jù)通道的位寬對其進行CRC計算。為了解決這個問題,，本文提出了在幀前填充0的處理方法,。仿真和測試結(jié)果都驗證了該方法的可行性。該處理方法也能應用到其他的通信系統(tǒng)中,。

　　關(guān)鍵詞：100G以太網(wǎng),；并行CRC；高位寬

0引言

　　IEEE在2010年發(fā)布了40/100G以太網(wǎng)標準［1］,，其中MAC層仍然沿用以前的規(guī)定未作大的改變,，只是100 Gb/s的高速率使得無法沿用以前的方法完成CRC值的計算，為此,，本文提出了一種簡單有效的解決方法,。

1循環(huán)冗余校驗

　　在數(shù)字通信系統(tǒng)中，為了確保接收到的數(shù)據(jù)與發(fā)送端的數(shù)據(jù)一致,，需要引入差錯控制機制,。循環(huán)冗余校驗碼由于其誤碼監(jiān)測能力強,，抗干擾能力優(yōu)異，被廣泛應用于線路檢錯,。循環(huán)冗余檢驗是一種系統(tǒng)的縮短循環(huán)碼,，它采用多項式編碼方法［2］。設被檢驗的信息碼有n位,，信息系列M={mn-1 mn-2…m0},，用多項式M(x)可表示為：

　　M(x) = mn-1 xn-1 + mn-2 xn-2 + … + m1x1 +m0x0（1）

　　發(fā)送方和接收方使用同一個生成多項式G(x)，其是一個k階的二進制多項式,，而且G(x)的首位和最后一位的系數(shù)都必須是1,，其通用表達式為：

　　G(x)=xk+gk-1xk-1+gk-2xk-2+…+g1x+1（2）

　　CRC的計算規(guī)則為發(fā)送方以xk·M(x)除以生成多項式G(x)，將得到的余數(shù)R(x)作為校驗值,，這里的計算規(guī)則都是使用二進制運算規(guī)則,，R(x)可表示為：

　　R(x)=CRC(M(x))= xk·M(x)mod G(x)（3）

　　發(fā)送方將CRC值隨數(shù)據(jù)一起發(fā)送給接收方，接收方對接收到的數(shù)據(jù)進行CRC值的計算,，并將它與發(fā)送方的CRC值進行比較,。如果數(shù)據(jù)傳輸過程中沒有錯誤，兩者的校驗值就會是一致的,，相反如果得到的校驗值不一致,，就可以判斷出數(shù)據(jù)在傳輸過程中發(fā)生了錯誤，這時接收方就可以丟棄當前數(shù)據(jù)或要求發(fā)送方重傳數(shù)據(jù),。CRC校驗可以百分百地檢測出所有的奇數(shù)個的隨機錯誤和長度小于等于k的突發(fā)錯誤,。

2100G以太網(wǎng)的CRC設計

　　在以太網(wǎng)通信中，CRC校驗具有重要作用,。依據(jù)IEEE802.3以太網(wǎng)的幀格式（如圖1所示）,，CRC計算的數(shù)據(jù)區(qū)域包括目的地址、原地址,、長度/類型和負載數(shù)據(jù)圖1以太網(wǎng)幀格式區(qū)域,。得到的CRC值作為幀校驗序列（Frame Check Sequence，F(xiàn)CS）填充在數(shù)據(jù)幀尾,。其中規(guī)定了以太網(wǎng)幀F(xiàn)CS字段的生成算法為CRC32,，其生成的多項式表達式為：

　　G(x)=x32+x26+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1（4）

　　在吉比特以上速率的通信系統(tǒng)中，傳統(tǒng)的串行CRC校驗方法已無法滿足要求,，所以現(xiàn)在有很多新型并行CRC計算方法［35］,。因此在100G以太網(wǎng)中，其CRC也必須采用并行方法,，CRC計算的并行位寬就是數(shù)據(jù)通道的位寬,。提高數(shù)據(jù)位寬可以降低系統(tǒng)的時鐘頻率，但另一方面隨著并行數(shù)據(jù)位寬的增加會使得CRC電路的延遲時間增加,，影響系統(tǒng)的時序性能,。經(jīng)過綜合考慮本文中設計的數(shù)據(jù)并行位寬為320,。

　　使用320位的高并行位寬會使得數(shù)據(jù)的處理變得復雜。比如在MAC層的發(fā)送方,，上層客戶每個時鐘就會有一組320位40 B的數(shù)據(jù)送給MAC處理,，CRC模塊就會使用320位的并行算法對其計算。當前的CRC值只與上一次數(shù)據(jù)得到的CRC值及當前的數(shù)據(jù)有關(guān),，CRC值初始化為全0,，如圖2所示。

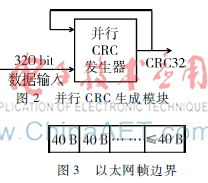
　　問題是數(shù)據(jù)并不一定是40 B的整數(shù)倍關(guān)系,，最后一組數(shù)據(jù)可能結(jié)束于任意位置,，如圖3所示。

　　在10G以太網(wǎng)中,，數(shù)據(jù)位寬為64 bit,，在參考文獻［6］中對這種情況的處理方法為同時設計從8 bit到64 bit的CRC生成模塊，根據(jù)有效字節(jié)數(shù)選擇使用其中一個,。這一方法無疑會占用大量資源，而且利用率低,。在100G以太網(wǎng)中數(shù)據(jù)位寬如果按320設計,，需要多達40個不同的CRC模塊，加上一個40路的多選一電路,，這樣的電路在資源使用和時序性能方面都是很糟糕的,。所以這一方法無法用于100G以太網(wǎng)中。文獻［7］中提到了一種級聯(lián)結(jié)構(gòu)可以計算任意字節(jié)的CRC,，但此結(jié)構(gòu)有個很明顯的缺點,，即級聯(lián)越大，電路延遲線性增加,，320位就需要級聯(lián)40次,，這樣的電路無法滿足時序要求。文獻［2］中利用了CRC校驗具有的Magic Number特性,，在數(shù)據(jù)幀后面添加0,，使得可以只用一個64 bit的CRC模塊完成接收方的CRC校驗，但無法在數(shù)據(jù)發(fā)送方完成CRC值的計算,。

3幀前補0的并行CRC

　　上節(jié)提到的10G以太網(wǎng)CRC的處理方法都無法直接應用于100G以太網(wǎng)中,。下面說明本文提出的方法：幀前補0后再進行CRC計算。

　　假設原始序列M有n位數(shù)據(jù),，n不是320位的整數(shù)倍,。i是一個小于320的整數(shù)，且i+n為320的整數(shù)倍,，在M前增加i個0構(gòu)造為新序列M′：

　　M′(x)=0·xi+n-1+…+0·xn+M(x)=0+M(x)=M(x)（5）

　　可以看出新序列在數(shù)值上與原來的序列值是一樣的,。這個很好理解,，就像在十進制中在最前面添加任意位數(shù)的0并不會改變這個數(shù)的數(shù)值一樣，當然這在二進制數(shù)當中同樣適用,。新序列的數(shù)據(jù)長度成為了320的整數(shù)倍,。

　　由CRC的計算公式（3）來看，CRC的結(jié)果只與序列的數(shù)值有關(guān),，所以用新序列計算CRC會得到與用原始數(shù)列同樣的結(jié)果,。所以依據(jù)此原理，只需要設計一個320位的并行CRC模塊,，計算時使用新的序列送給CRC模塊,，這個方法可以計算任意字節(jié)數(shù)據(jù)幀的CRC值。

　　假設有一幀數(shù)據(jù)負載字節(jié)長度為len,，加上目的地址,、源地址和數(shù)據(jù)/類型字段的長度14 B，則該幀需要參與CRC計算的數(shù)據(jù)總長為L=len+14,。令n=ceil(L/40),，ceil函數(shù)得到的是大于等于L/40的最小整數(shù)。令rem=mod(L,40)為L/40的余數(shù),，表示最后一組數(shù)據(jù)中有效數(shù)據(jù)的字節(jié)數(shù),，對應的com=40-rem表示無效的字節(jié)數(shù)，V=8*com則表示無效的比特數(shù),，也就是需要在幀前添加的0的比特個數(shù),。

　　在客戶端向MAC發(fā)送數(shù)據(jù)時，每個時鐘MAC層會收到一組數(shù)據(jù)Cur_data_in［319:0］,，設計一組初始化為全0的寄存器Last_data_in［319:0］用來保存上一時鐘的數(shù)據(jù),。根據(jù)V值的大小將Cur_data_in和Last_data_in組合成一組新的數(shù)據(jù)Data_to_crc［319:0］，其組合關(guān)系為：

　　Data_to_crc［319：0］=Last_data_in［V-1：0］&Cur_data_in［319：V］（6）

　　“&”表示并置連接,，處理過程如圖4所示,。新的序列就是送給CRC模塊的數(shù)據(jù)，從圖中可以看到在原始數(shù)據(jù)的前面添加了V個比特0,。每組數(shù)據(jù)都可以使用320位的并行CRC進行處理,，而且最后得到的結(jié)果與使用原始數(shù)據(jù)一樣。

　　4測試及分析

　　使用硬件描述語言VHDL實現(xiàn)上述的處理過程,，并將程序下載到FPGA中進行測試,，綜合出來的結(jié)果表明該方法在面積使用和運行速度方面的效果都很好。測試時客戶端給出了一些不同長度的以太網(wǎng)幀,，使用Quartus II中的SignalTap工具對數(shù)據(jù)流進行采樣,。圖5是rem值為18的一幀數(shù)據(jù)的第一組數(shù)據(jù)，可以看到data_to_crc在cur_data_in前面添加了22個比特0，這是符合設計預期結(jié)果的,。圖6所示是該幀數(shù)據(jù)的最后一組數(shù)據(jù),，根據(jù)rem值，cur_data_in只有18 B的有效數(shù)據(jù),，所以data_to_crc也只取了其中的18 B有效數(shù)據(jù),，在CC處結(jié)束，此時的CRC值就是最終的FCS值為83ACF5C1,。

　　為了驗證該值的正確性,，使用8位并行CRC算法計算該幀的CRC值，在ModelSim平臺下進行了仿真,。結(jié)果如圖7所示,，可以看到計算完CC后CRC值為83ACF5C1，與前面的結(jié)果一致,，說明了該方法得到的結(jié)果是正確的,。

5結(jié)束語

　　由于100G以太網(wǎng)中會使用很高的并行數(shù)據(jù)位寬，但是數(shù)據(jù)幀中需要進行CRC計算的數(shù)據(jù)長度不一定是位寬的整數(shù)倍,，本文針對這個問題提出了一種新的處理方法,，并且通過了測試。該方法簡單有效,，能夠克服傳統(tǒng)方法的缺陷,，在性能上有很大的提升。雖然本文是以100G以太網(wǎng)的CRC32作說明,，該方法也能很容易地應用于其他的高速通信系統(tǒng)。

參考文獻

　?。?］ IEEE. IEEE Std. 802.3ba［S］. 2010.

　?。?］ 彭建輝. 10G以太網(wǎng)接口并行CRC校驗的一種簡化算法［J］．微計算機信息,2006，22(20)：213215.

　?。?］ STAVINOV E.A practical parallel CRC generation method ［J］. Circuit Cellar, 2010(234)：3845.

　?。?］ 畢占坤,張羿猛,黃芝平，等.基于邏輯設計的高速CRC并行算法研究及其FPGA實現(xiàn)［J］. 儀器儀表學報, 2007,，28(12)：22442249.

　?。?］ KENNEDY C E， MOZAFFARIKERMANI M.Generalized parallel CRC computation on FPGA［C］. Canadian Conference on Electrical and Computer Engineering (CCECE), 2015:107113.

　?。?］ 張友亮,，劉志軍，馬成海,等. 萬兆以太網(wǎng)MAC層控制器的FPGA設計與實現(xiàn)［J］.  計算機工程與應用, 2012,48(6):7779.

　?。?］ 劉昭,蘇厲,金德鵬,等.10G以太網(wǎng)系統(tǒng)中的并行CRC編解碼器的設計［J］. 電子技術(shù)應用, 2004,30(4)：4750.