頡斌,楊揚(yáng),王潔瑩
(北京科技大學(xué) 計(jì)算機(jī)通信工程學(xué)院,北京100083)
摘要:對(duì)于Web服務(wù)組合優(yōu)化的問(wèn)題,蟻群算法的求解主要是串行進(jìn)行,收斂時(shí)間長(zhǎng),容易收斂于非最優(yōu)解。在云計(jì)算環(huán)境中,將蟻群算法并行化,可對(duì)Web服務(wù)組合優(yōu)化問(wèn)題進(jìn)行分布式并行求解。根據(jù)多目標(biāo)優(yōu)化模型給出基于多信息素的蟻群算法,使用MapReduce并行編程框架對(duì)蟻群算法中最耗時(shí)的部分——螞蟻獨(dú)立求解的過(guò)程并行化,給出了使用MapReduce改進(jìn)的基于多信息素的蟻群優(yōu)化算法,有效地對(duì)Web服務(wù)組合進(jìn)行全局優(yōu)化,彌補(bǔ)傳統(tǒng)的蟻群算法求解過(guò)程的缺點(diǎn)。
關(guān)鍵詞:服務(wù)組合;服務(wù)組合優(yōu)化;蟻群算法
0引言
隨著云計(jì)算的發(fā)展,Web服務(wù)組合優(yōu)化問(wèn)題已經(jīng)成為了國(guó)內(nèi)外研究的熱點(diǎn)。現(xiàn)有優(yōu)化算法一般是啟發(fā)式算法。許多研究結(jié)果表明,蟻群優(yōu)化算法具有分布式計(jì)算、魯棒性好等優(yōu)勢(shì),但通常需要足夠的群落大小和足夠數(shù)量的迭代。隨著目標(biāo)問(wèn)題規(guī)模的增長(zhǎng),會(huì)導(dǎo)致計(jì)算效率低下。蟻群算法的求解主要是在集中式串行環(huán)境下,而在云計(jì)算環(huán)境中,利用云計(jì)算技術(shù)將蟻群算法并行化對(duì)問(wèn)題進(jìn)行分布式并行求解的研究較少。
大多數(shù)現(xiàn)有并行化的蟻群算法都依賴于使用傳統(tǒng)的并行編程模型來(lái)實(shí)現(xiàn)。MANFRIN M等人用消息傳遞接口(Message Passing Interface,MPI)在多機(jī)環(huán)境中實(shí)現(xiàn)了TSP的并行ACO [1]。CRAUS M等人用一種一主多從機(jī)制實(shí)現(xiàn)了基于MPI的并行ACO算法[2]。Huang Diwei等人用MapReduce實(shí)現(xiàn)了作業(yè)調(diào)度問(wèn)題的遺傳算法,并得到了合理的結(jié)果[3]。參考文獻(xiàn)[4]用MapReduce針對(duì)TSP實(shí)現(xiàn)了并行的蟻群算法,但存在多次迭代使算法性能降低的問(wèn)題。
本文提出將蟻群算法并行化的思想,使用MapReduce并行化編程模型,將基本的蟻群算法并行化,可解決云計(jì)算環(huán)境下使用蟻群算法進(jìn)行Web服務(wù)組合優(yōu)化容易出現(xiàn)的求解困難的問(wèn)題。本文根據(jù)多目標(biāo)優(yōu)化模型給出基于多信息素的蟻群算法,使用MapReduce并行編程框架對(duì)蟻群算法中最耗時(shí)的部分——螞蟻獨(dú)立求解的過(guò)程并行化,給出使用MapReduce改進(jìn)的基于多信息素的蟻群算法。
1問(wèn)題建模
1.1優(yōu)化目標(biāo)建模
本文選擇子服務(wù)的負(fù)載、服務(wù)級(jí)別協(xié)議[5](Service Level Agreement, SLA)(包括價(jià)格C(Si)、執(zhí)行時(shí)間T(Si)、可靠性A(Si))以及用戶優(yōu)先級(jí)這3個(gè)非功能性屬性約束條件來(lái)制定服務(wù)組合優(yōu)化的目標(biāo)準(zhǔn)則。利用排隊(duì)論思想,定義這些指標(biāo)為隨時(shí)間t變化而變化的密度分段函數(shù)。
(1)服務(wù)的負(fù)載
QB(Si)=λ/μ(1)
其中,λ為任務(wù)到達(dá)率,μ為服務(wù)率。
(2)服務(wù)級(jí)別協(xié)議(SLA)
本文選取3個(gè)服務(wù)質(zhì)量參數(shù):價(jià)格C(Si) 、執(zhí)行時(shí)間T(Si)、可靠性A(Si)。
服務(wù)的價(jià)格C(Si)表示為:
QC(Si)=C(2)
執(zhí)行時(shí)間T(Si)的密度函數(shù)為:
QT(Si)=p(T(Si))=(μ-λ)e-(μ-λ)t,t>0(3)
服務(wù)Si的可靠性A(Si)反映了服務(wù)的可靠程度,即單位時(shí)間內(nèi)服務(wù)可用的時(shí)間與服務(wù)的失效率成反比。出錯(cuò)率的分布函數(shù)為:
QA(Si)=p(A(Si))=βt,0<t<T(4)
其中,T為出錯(cuò)維護(hù)時(shí)間。
(3)用戶優(yōu)先級(jí)
L(Si)=l(5)
本文采用參考文獻(xiàn)[6]中的預(yù)處理方法,將這些非功能性屬性的值進(jìn)行標(biāo)準(zhǔn)化的轉(zhuǎn)換。設(shè)一個(gè)Web服務(wù)Sij,具有n個(gè)非功能性屬性,表示為Qij={q1ij,q2ij,…,qnij}。通過(guò)式(6)、式(7)進(jìn)行轉(zhuǎn)換。若第r個(gè)屬性為正屬性,則用式(6)處理;若第r個(gè)屬性為負(fù)屬性,則用式(7)處理。

其中,qrmax為組合服務(wù)中全部Web服務(wù)中第r個(gè)屬性中的最大值,∑qrml為組合服務(wù)中全部Web服務(wù)的第r個(gè)屬性之和。
1.2Web服務(wù)組合優(yōu)化問(wèn)題的建模
在Web服務(wù)組合優(yōu)化的過(guò)程中,對(duì)非功能性屬性簡(jiǎn)單地加和會(huì)影響某些屬性值,不能準(zhǔn)確地表達(dá)非功能性屬性[7]。通常將Web服務(wù)組合優(yōu)化問(wèn)題轉(zhuǎn)換成有限方案的多目標(biāo)決策問(wèn)題,在各目標(biāo)之間進(jìn)行協(xié)調(diào)權(quán)衡,使得所有目標(biāo)函數(shù)盡可能達(dá)到最優(yōu)。
將多目標(biāo)優(yōu)化問(wèn)題定義為一個(gè)三元組:(X,C,F)。其中X代表一個(gè)n維決策空間,即x=(x1,x2,…,xn)∈X;C代表一個(gè)集合,包含了一組決策變量所同時(shí)滿足的約束條件;F是一個(gè)矢量,包含所有的目標(biāo)函數(shù),個(gè)數(shù)m≥2,可表示為:F=(f1(x),f2(x),…,fm(x))。多目標(biāo)優(yōu)化就是使這些不同的目標(biāo)函數(shù)同時(shí)達(dá)到最小。當(dāng)多個(gè)目標(biāo)要同時(shí)達(dá)到最優(yōu)時(shí),最優(yōu)解就是Pareto最優(yōu)集。
設(shè)單個(gè)Web服務(wù)為Sij={Fij,Qij},其中Fij為功能性屬性集合。服務(wù)組合優(yōu)化問(wèn)題就是在由服務(wù)節(jié)點(diǎn)構(gòu)成的圖中的多條路徑中選擇一條,使得這條路徑中的各個(gè)非功能屬性的匯總能夠符合用戶需求[8]。這就將服務(wù)組合優(yōu)化的問(wèn)題轉(zhuǎn)換為了一個(gè)多目標(biāo)決策的數(shù)學(xué)問(wèn)題,即針對(duì)組合服務(wù)的多個(gè)非功能性目標(biāo)進(jìn)行優(yōu)化。本文考慮串行服務(wù)組合問(wèn)題。
(1)負(fù)載

利用式(6)和式(7)對(duì)服務(wù)的各個(gè)非功能性屬性進(jìn)行預(yù)處理。設(shè)這個(gè)組合服務(wù)中共包含m個(gè)子服務(wù)實(shí)例,候選服務(wù)實(shí)例共有n個(gè),則將Web服務(wù)組合優(yōu)化問(wèn)題轉(zhuǎn)換為多目標(biāo)優(yōu)化的數(shù)學(xué)模型,多目標(biāo)函數(shù)如式(13)所示。
f1=∑mi=1λiμi∑ni=1λiμi
f2=m(QCmax+1)∑ni=1Ci-1
f3=m(QTmax+1)τe-τt-1
f4=∑mi=1βit∑ni=1βit
f5=∑mi=1li∑ni=1li(13)
算法的目標(biāo)就是使式(13)中的5個(gè)目標(biāo)函數(shù)均盡量達(dá)到最小,此時(shí)所得到的Pareto最優(yōu)解集就是服務(wù)組合優(yōu)化后的解集。
2基于MapReduce改進(jìn)的蟻群算法
2.1多信息素蟻群算法
基本的蟻群算法是針對(duì)于單一種類信息素的,因而無(wú)法解決組合服務(wù)中多屬性約束的問(wèn)題。但本文是針對(duì)Web服務(wù)組合中的多個(gè)非功能性屬性進(jìn)行優(yōu)化,因此要對(duì)蟻群算法進(jìn)行改進(jìn)。在本文的改進(jìn)蟻群算法中,啟發(fā)式信息和信息素都用服務(wù)的多個(gè)非功能性屬性來(lái)表示,每個(gè)非功能性屬性都對(duì)應(yīng)一個(gè)目標(biāo)函數(shù)。
通常把信息素限制在一個(gè)區(qū)間,設(shè)為[τmin,τmax]。用于Web服務(wù)組合優(yōu)化的多信息素蟻群算法1如下所述:
算法1:多信息素蟻群算法
(1)所有信息素初始化都為τmax;
(2)設(shè)定目標(biāo)函數(shù)共為n個(gè),總的迭代循環(huán)次數(shù)為m;
(3)蟻群算法開(kāi)始,每只螞蟻開(kāi)始行動(dòng)。第j代螞蟻單獨(dú)選路時(shí),隨機(jī)選取一個(gè)優(yōu)化目標(biāo)函數(shù)(設(shè)為第i個(gè)),然后以第i個(gè)信息素表中的信息素求解一個(gè)解(求解方法見(jiàn)算法2);
(4)單獨(dú)選路完畢,即更新第i個(gè)信息素表中的所有信息素值;
(5)如果j=n,則計(jì)算結(jié)束,否則返回步驟(2)繼續(xù)計(jì)算。
2.2狀態(tài)轉(zhuǎn)移概率
將服務(wù)實(shí)體Sij的第k個(gè)非功能性屬性的信息素表示為τki(j),將第k個(gè)非功能性屬性的啟發(fā)式信息表示為ηki(j)。狀態(tài)轉(zhuǎn)移概率的計(jì)算公式如式(14)所示,其中α和β參數(shù)分別決定了信息素和啟發(fā)式信息的相對(duì)影響力。
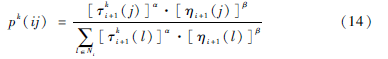
規(guī)定式(14)中的啟發(fā)式信息ηi(j)為用戶所關(guān)注的所有非功能屬性的啟發(fā)式信息(即n個(gè)優(yōu)化目標(biāo))之和,由式(15)求出。根據(jù)這個(gè)規(guī)則求解即可完成組合服務(wù)的多目標(biāo)優(yōu)化。利用這個(gè)轉(zhuǎn)移概率,基于多信息素的蟻群算法中螞蟻根據(jù)信息素求解的過(guò)程如下:
算法2:解的構(gòu)建算法
(1)初始化解為空;
(2)按照式(14)計(jì)算出下一子任務(wù)中所有子服務(wù)實(shí)體的轉(zhuǎn)移概率,選擇轉(zhuǎn)移概率最大的服務(wù)實(shí)體,更新解空間;
(3)如果所有任務(wù)都已選擇完成,則返回,否則轉(zhuǎn)到步驟(2)。
ηi(j)=∑nk=1ηki(j)(15)
2.3信息素更新規(guī)則
綜上所述,信息素更新規(guī)則總結(jié)如下:
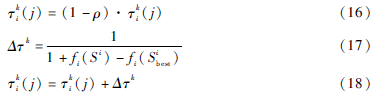
算法3: 信息素更新規(guī)則
(1)初始化i=1。
(2)首先按照式(16)求出新的第i個(gè)信息素表中的信息素值,范圍已設(shè)定為[τmin,τmax],若超過(guò),則取邊界值。
(3)利用目標(biāo)函數(shù)fi的公式計(jì)算出所有解的目標(biāo)函數(shù)值,根據(jù)式(17)求出Δτk,利用式(18)計(jì)算最新的信息素。更新后的信息素值若在[τmin,τmax]之外,則一律取邊界值。
(4)若解Si優(yōu)于解Sibest,則令Sibest=Si。
(5)若信息素表未被完全更新,則i增加1,算法跳轉(zhuǎn)到步驟(3);否則返回,更新信息素結(jié)束。
2.4MapReduce并行化改進(jìn)
本文為了使用蟻群算法解決多目標(biāo)優(yōu)化的問(wèn)題并減少計(jì)算量,將基于多信息素的蟻群算法進(jìn)行并行化的改進(jìn)。在云計(jì)算環(huán)境下,引入MapReduce思想,改進(jìn)蟻群算法,應(yīng)用Map函數(shù)來(lái)并行化每只螞蟻的獨(dú)立求解過(guò)程,用Reduce函數(shù)分解出問(wèn)題的解和值,求得較優(yōu)解并處理信息素更新。從整體結(jié)構(gòu)上,應(yīng)用云計(jì)算的管道能力實(shí)現(xiàn)逐代的計(jì)算。具體設(shè)計(jì)如下:將多個(gè)Map、Reduce函數(shù)首尾相連,本代任務(wù)的輸出作為下一代任務(wù)的輸入,開(kāi)始下一個(gè)并行計(jì)算任務(wù)。將多對(duì)Map、Reduce任務(wù)串行起來(lái),形成一個(gè)Map1Reduce1Map2Reduce2…MapnReducen的執(zhí)行序列。
3仿真實(shí)驗(yàn)
本實(shí)驗(yàn)以校園云平臺(tái)為背景、以平臺(tái)上的服務(wù)組合實(shí)例為基礎(chǔ)進(jìn)行。組合服務(wù)實(shí)例共有5個(gè)子任務(wù),將每個(gè)子任務(wù)上部署10個(gè)服務(wù)實(shí)例。實(shí)驗(yàn)部署在Apache Hadoop 0.21.0環(huán)境中,MapReduce集群包含了16個(gè)節(jié)點(diǎn)。實(shí)驗(yàn)中螞蟻數(shù)=100,循環(huán)次數(shù)n=2 000,集群中計(jì)算機(jī)數(shù)目=2。其他參數(shù)取值為:τmin=10,τmax=100,ρ=0.01,啟發(fā)式信息按照式(15)取值,信息素按算法3進(jìn)行迭代更新。
3.1算法優(yōu)化效果測(cè)試
每輪測(cè)試10次,取平均數(shù)。針對(duì)兩種情況進(jìn)行對(duì)比實(shí)驗(yàn):α=2,β=2;α=1,β=4,輸出結(jié)果如圖1、圖2所示。圖中縱軸代表各個(gè)目標(biāo)函數(shù)的結(jié)果的平均值。
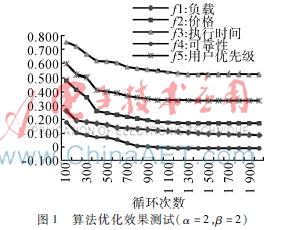
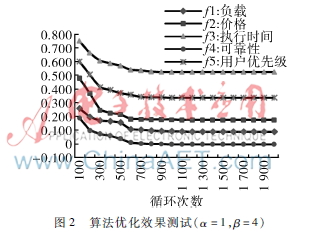
由圖1、圖2可見(jiàn),5個(gè)目標(biāo)函數(shù)隨著循環(huán)次數(shù)增加全部呈減小趨勢(shì),并且在一定的循環(huán)次數(shù)時(shí)趨近于穩(wěn)定值。圖2中目標(biāo)函數(shù)收斂得更快一點(diǎn),可見(jiàn)通過(guò)改進(jìn)的蟻群算法,使得服務(wù)組合得到了有效優(yōu)化。第二組參數(shù)取值中,β取值較大,說(shuō)明螞蟻在選路時(shí),受到啟發(fā)式信息的影響更大,所以目標(biāo)函數(shù)收斂速度更快。
上述實(shí)驗(yàn)證明了本文算法的有效性,結(jié)果穩(wěn)定且有良好的魯棒性。
3.2MapReduce并行化效率提升測(cè)試
本實(shí)驗(yàn)中,算法連續(xù)運(yùn)行10次,對(duì)運(yùn)行時(shí)間取平均值,結(jié)果如圖3所示。其中橫坐標(biāo)是MapReduce并行化節(jié)點(diǎn)job個(gè)數(shù),縱坐標(biāo)是運(yùn)行時(shí)間(ms)。
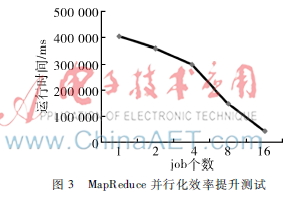
由圖3可見(jiàn),折線圖呈近線性下降趨勢(shì),表明該并行化方法達(dá)到了近線性的加速優(yōu)化,說(shuō)明基于MapReduce對(duì)蟻群算法中最耗時(shí)的螞蟻獨(dú)立求解部分進(jìn)行并行化,有效提高了優(yōu)化效率。
4結(jié)論
本文改進(jìn)了傳統(tǒng)的蟻群算法,增加多信息素,使其適用于多目標(biāo)優(yōu)化的數(shù)學(xué)問(wèn)題,同時(shí)考慮到蟻群算法的隱含并行性質(zhì),利用MapReduce框架將算法中最耗時(shí)的螞蟻獨(dú)立求解過(guò)程并行化。根據(jù)制定好的目標(biāo)準(zhǔn)則,使用改進(jìn)過(guò)的蟻群算法對(duì)云計(jì)算環(huán)境下的Web服務(wù)組合進(jìn)行有效的全局性優(yōu)化。通過(guò)仿真實(shí)驗(yàn)驗(yàn)證了方法的有效性。
參考文獻(xiàn)
[1] MANFRIN M, BIRATTARI M, STTZLE T, et al. Parallel multicolony ACO algorithm with exchange of solutions[C]. BelgiumNetherlands Conference on Artificial Intelligence, 2006.
[2] CRAUS M, RUDEANU L. Parallel framework for antlike algorithms[C]. 2004 Third International Symposium on Parallel and Distributed Computing, 2004 Third International Workshop on Algorithms, Models and Tools for Parallel Computing on Heterogeneous Networks, IEEE, 2004:3641.
[3] Huang Diwei, Lin Jimmy. Scaling populations of a genetic algorithm for job shop scheduling problems using MapReduce[C]. Proceedings of the 2010 IEEE Second International Conference on Cloud Computing Technology and Science, IEEE Computer Society, 2010:780785.
[4] 夏衛(wèi)雷,王立松.基于MapReduce的并行蟻群算法研究與實(shí)現(xiàn)[J].電子科技,2013, 26(2):146149.
[5] 徐忠勝,沈蘇彬.一種云計(jì)算資源的多目標(biāo)優(yōu)化的調(diào)度方法[J].微型機(jī)與應(yīng)用, 2015,34(13):1720.
[6] 劉彬,張仁津.基于QoS多目標(biāo)優(yōu)化的Web服務(wù)組合方法[J].計(jì)算機(jī)工程與設(shè)計(jì),2012, 33(3):885889.
[7] AKBAR M M, MANNING E G, SHOJA G C, et al. Heuristic solutions for the multiplechoice multidimension knapsack problem[M]. Computational Science ICCS 2001. Springer Berlin Heidelberg, 2001:659668.
[8] WADA H, SUZUKI J,YAMANO Y, et al. E3: a multiobjective optimization framework for SLAaware service composition[J]. IEEE Transactions on Services Computing, 2012, 5(3):358372.

