《電子技術應用》
您所在的位置：首頁 > 通信與網絡 > 設計應用 > 基于非線性海面微波段多普勒回波的建模算法
基于非線性海面微波段多普勒回波的建模算法
2016年電子技術應用第5期
陳澤宗1,，2,，張雨薇1，趙 晨1,，張龍剛1,，陳 曦1
1.武漢大學 電子信息學院，湖北 武漢430072,；2.武漢大學 地球空間信息技術協同創(chuàng)新中心,，湖北 武漢430079
摘要： 基于線性波浪理論和尖波模型，分別仿真得到時變線性和非線性海面,，并比較了不同海況下兩種海面模型的統計特征,。采用小斜率近似法求解微波段的電磁散射，并分析了不同條件下的回波多普勒譜。通過采用海浪反演算法驗證仿真數據,，證明了該建模算法的正確性,。結果表明，非線性海浪表現出斯托克斯波浪的典型特性,，海面的非線性效應在掠入射時對多普勒譜的影響更顯著,，并且進行了非線性修正的海面模型的電磁散射特性與實際海況的結果更加吻合。
中圖分類號： TN015
文獻標識碼： A
DOI：10.16157/j.issn.0258-7998.2016.05.027
中文引用格式： 陳澤宗,，張雨薇,，趙晨，等. 基于非線性海面微波段多普勒回波的建模算法[J].電子技術應用,，2016,，42(5)：97-100.
英文引用格式： Chen Zezong，Zhang Yuwei,，Zhao Chen,，et al. Modeling algorithm of microwave band Doppler echo based on nonlinear sea[J].Application of Electronic Technique，2016,，42(5)：97-100.
Modeling algorithm of microwave band Doppler echo based on nonlinear sea
Chen Zezong1,，2，Zhang Yuwei1,，Zhao Chen1,，Zhang Longgang1，Chen Xi1
1.School of Electronic Information,，Wuhan University,，Wuhan 430072，China,； 2.Collaborative Innovation Center for Geospatial Technology,，Wuhan University，Wuhan 430079,，China
Abstract： Based on linear wave theory and Choppy Wave Model, this paper simulates linear and nonlinear dynamic sea surface, and compares the statistical characteristics of two ocean models under different sea conditions. Using small slope approximation method to solve the issue of microwave electromagnetic scattering, the article analyzes the echo Doppler spectrum with different factors. By using wave inversion algorithm to verify the simulation data, the modeling algorithm is proved to be correct. Results show that nonlinear waves have typical characteristics of Stokes waves, and nonlinear effects have a more significant influence on doppler spectrum at grazing incidence. The electromagnetic scattering of ocean surface added with nonlinear features are more consistent with sea surface conditions.
Key words : nonlinear sea waves,；time-evolving ocean surface；small slope approximation,；microwave scattering fields,；Doppler spectrum

0 引言

    海表面電磁散射問題的研究在微波遙感、環(huán)境監(jiān)測及海上目標識別等領域中有重要意義和價值,。以往的研究通常把海面近似為簡單的線性模型,，但實際海浪的非線性特征會對海面的散射回波產生重要影響。

    目前,，國內外很多學者對時變非線性海面的電磁散射問題展開了大量研究。文獻[1]將海面高度和潛在的速度矢量表示成一對規(guī)范的哈密頓函數，提出了“改進的線性模型”,。文獻[2]提出了尖波模型,，其在海面電磁散射特性的研究中得到了廣泛應用。文獻[3]提出小斜率近似模型,，它構造出滿足互易性的冪級數展開式,。文獻[4]通過引入海浪的二階譜來反映波面的不對稱性，研究了非高斯表面分布的海面的后向散射系數,。

    本文在線性海面建模的基礎上,，引入尖波模型進行修正，得到非線性海浪的形態(tài)特征及統計特性,。采用小斜率近似法研究了兩種海面模型在不同條件下的電磁散射問題并模擬出微波段的回波多普勒譜,。結果直觀地反映了海面的非線性特征對微波段雷達回波的影響。

1 線性與非線性海面建模

1.1 線性海面建模

    海浪譜反映了海浪的能量在空間頻率上的分布,，本文采用Pierson-Moskowitz譜,，其表達式為：

    tx1-gs1.gif

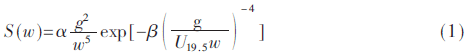
式中，α=8.1×10-3,，β=0.74,， w為海浪角頻率，U19.5是海面上方19.5 m處的風速,，g為重力加速度,。

    根據線性波浪理論，某一時刻的波面位移為一系列不同振幅,、頻率及初始相位的余弦波的疊加,。本文采用雙疊加法來建立線性海面模型，可得到波面位移為：

    tx1-gs2.gif

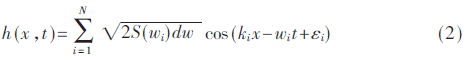
其中,， x表示海面離散點的位置,， t為時間， N是頻率上的離散點數,，wi為角頻率,，ki為波數，εi取0~2π內分布的隨機相位,。

1.2 非線性海面建模

    由于海浪的非線性作用,，實際海面的形態(tài)以及統計參量與簡單的線性海面模型不同，而這種非線性特征會對微波段的電磁散射產生重要影響,。在各種非線性理論分析中,，尖波模型(Choppy Wave Model，CWM)有便于計算的解析形式,。該模型對t時刻線性海浪的波面位移進行希爾伯特變換,，計算得到海面水平方向位移的增量：

tx1-gs3-4.gif

2 電磁散射計算

    小斜率近似方法(Small Slope Approximation,，SSA)由VORONOVICH A提出[5]，其綜合了基爾霍夫近似方法和微擾法,，適合計算具有復合尺度粗糙度的海面散射問題,。故本文采用一階小斜率近似方法。

    微波段電磁波入射到長度為L的海面z=h(x,，t)上,，時變海面的散射幾何模型如圖1所示。入射波矢量為Ki,，散射波矢量為Ks,，θi和θs分別為入射角和散射角。

tx1-t1.gif

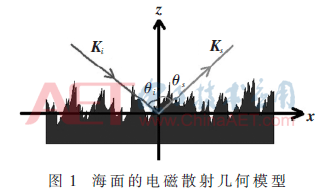
    根據圖1中的幾何關系,，入射波矢量和散射波矢量可表示如下：

    tx1-gs5.gif

式中,，k0和qi分別為入射波矢量投影到x軸和z軸的分量，k1和qs分別為散射波矢量投影到x軸和z軸的分量,。

    由于仿真的海面長度有限,，可能會在掠入射時產生較強的邊緣繞射現象，導致后向散射系數的計算出現偏差,。為了消除這種影響,，本文采用錐形平面波作為入射場，其表達式如下,。其中,，ki為入射電磁波波數，θi為入射角,，g是錐形波的波束寬度因子,。

     tx1-gs6.gif

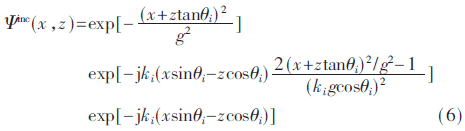
    根據SSA中散射振幅的不變性可以推導得到散射振幅的表達式為：

     tx1-gs7.gif

式中，Pinc為入射波的功率,，B(k0,，k)為根據極化方式取值的一階散射系數矩陣[6]。將海水當作理想導體對其進行簡化,，得到不同的極化方式可表示如下[7],。其中，Bvv表示垂直極化方式,，BHH表示水平極化方式,。

tx1-gs8-10.gif

    多普勒譜可以由散射振幅S(k0，k1,，t)推導得到：

    tx1-gs11.gif

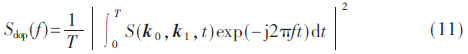
3 數值結果分析

3.1 線性與非線性海面的統計特性對比

    圖2表示某一時刻線性和非線性海面的波面位移的對比,。U10=10 m/s，海面長度取200 m,。取T=0.5 s時刻,，橫軸是海面的水平距離,，縱軸表示波面位移。分析圖2可以看出,，非線性海浪是波谷相對較平緩而波峰較陡峭的非對稱曲線,。這與斯托克斯波理論相符合，是非線性海浪的一個重要表現特征,。

tx1-t2.gif

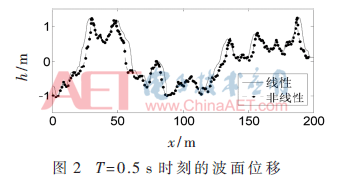
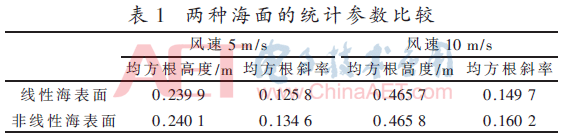
    表1是取不同風速時線性海浪和非線性海浪高度的均方根及斜率的均方根的對比。分析下表可知,，隨著風速增加,，海面的波面位移變大，斜率也增大,，說明海面的粗糙度變大,。并且兩者的均方根高度差別不大，但是非線性海浪的均方根斜率明顯比線性海面略大,。

tx1-b1.gif

    海面大尺度的斜率分布反映了海面的粗糙程度,，而海面的電磁散射會受其影響。圖3中的(a)和(b)分別給出了取T=0.5 s時刻圖2中兩種海面斜率的概率密度函數（Probability Density Function,，PDF）和累積分布函數（Cumulative Distribution Function,，CDF）。通過比較可知,，線性海浪的斜率分布是高斯的,，而非線性海浪的斜率分布與高斯分布有偏差。并且線性海面的斜率集中在較小值,，分布較為平均,，而尖波模型得到的非線性海面更容易出現特別大和特別小的斜率。

tx1-t3.gif

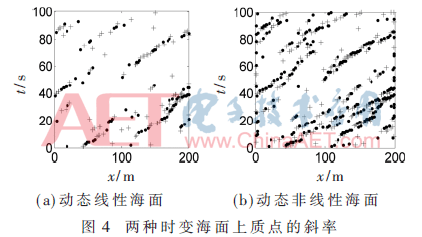
    為了便于觀察時變線性和非線性海面上離散點的斜率隨時間的變化趨勢,，可以把斜率超過0.3的質點用點標示（·）出來,，斜率低于-0.3的質點用加號（+）標示。如圖4所示,，時間取100 s,，其他仿真參數同上。橫軸表示海面的水平距離,，縱軸表示海面斜率隨時間的變化,。由圖可知，非線性海面的斜率取值變化更大,。相較于線性海面,，動態(tài)非線性海面上具有較大斜率的質點數量有所增加，而且斜率較小的質點數量也明顯更多,。

tx1-t4.gif

3.2 多普勒譜對比分析

    入射電磁波頻率取f=2.85 GHz,，海面上方10 m處風速取5 m/s,。海面長度L取200 m，入射角設為60°,，入射錐形波的波束寬度因子g取L/6,，后向散射取θs=-θi，用水平極化方式,。時變海面的時間間隔取0.007 8(1/128) s,，時間離散點數設為512，計算這4 s內時變海面的電磁散射,，多普勒譜的頻率分辨率為0.125 Hz,。圖5表示基于時變線性海面模型與尖波模型計算得到的多普勒譜。從下圖可以看出,，非線性海面的回波多普勒譜的譜寬稍大一些,，可能因為考慮了海面的非線性效應后，海面波浪的運動速度變快,。

tx1-t5.gif

    入射角取0~90°,，其他仿真條件同上，海面散射計算的樣本數為100,。從圖6(a)可知,，當電磁波近似垂直入射時，海面的鏡面散射機制起主導作用,，產生的回波功率較大,，因此后向散射系數也較大，并且兩者的后向散射系數沒有區(qū)別,。當入射角變大時,，布拉格共振散射變強，鏡面散射減弱,，回波功率變小,，因此后向散射系數變小，并且非線性海面的后向散射系數略大,。觀察圖6(b)可知,，對于兩種不同的海面模型，入射角較小時,，海面主要是鏡面散射,，多普勒頻移很小,；隨著入射角變大,，海面的布拉格共振散射變強，頻移快速增加,；而當入射角增大至掠入射時,，頻移增加的趨勢變慢,，并且非線性海面的頻移較大。

tx1-t6.gif

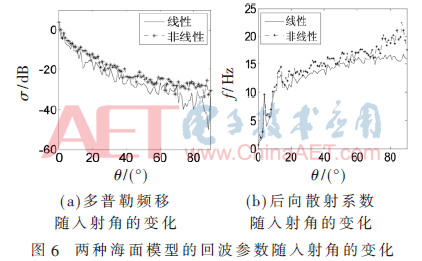
4 基于仿真數據的海浪反演算法驗證

4.1 多普勒譜建模

    取t=0.5 s時刻,，十米風速取10 m/s,，風向角設為0°，海面長度取200 m,，距離取200 m,。x軸為海面水平長度，y軸為海面距離,，z軸為海表面高度起伏,。圖7給出了基于雙疊加法生成的線性海面三維幾何模型。

tx1-t7.gif

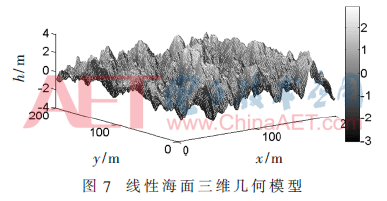
    入射波頻率設為2.85 GHz,，入射角取0°，用水平極化方式,，其他條件同上,。以0.003 9 s的時間間隔讓圖7生成一系列動態(tài)海面，每0.5 s（即128個時間點）構成一個多普勒譜,，時間長度取128 s,，由連續(xù)的動態(tài)海面生成256個多普勒譜樣本。圖8為128 s內得到的256個時間多普勒譜,。橫軸為頻率,，縱軸為時間。再根據本文的算法生成非線性海面的回波多普勒譜,。

tx1-t8.gif

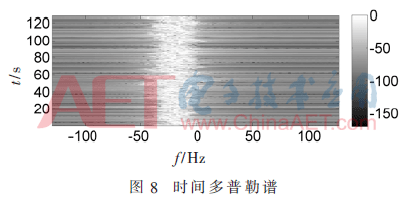
4.2 基于建模數據的海浪反演算法驗證

    根據經典的功率譜估計方法求得多普勒譜的中心頻率,，再由多普勒譜頻移計算得到徑向速度序列和速度譜。從建模得到的線性和非線性多普勒譜中求得的速度序列如圖9所示,，該速度序列的時間分辨率為0.5 s,，共256個數據點，總時長為128 s,，由圖可知,，速度序列呈現出很好的海浪起伏特征。

tx1-t9.gif

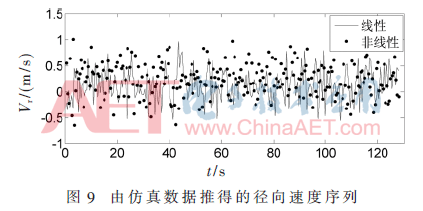
    采用海浪反演算法由徑向速度譜推導得到海浪譜,，并對其進行海浪參數提取,。圖10為根據海浪反演算法提取的海浪譜，由圖可知,，非線性海面建模計算出的回波多普勒譜反演誤差較小,，與實測數值更接近。

tx1-t10.gif

5 結語

    本文在時變線性海面和CWM非線性海面建模的基礎上,，對比了線性海面模型和非線性海面模型的統計特性,，所建立的海面模型基本反映了海況的變化特征,。采用一階小斜率近似方法分析了微波電磁波與海表面的電磁散射問題，然后通過仿真得到了微波雷達的回波多普勒譜,，表現了海面的非線性效應對回波多普勒頻譜的影響,。通過對仿真數據進行海浪反演算法的驗證，證實了該仿真模型的有效性,。結果表明,，進行了非線性修正的海面模型包含了更多海面幾何結構的信息，且其電磁散射特性與實際海況的結果更加吻合,。仿真得到的多普勒譜信噪比高,，不受海浪破碎以及存在目標等因素影響。該算法真實反映了海面非線性特征對微波段回波多普勒譜的影響,，其結論有助于分析實測數據中非線性效應對海浪參數反演結果的影響,，具有重要的指導意義。

參考文獻

[1] CREAMER D B,，HENYEY F,，SCHULT R，et al.Improved linear representation of ocean surface waves[J].Journal of Fluid Mechanics,，1989,，20(5)：135-161.

[2] NOUGUIER F，GU?魪RIN C,，CHAPRON B.“Choppy wave” model for nonlinear gravity waves[J].Journal of Geophysical Research Oceans,，2009，114(C9)：C09012-C09027.

[3] VORONOVICH A.Small-Slope approximation for electro-magnetic wave scattering at a rough interface of two dielectric half-spaces[J].Waves in Random Media,，1994,，4(3)：337-367.

[4] 侯海平，張本濤,，陳標.基于二階譜的海面微波散射特性仿真[J].青島大學學報：自然科學版,，2006(2)：24-27.

[5] VORONOVICH A.Wave scattering from rough surfaces[J].Springer Berlin，2012,，89(2)：529-541.

[6] 劉偉.二維粗糙地海面極化電磁散射的相關問題研究[D].西安：西安電子科技大學,，2013.

[7] VORONOVICH A.Small-slope approximation for electro magnetic wave scattering at a rough interface of two dielectric half-spaces[J].Waves in Random Media，1994,，4(3)：337-367.

此內容為AET網站原創(chuàng),，未經授權禁止轉載。