徐振武,,徐志京
(上海海事大學(xué) 信息工程學(xué)院,上海 201306)
摘要:經(jīng)典的Harris算法在提取圖像的角點上具有計算簡單,、適應(yīng)性強等優(yōu)勢,,但該方法由于人為設(shè)定單一閾值,容易出現(xiàn)偽角點,、漏檢點及運行速度不理想等現(xiàn)象,。針對這一情況,,文章在傳統(tǒng)Harris算法基礎(chǔ)上提出一種新的檢測方法,,采用多閾值的圓形非極大值抑制法提取角點, 以此降低算法檢測時間并增強圖像旋轉(zhuǎn)不變性,再借鑒SUSAN思想消去大部分偽角點,。通過實驗對比,,該算法具有更好的角點檢測性,為后期的圖像配準(zhǔn)奠定了良好的基礎(chǔ),。
關(guān)鍵詞: Harris角點檢測,;圓形區(qū)域;多閾值,;SUSAN算法
0引言
隨著近代計算機的迅速發(fā)展,,人們?yōu)榱双@取更高像素更寬視角的圖像以作科學(xué)研究,圖像拼接逐漸成為了計算機各領(lǐng)域的研究熱點[12],。
圖像蘊含有豐富的信息特征,,其中角點特征是圖像拼接領(lǐng)域的主要技術(shù)指標(biāo),業(yè)界對角點沒有統(tǒng)一定義,,一般被認為是圖像像素點亮度發(fā)生了劇烈改變或邊緣曲線曲率極大值的點[3],, 它能以極少的數(shù)據(jù)量來表現(xiàn)圖像的整體信息, 這有利于圖像處理的速度與精度,。角點檢測方法在圖像拼接中的配準(zhǔn),、融合、 定位等方面起著重要作用,, 其提取的好壞決定圖像拼接的質(zhì)量結(jié)果,。適量恰當(dāng)?shù)恼_角點在圖像拼接過程中可增強圖像的抗噪性和圖像形變的適應(yīng)能力,有利于圖像的后續(xù)匹配,使得實時處理成為可能,。
目前角點的檢測方法大致分兩種:基于圖像邊緣特征的角點檢測, 該算法依賴于圖像邊緣特征[4],,提取邊緣信息而求得角點,但算法定位精度差,,對噪聲敏感,;基于圖像灰度的角點檢測,,該方法依賴于像素點的曲率與梯度值信息。其中Harris算法[5]是一種被大眾所熟知的算法, 可較好地提取角點,。該算法雖然是一種優(yōu)秀的檢測方法, 但研究發(fā)現(xiàn)存在不足:
?。?)人為單一閾值的設(shè)定會對角點提取產(chǎn)生不確定的影響;
?。?)算法中所用的高斯平滑函數(shù)對圖像的誤檢及漏檢產(chǎn)生難以把控,;
(3)Harris算子的運行速度不夠理想,。
而對Harris的改進一直是圖像研究的熱點,,參考文獻[6]提出采用自適應(yīng)閾值的方法能達到更快更精確提取角點的效果,但在圖像的抗噪性和適應(yīng)圖像形變能力上略顯不足,;而參考文獻[7]提出的改進方法能滿足要求,,但在運算速度上又略顯欠缺。
針對上述不足,,本文提出基于Harris的改進方法,,采用多閾值的圓形區(qū)域非極大值抑制,再結(jié)合SUSAN思想達到檢測效果,。
1Harris角點檢測算法簡介
角點檢測的鼻祖是Moravec算法,,之后Harris在Moravec算子思想上提出Harris算法。
Harris算法的思想是定義一組矩形區(qū)域窗口中圖像灰度誤差的總和為任意方向上的自相關(guān)值[8],。圖1表示圖像邊緣在不同區(qū)域的變化情況,。圖1(a)、(b)窗口在邊緣上沒變化,,而(c)的窗口在各個方向上具有明顯的變化,,根據(jù)此現(xiàn)象,可將(c)作為角點,。
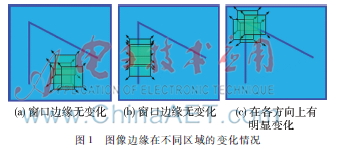
窗口平移[u,v]的量產(chǎn)生的圖像灰度變化E(u,v):
E(u,v)=∑x,yw(x,y)[I(x+u,y+v)-I(x,y)]2(1)
由I(x+u,,y+v)=I(x,y)+Ixu+Iyv+O(u2+v2)
得:

由于矩陣M=AC
CB特征值不易計算,通常計算式(5),,R為角點響應(yīng)值(CRF),,大小為:
R=detM-k(traceM)2(5)
其中,detM=λ1λ2=AC-B2,traceM=λ1λ2=A+C,detM是矩陣M的行列式;traceM是矩陣M的跡;k是經(jīng)驗常數(shù),,取0.04~0.06,。若R>CRFmax,則此像素點可提取為角點,。
為了避免在求CRF時設(shè)定k,,這里參考文獻[7]:
R=[I2x*I2y-(IxIy)2]/(I2x+I2y+ε)(6)
ε表示任意小的正數(shù)。
2改進的Harris角點檢測算法
2.1算法思想
本文采用多閾值方法。首先設(shè)定初始閾值并采用圓形區(qū)域非極大值抑制來提取大部分的候選角點,,之后對圖像作等比分塊處理,。利用塊的自適應(yīng)閾值求塊的補充角點。以此達到避免單一閾值下角點缺失或較多偽角點現(xiàn)象,。
傳統(tǒng)Harris算法常用3×3(大小可調(diào))為模板區(qū)域?qū)D像非極大值抑制:模板中心點與其余8點逐一比較大小,,若中心點響應(yīng)值大于其他任一模板內(nèi)響應(yīng)值,則該中心點被認為是角點,。同理圓形窗口下以圓心作為中心點,,若比較后中心點響應(yīng)值最大,則作為候選角點提取,,圓心位置順序遞增,,相反則舍棄該點,進行下一輪非極大值抑制,。
運用矩形模板區(qū)域非極大值抑制時,,如果圖像發(fā)生旋轉(zhuǎn)變化,窗口也發(fā)生變化,,因此增加了誤檢與漏檢的風(fēng)險,。而根據(jù)圓的旋轉(zhuǎn)不變性,采用圓形窗口能夠提高圖像旋轉(zhuǎn)不變性,。
2.2算法實現(xiàn)步驟
(1)初始角點RA提取
在初始閾值下,,利用圓形區(qū)域進行非極大值抑制方法求得候選角點集合A并計算A中每個像素點的CRF值R,,取最大Rmax0,令基礎(chǔ)閾值:
T0=c0×Rmax0(7)
c0為常數(shù),。當(dāng)c0取0.02~0.04 時可滿足要求,。
令R>T0且R為模板區(qū)域內(nèi)極大值的點A,記為初始角點RA,。
?。?)塊角點RB提取
將一個V×W圖像切割為M×N塊數(shù)量,塊的尺寸為(V/M)×(W/N)。在塊中求除了RA之外的Rmax值,。將第[p,q]塊的最大R記為Rmax B(p,q),,設(shè)置塊閾值為:
TB(p,q)=cB×Rmax B(p,q)(8)
cB為常數(shù),取值0.1~0.3時檢測出的塊角點RB能夠很好地彌補初始角點的欠缺,。
(3)SUSAN思想消除誤檢
SUSAN算法能消去誤檢點,,并具有較好的抗噪性,其步驟:初置閾值s并定義一圓形模板,,用此模板逐一比照圖像每一區(qū)域,。 若模板中心點(核)灰度值與模板內(nèi)某像素點灰度差小于s,即該點與中心點(核)具有相似灰度值,。所有類似的點組成的區(qū)域叫做USAN,,SUSAN算法示意圖如圖2所示,。
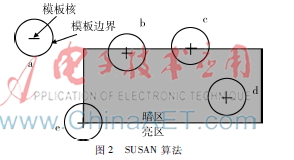
算法上, 用圓形模板掃描整幅圖像, 當(dāng)模板在灰色區(qū)域如圖2中的d, USAN面積最大,;當(dāng)模板接近灰色區(qū)域邊緣圖b時,,USAN面積慢慢減小,;當(dāng)核在灰色區(qū)域邊緣時如圖c,, USAN面積很小,;在核處于角上時如圖e,,USAN面積最小。
由此利用圓形模板掃描RA,、RB可刪除誤檢點,。設(shè)像素點(m,n)為RB的角點,若以(m,n)為核的USAN面積大于1/2模板面積即認為該點為誤檢點。如此便可略去大部分誤檢點,。
3實驗結(jié)果與分析
對于改進Harris角點檢測算法一直是圖像拼接等領(lǐng)域研究的熱點,,針對Harris算子的不足,各方法的改進都側(cè)有不同,,本文結(jié)合傳統(tǒng)Harris,、參考文獻[7]的改進算法做一個簡單比較。
實驗中,,先采用一張角點較明顯的圖,,對傳統(tǒng)Harris、參考文獻[7]及本文算法進行對比,。為了客觀比較,,與參考文獻[7]相同,本文傳統(tǒng)算法閾值大小也采用1 200,,比較結(jié)果如圖3所示,。

圖3(a)傳統(tǒng)Harris算法中,,提取出較多角點數(shù)量,,且在這張角點分明的圖像里,有著稍微的角點聚簇現(xiàn)象,,而誤檢點數(shù)較其他兩圖亦是最多,,且處理時間也比較長;而參考文獻[7]與本文算法所得到角點分布圖較為相近,,角點數(shù)較傳統(tǒng)算法有所減少,,分布也較均勻。但對比兩圖,統(tǒng)計圖中3種角點數(shù)量,,如表1所示,,不難看出本文算法更出色,其正確角點及漏檢角點雖然相似,,但誤檢數(shù)量更少,,有利于圖像拼接后續(xù)的配準(zhǔn)工作。

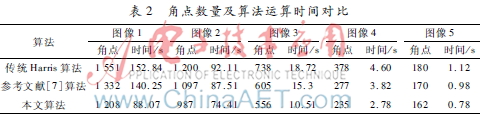
本文所用圓形區(qū)域非極大值抑制,,不但在運算時間上表2角點數(shù)量及算法運算時間對比算法圖像1圖像2圖像3圖像4圖像5角點時間/s角點時間/s角點時間/s角點時間/s角點時間/s傳統(tǒng)Harris算法1 551152.841 20092.1173818.723784.601801.12參考文獻[7]算法1 332140.251 09787.5160515.32773.821700.98本文算法1 20888.0798774.4155610.512352.781620.78有優(yōu)化,,而且對圖像旋轉(zhuǎn)不變性也有不錯的改善。圖4是對圖像作45°旋轉(zhuǎn)后算法對比:

圖4對圖像作45°旋轉(zhuǎn)后算法對比圖4(a)對比圖3(a),,經(jīng)45°旋轉(zhuǎn)后,,傳統(tǒng)Harris算法能提取出大部分的角點,但存在較嚴重的漏檢現(xiàn)象,。采用本文算法,,對比圖3(c)與圖4(c)的圖像旋轉(zhuǎn)角點檢測狀況可知,旋轉(zhuǎn)前后,,均能很好地檢測出角點,,漏檢與誤檢現(xiàn)象雖然存在,但比傳統(tǒng)算法好,。比較參考文獻[7]方法,,本文算法在采用圓形非極大值抑制后,具有更多的正確角點和更少的誤檢點,。
Harris算子本身具有不錯的抗噪性,,但本文在采用SUSAN思想后能增強算法的抗噪性。圖5是在0.1的高斯噪聲下效果對比,。
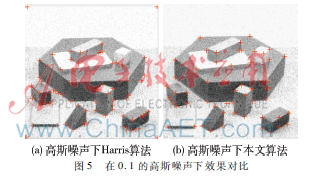
從圖5可以看出,本文算法在高斯噪聲環(huán)境下有不錯的表現(xiàn),,特別是偽角點檢測上,。經(jīng)過大量圖像角點處理實驗證明,本文算法在消除誤檢點效果上好于原算法,,因此認為具有更強的抗噪性,。
在圖像處理的時間上,對比本文算法較傳統(tǒng)算法也略有優(yōu)勢,。為客觀比較,,本文采用上海海事大學(xué)信息工程學(xué)院為背景的圖像,由Android手機拍攝,,原圖尺寸為:5 248×3 936,,利用圖像編輯軟件進行等比例縮放,其尺寸分別為:3 726×2 794、2 624×1 698,、1 312×984,、656×492、328×246,。
隨著圖像分辨率的降低,,角點數(shù)也在減少,這是可預(yù)見的,,因為高分辨率圖像勢必具有更豐富的細節(jié)信息,,所能提取的角點數(shù)目也更多。由表2可知,,相較于傳統(tǒng)Harris和參考文獻[7]算法,,本文介紹的算法能在涵蓋圖像的特征情況下提取出相對少的角點,且運行速度也可圈可點,,因此認為在算法性能上要好于另外2種,。圖6是表2的圖像4,尺寸大小為656×492,。

綜上圖示及表數(shù)據(jù),,本文算法在漏檢、誤檢都有不錯表現(xiàn),,利用該算法,,能夠很好地檢測出正確角點,同時能改善傳統(tǒng)算法在角點的聚簇現(xiàn)象,,勻化角點分布,,有利于后面的圖像配準(zhǔn)處理。
4結(jié)束語
在基于灰度的角點檢測算法中,,被大眾所知的經(jīng)典Harris算法具有不錯的效果,,能滿足日常應(yīng)用,并且對該方法的改進一直是一個熱點話題,。本文基于傳統(tǒng)Harris算法在圖像拼接領(lǐng)域應(yīng)用的不足,,提出改進思想,采用多閾值的圓形非極大值抑制法提取角點并利用SUSAN思想去除誤檢點,,經(jīng)實驗證明,,在運算時間及消除多余的誤檢點以及減少漏檢現(xiàn)象上有明顯的改善,具備比較好的角點檢測性能,,此方面的性能提升,,可為后期獲得更好圖像拼接效果提供一個算法參考。
參考文獻
?。?] TUYTELAARS T,,MIKOLAJCZYK K. Local invariant feature detectors: a survey[J].Foundations and Trendsin Computer Graphicsand Vision,,2008,3(3): 177280.
?。?] 仇國慶,,馮漢青,蔣天躍,,等.一種改進的Harris角點圖像拼接算法[J].計算機科學(xué),,2012,39(11):264266
[3] SMITH A M, BRADY J M. Susan: A new approach to low level image processing[J] . International Journal of Computer Vision, 1997, 23(1): 4578.
?。?] HARRIS C, SATEPHENS M J. A combined corner and edge detector[J]. Image Vision Computting, 1988, 6(1): 121128.
?。?] 涂春平,柴亞輝,,李廣麗,,等.一種基于Harris角點特征精確匹配的圖像拼接方法[J].實驗室研究與探索,2011,30(10):4043.
[6] 沈士喆,,張小龍,, 衡偉.一種自適應(yīng)閾值的預(yù)篩選Harris角點檢測方法[J].?dāng)?shù)據(jù)采集與處理,2011,,26(2):207213.
?。?] 毛雁明. 一種改進的基于Harris的角點檢測方法[D].昆明: 云南師范大學(xué),2009.
?。?] 龍伶敏. 基于Adaboost的人臉檢測方法及眼睛定位算法研究[D]. 成都: 電子科技大學(xué),,2008.

