王宏昊, 陳明, 張坤
(哈爾濱理工大學(xué) 測控技術(shù)與通信工程學(xué)院, 黑龍江 哈爾濱 150080)
摘要:設(shè)計了一款基于嵌入式處理器STM32的四旋翼飛行器,利用低成本傳感器測量加速度和機(jī)體的角速率,提出一種結(jié)合算法,從而實現(xiàn)飛行器姿態(tài)的精確測量。采用四元數(shù)法描述飛行器的姿態(tài),在測量過程中結(jié)合互補(bǔ)濾波算法進(jìn)行測量數(shù)據(jù)的矯正;同時針對出現(xiàn)的隨機(jī)噪聲干擾,采用卡爾曼濾波算法,實現(xiàn)姿態(tài)的準(zhǔn)確測量,最終在實際的飛行器平臺上得到了驗證。
關(guān)鍵詞:四旋翼;互補(bǔ)濾波;卡爾曼濾波;姿態(tài)控制
0引言
近年來,無人飛行器逐漸成為人們研究的熱點。無人飛行器的種類繁多,其中四旋翼無人飛行器是一個重要的研究方向[1]。與其他無人飛行器相比,四旋翼飛行器可以實現(xiàn)垂直起降、定點懸停,具有體積小、機(jī)動性能好等優(yōu)勢,尤其適用于災(zāi)害搜救、航空拍攝和特殊環(huán)境的巡視偵查等方面[2]。隨著無人飛行器在民用領(lǐng)域的發(fā)展,四旋翼飛行器更以其成本低廉的優(yōu)點得到了廣泛的應(yīng)用。
飛行器的位姿估計是實現(xiàn)UAV自主能力飛行的基礎(chǔ)。由于微機(jī)電系統(tǒng)(Micro Electro Mechanical System,MEMS)具有成本低廉、體積小、功耗低的優(yōu)點,MEMS被廣泛應(yīng)用于無人機(jī)的慣性導(dǎo)航領(lǐng)域。然而,低成本的傳感器具有嚴(yán)重的時變漂移,因此需要采用有效的算法實時估計傳感器的漂移,抑制姿態(tài)誤差的累計。至今,國內(nèi)外已經(jīng)有很多學(xué)者在這方面做了很多工作,參考文獻(xiàn)[3]使用卡爾曼濾波算法對加速度傳感器數(shù)據(jù)和陀螺儀數(shù)據(jù)進(jìn)行融合,實時地改變測量噪聲協(xié)方差的值,避免了動態(tài)噪聲對加速度傳感器的影響,提高了飛行器姿態(tài)測量的精度;參考文獻(xiàn)[4]提出了基于四元數(shù)的姿態(tài)估計方法,并采用了低功耗的傳感器。本文設(shè)計了一款低成本的四旋翼飛行器,結(jié)合四元數(shù)與互補(bǔ)濾波與卡爾曼濾波算法,實現(xiàn)了對飛行器位姿的有效與精確估計,并在實際中得到了驗證。
1硬件設(shè)計
為了設(shè)計體積小、重量輕、功耗低的姿態(tài)航向參考系統(tǒng),本文選擇集成度高的嵌入式處理器STM32F103作為導(dǎo)航核心處理器,實現(xiàn)姿態(tài)和航向解算以及輸出。使用集成加速度計和陀螺儀的MPU6050測量加速度和機(jī)體的角速率。加速度計比較敏感、變化速度快,在低動態(tài)下可以解算得到比較準(zhǔn)確的姿態(tài)角;而在高速狀態(tài)下,加速度計在飛行過程中釆集到的數(shù)據(jù)帶有大量的噪聲(主要是由震動產(chǎn)生的),解算傳來的姿態(tài)角也就有了較大的誤差。在加速度較大的情況下,加速度計解算的姿態(tài)角變得不可靠,需要使用陀螺儀測量的角速率積分來修正姿態(tài)陀螺儀傳感器輸出變化緩慢,但是時間長了有較大的累積誤差,而且還有溫度漂移。利用陀螺儀進(jìn)行物體姿態(tài)檢測需要考慮到累計誤差的消除[5]。因此在四軸飛行器的飛行姿態(tài)控制系統(tǒng)中,必須將陀螺儀和加速度計的數(shù)據(jù)通過數(shù)據(jù)濾波算法進(jìn)行融合和濾除噪聲干擾,以此來得到正確的姿態(tài)數(shù)據(jù)。
2飛行器姿態(tài)估計算法
2.1四元數(shù)法
四旋翼無人飛行器姿態(tài)解算是將飛行器上慣性單元的輸出實時轉(zhuǎn)換成飛行器的姿態(tài),即飛行器的機(jī)體坐標(biāo)系(xB,yB,zB)相對于導(dǎo)航坐標(biāo)系(XE,YE,ZE)的角位置。

歐拉角是飛行器的3個姿態(tài)角,即俯仰角(pitch)、橫滾角(roll)、偏航角(yaw)。根據(jù)歐拉旋轉(zhuǎn)定律,可用3次旋轉(zhuǎn)使得機(jī)體坐標(biāo)系與導(dǎo)航坐標(biāo)系重合,每一次旋轉(zhuǎn)都是以導(dǎo)航標(biāo)系的x、y、z軸中的一個坐標(biāo)軸來轉(zhuǎn)動,轉(zhuǎn)過的角就是歐拉角,每次旋轉(zhuǎn)后坐標(biāo)關(guān)系可由一旋轉(zhuǎn)矩陣來表示,即方向余弦矩陣:
![~5]ITAKI5B6SP8AO_EC5HB0.png ~5]ITAKI5B6SP8AO_EC5HB0.png](http://files.chinaaet.com/images/2016/08/23/6360757433899700009369471.png)
式中φ、、θ分別代表偏航角、橫滾角、俯仰角。為避免歐拉角在表示姿態(tài)時可能出現(xiàn)的奇異問題,四元數(shù)在飛行器的姿態(tài)表示方面得到了廣泛的應(yīng)用。設(shè)描述四旋翼飛行器姿態(tài)的四元數(shù)為:
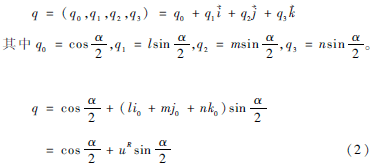
導(dǎo)航坐標(biāo)系與機(jī)體坐標(biāo)系之間的坐標(biāo)關(guān)系可用方向余弦矩陣表示,其四元數(shù)形式為:

導(dǎo)航坐標(biāo)系到機(jī)體坐標(biāo)系的旋轉(zhuǎn)過程中坐標(biāo)系始終保持直角坐標(biāo)系,所以CBE為正交矩陣,即CBE=(CBE)-1=(CBE)T。可得飛行器的姿態(tài)角為:

將四元數(shù)代入可得到:
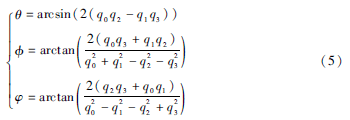
四元數(shù)的微分方程為=12Ωbnbq,即:
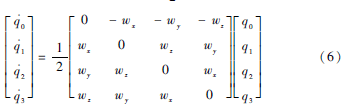
式中wx、wy、wz為機(jī)體坐標(biāo)系下的角速度。在已知初始四元數(shù)的情況下,通過三軸陀螺儀測量的3個軸的角速度就可以實時更新四元數(shù)的值,進(jìn)而更新姿態(tài)角獲得姿態(tài)信息[6]。
2.2互補(bǔ)濾波補(bǔ)償算法
陀螺儀存在積分誤差,所以解算出來的姿態(tài)角也會出現(xiàn)偏差。為了解決這一問題,引入互補(bǔ)濾波算法,利用加速度計來修正陀螺儀的誤差[7]。設(shè)加速度計測出來的重力向量為ax、ay、az,陀螺儀積分后的姿態(tài)推算出來的重力向量為vx、vy、vz,則有:
vx=2(q1q3+q2q4)
vy=2(q2q3-q0q1)
vz=(q20-q21-q22+q23)(7)
從而陀螺儀積分后的姿態(tài)結(jié)合加速度計數(shù)據(jù)得到的姿態(tài)誤差為:
ex=(ayvz-azvy)
ey=(azvx-axvz)
ez=(axvy-azvx)(8)
此姿態(tài)誤差與陀螺儀積分誤差成正比,使用互補(bǔ)濾波算法來修正陀螺儀角速度積分誤差:
xint=exint+ex*ki
yint=eyint+ey*ki
zint=ezint+ez*ki (9)
其中xint、yint、zint是對陀螺儀的糾正量的積分項,ki為積分系數(shù)。
x=ωx+kpex+exint
y=ωy+kpey+eyint
z=ωz+kpez+ezint (10)
其中x、y、z為陀螺儀修正后的輸出角速度,kp為比例系數(shù)。
2.3基于姿態(tài)角的卡爾曼濾波算法
在實際測試中,上位機(jī)接收到姿態(tài)角的數(shù)據(jù)仍然存在少許的噪聲干擾,為了濾除噪聲的干擾,引入卡爾曼濾波算法[8]。設(shè)姿態(tài)角為α,對其離散化并構(gòu)造狀態(tài)方程和觀測方程:
αk=Aαk-1+Wk-1
Zk=Hkαk+Vk(11)
算法步驟如下。
(1)狀態(tài)一步預(yù)測。通過第k-1時刻的α值,預(yù)測第k時刻的α值:
αk|k-1=αk
(2)一步預(yù)測均方誤差。根據(jù)第k-1時刻的系統(tǒng)誤差估計第k時刻的系統(tǒng)預(yù)測誤差Pk k-1 :
Pk|k-1=Pk-1+Q
(3)濾波增益計算:
Kk=Pk|k-1/(Pk|k-1+R)
(4)狀態(tài)更新,計算系統(tǒng)最優(yōu)估算值:
αk=αk-1+K(Zk-αk-1)
(5)濾波均方誤差更新。在卡爾曼濾波運(yùn)算中,要實現(xiàn)對均方誤差的更新,以便下一刻計算卡爾曼增益,更新方程如下:
Pk=(1-Kk)Pk|k-1
3軟件設(shè)計思路
在STM32和MPU6050等傳感器上電后,程序首先進(jìn)行系統(tǒng)的初始化,在初始化中配置MCU以及傳感器,設(shè)定卡爾曼濾波器參數(shù),然后獲取傳感器數(shù)據(jù),傳感器的數(shù)據(jù)經(jīng)過換算得到陀螺儀和加速度計的測量值。利用加速度的測量值修正陀螺儀的輸出,再通過修正后的角速度更新四元數(shù),進(jìn)而解算得到姿態(tài)角。由于仍然有噪聲的干擾,因此采用卡爾曼濾波算法對姿態(tài)角進(jìn)行濾波,從而得到正確的姿態(tài)角[9]。具體軟件流程如圖1所示。

4實驗結(jié)果與分析
在現(xiàn)有的四旋翼飛行器平臺上,運(yùn)用上述算法進(jìn)行實驗。初始時刻,將四旋翼置于水平,然后改變四旋翼的航向,獲取俯仰角、滾轉(zhuǎn)角、偏航角的數(shù)據(jù),通過藍(lán)牙傳送到上位機(jī),得到3個姿態(tài)角的輸出,如圖2~圖4所示。

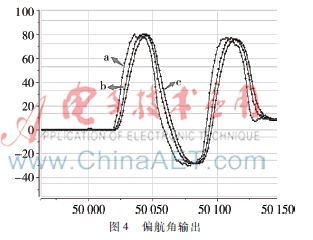
其中,a、b、c分別表示加速度計解算出來的姿態(tài)角輸出、四元數(shù)法解算出來的姿態(tài)角輸出和卡爾曼濾波后的姿態(tài)角輸出。
5結(jié)論
本文設(shè)計了由低成本傳感器組成的四旋翼飛行器,針對傳感器測量數(shù)據(jù)誤差的復(fù)雜性與累積性,通過使用四元數(shù)法描述姿態(tài),避免了用歐拉角描述姿態(tài)的奇異值問題,同時引入互補(bǔ)濾波與卡爾曼濾波算法,從而更加精確地獲得飛行器的實時精確姿態(tài)信息,并在實際的觀測中得到了驗證,結(jié)果十分理想,為有效地控制飛行器平臺姿態(tài)并最終實現(xiàn)無人飛行打下了良好的基礎(chǔ)。
參考文獻(xiàn)
[1] KUMAR V, MICHAEL N. Opportunities and challenges with autonomous micro aerial vehicles[J]. The International Journal of Robotics Research, 2012, 31(11) : 12791291.
[2] BOUABDALLAH S. Design and control of quadrotors with application to autonomous flyin[D]. Lausanne: Ecole Polytechnique Federale De Lausanne, 2007.
[3] Wang Shaohua, Yang Ying. Quadrotor aircraft attitude estimation and control based on Kalman filter[C]. Proceedings of the 31st Chinese Control Conference, 2012,30(9):56345639.
[4] Chao Haiyang, COMMPMANS C, Di Long, et al. A comparative evaluation of lowcost IMUs for unmanned autonomous systems[C]. IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, 2010:211216.
[5] LAM Q M, STAMATAKOS N, WOODRUFF C, et al. Gyro modeling and estimation of its random noise sources[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, Texas, 2003.
[6] KRAJNIK T, VONASEK V, FISER D, et al. Ardrone as a platform for robotic research and education[A]. OBDRZALEK D, GOTTSCHEBER A. Communications in Computer and Information Science[C]. Springer, 2011, 161: 172186.
[7] BRISTEAU P J, CALLOU F, VISSIERE D, et al. The navigation and control technology inside the ar.drone micro uav[C]. Proceedings of the 18th IFAC World Congress, Milan, Italy, AugustSeptember 2011, 2011,18:14771484.
[8] Wu Xingming, Duan Li, Chen Weihai. A Kalman filter approach based on random drift data of fiber optic gyro[C]. 2011 6th IEEE Conference on Industrial Electronics and Applications (ICIEA), 2011:19331937.
[9] 劉曉杰,趙曉輝,顧海軍. 微小型四旋翼無人機(jī)實時嵌入式控制系統(tǒng)設(shè)計與實現(xiàn)[J].電子技術(shù)應(yīng)用,2009,35(5):3637.
[10] 楊萌,雷建和,胡廷軒,等. 基于STM32的四旋翼飛行器控制系統(tǒng)設(shè)計[J].微型機(jī)與應(yīng)用,2015,34(12):7679.

