顧天1,，李曉麗1，趙曙光1,，鄭鵬遠(yuǎn)2

　?。?.東華大學(xué) 信息科學(xué)與技術(shù)學(xué)院，上海 201620,； 2.上海電力學(xué)院 自動(dòng)化工程學(xué)院,，上海 200090）

      摘要：網(wǎng)絡(luò)系統(tǒng)的規(guī)模不斷擴(kuò)展，趨向于龐大復(fù)雜化,。文章針對(duì)系統(tǒng)內(nèi)部信息傳遞所帶來(lái)的控制滯后等問(wèn)題,，在網(wǎng)絡(luò)系統(tǒng)能控的研究基礎(chǔ)上引入能控性指數(shù)的概念，用以描述網(wǎng)絡(luò)系統(tǒng)能控的性能指標(biāo),；基于二分圖提出算法獲得網(wǎng)絡(luò)系統(tǒng)能控性指數(shù),，并提供每個(gè)控制量相應(yīng)的控制鏈，為后續(xù)劃分大規(guī)模網(wǎng)絡(luò)系統(tǒng)的節(jié)點(diǎn)群等研究工作提供科學(xué)依據(jù),。

　　關(guān)鍵詞：網(wǎng)絡(luò)系統(tǒng),；二分圖；能控性指數(shù)

0引言

　　隨著計(jì)算機(jī)技術(shù)的飛速發(fā)展,，出現(xiàn)了越來(lái)越多規(guī)模龐大且結(jié)構(gòu)復(fù)雜的網(wǎng)絡(luò),，其通常具有空間分布式特征，例如跨區(qū)域的電力網(wǎng),、縱橫交錯(cuò)的交通網(wǎng)等,。對(duì)網(wǎng)絡(luò)中若干節(jié)點(diǎn)施加控制以實(shí)現(xiàn)整個(gè)網(wǎng)絡(luò)能控，對(duì)網(wǎng)絡(luò)系統(tǒng)的可控性進(jìn)行分析,，可望在進(jìn)入定量研究前先得到全局的指導(dǎo)信息［1］ ，有助于理解各控制量對(duì)網(wǎng)絡(luò)系統(tǒng)的影響,。目前網(wǎng)絡(luò)系統(tǒng)的可控性是指在不限制控制步數(shù)的情況下,，通過(guò)施加控制量使其可控，但隨著網(wǎng)絡(luò)規(guī)模的不斷擴(kuò)大,，網(wǎng)絡(luò)系統(tǒng)的各個(gè)組成部分彼此間傳遞信息或狀態(tài)會(huì)帶來(lái)控制作用滯后等問(wèn)題［2］,。通過(guò)基于能控性指數(shù)的算法研究可以將大網(wǎng)絡(luò)系統(tǒng)分散化進(jìn)行控制，縮短了控制過(guò)程,。

1問(wèn)題描述及判據(jù)

　　大規(guī)模網(wǎng)絡(luò)系統(tǒng)具有極其復(fù)雜的結(jié)構(gòu)和不穩(wěn)定性,。針對(duì)高維性、非線性的大系統(tǒng),，研究其可控性問(wèn)題十分復(fù)雜,，可以將其轉(zhuǎn)化為在一定范圍內(nèi)按不同工作點(diǎn)線性化所得的線性系統(tǒng)，進(jìn)而分析轉(zhuǎn)化后的線性系統(tǒng)是否可控［1］ ,?？紤]由n個(gè)節(jié)點(diǎn)構(gòu)成的線性時(shí)不變網(wǎng)絡(luò)系統(tǒng):

　　(t)=Ax(t)+Bu(t)(x∈Rn,u∈Rm)(1)

　　令G(α,β)為一個(gè)有向圖用以描述網(wǎng)絡(luò),，節(jié)點(diǎn)集α={1,2...n}，邊集β=α×α,，一條邊(i,j)∈β表示節(jié)點(diǎn)i可達(dá)節(jié)點(diǎn)j,，但反之不成立。由i向j所建立的聯(lián)系表示為aij,，無(wú)法建立聯(lián)系則為0,。j為i的鄰接節(jié)點(diǎn)，定義Ni為i的所有鄰接節(jié)點(diǎn)的集合,，j∈Ni,。n×n維常值矩陣A用以描述網(wǎng)絡(luò)各節(jié)點(diǎn)間的關(guān)聯(lián)情況；B為n×m維常值輸入矩陣,，表示控制器對(duì)節(jié)點(diǎn)的影響［3］,，若對(duì)節(jié)點(diǎn)j直接施加控制器uj則表示為bj。

　　定義1:系統(tǒng)(1)可控的充要條件：

　　rank［B,AB,A2B...An－1B］=n(2)

　　網(wǎng)絡(luò)系統(tǒng)可控表明其可由任意初始狀態(tài)受控制器驅(qū)動(dòng)到達(dá)任何所需的最終狀態(tài)［4］,。其中矩陣An－1B本質(zhì)上體現(xiàn)了從控制器出發(fā)在n－1步路徑內(nèi)與網(wǎng)絡(luò)系統(tǒng)所有節(jié)點(diǎn)建立了聯(lián)系,，根據(jù)定義1引入網(wǎng)絡(luò)能控性指數(shù)μ，對(duì)于n維連續(xù)時(shí)間線性時(shí)不變系統(tǒng),，能控性指數(shù)μ定義如下：

　　定義2:系統(tǒng)(1)k步可控的充要條件：

　　gr［B,AB,A2B...AkB］=n(3)

　　滿足式(3)的k的最小值即為能控性指數(shù)μ,。

　　圖1為由4個(gè)節(jié)點(diǎn)構(gòu)成的網(wǎng)絡(luò)系統(tǒng)，對(duì)其進(jìn)行分析,。

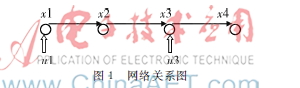
　　其中常值矩陣A,、B為：

　　分析發(fā)現(xiàn)gr［B,AB,A2B,A3B］=4，符合定義1與定義2,，表明該網(wǎng)絡(luò)系統(tǒng)可控,，也可稱之為3步可控。同時(shí)gr［B,AB］=4,，符合定義2,，而gr［B］<4,則滿足條件的k的最小值為1，即能控性指數(shù)為1,，控制鏈如圖2所示,。

2算法

　　將一個(gè)圖的頂點(diǎn)劃分為兩個(gè)不相交集U和V，使得連邊分別連接U,、V中的頂點(diǎn),，若存在這樣的劃分則此圖就是一個(gè)二分圖，而邊數(shù)最多的匹配方法即為最大匹配［5］,。通過(guò)最大匹配能解決很多實(shí)際問(wèn)題,，如棋盤走法、配對(duì)問(wèn)題等,。匈牙利數(shù)學(xué)家Edmonds對(duì)二分圖的最大匹配進(jìn)行研究并得到一種普適性的匈牙利算法,。

　　2.1匈牙利算法

　　以圖3為例介紹匈牙利算法的基本思想,。

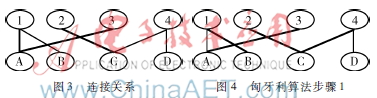
　　首先從1開始匹配：1-A，2-C,，3-A,，如圖3加粗路線，此時(shí)由于A已匹配給1,，因此將1-A轉(zhuǎn)變?yōu)?-B,，從而成功匹配3-A，如圖4所示,。

　　1繼續(xù)匹配4,，4-C，如圖4所示,。此時(shí)由于C已經(jīng)匹配給2,，為了形成更多的匹配邊，因此將4-C轉(zhuǎn)變?yōu)?-D,。最終圖5匈牙利算法步驟2最大匹配方案為1-B,、2-C、3-A,、4-D,，如圖5所示。

　　2.2算法Aci

　　研究網(wǎng)絡(luò)系統(tǒng)可控性時(shí),，可以將網(wǎng)絡(luò)表示為二分圖,，利用最大匹配理論匹配盡可能多的邊，得出為使網(wǎng)絡(luò)可控的一種控制器選取方案,，而本文基于可控網(wǎng)絡(luò)分析匹配方案以獲取能控性指數(shù),。

　　假設(shè)網(wǎng)絡(luò)系統(tǒng)如圖6所示。

　　通過(guò)匈牙利算法可知對(duì)節(jié)點(diǎn)1,、3,、5、9施加控制可使該網(wǎng)絡(luò)可控,，但分析控制方案時(shí)會(huì)出現(xiàn)圖7所示匹配方式：

　　由控制器u5控制的節(jié)點(diǎn)群5-6-7-2-8形成了一條控制鏈，但相比于1,、3-4,、9-10，該條控制鏈顯得較長(zhǎng),，易影響控制作用,。

　　在已知網(wǎng)絡(luò)可控的基礎(chǔ)上，從各控制量出發(fā),，根據(jù)節(jié)點(diǎn)間的可達(dá)關(guān)系逐步匹配節(jié)點(diǎn)形成或長(zhǎng)或短的控制鏈,。將一條控制鏈看作一個(gè)子系統(tǒng),，當(dāng)整個(gè)系統(tǒng)劃分成若干子系統(tǒng)后，若其分別為k1,k2,，…kn步可控,，定義其中最大值為kmax，則整個(gè)大系統(tǒng)稱為kmax步可控,。kmax需盡可能小,，當(dāng)其取值最小時(shí)即為能控性指數(shù)μ。

　　以控制器直接控制的節(jié)點(diǎn)i為起始點(diǎn),，同時(shí)進(jìn)行匹配,。由網(wǎng)絡(luò)可控可知每個(gè)節(jié)點(diǎn)都必存在于匹配邊中，因此若匹配完成后仍有節(jié)點(diǎn)未被匹配,，則必須改變某節(jié)點(diǎn)的匹配方式,，直至所有節(jié)點(diǎn)均被匹配。

　　能控性指數(shù)算法Aci描述如下：

　?。?）列出所有根節(jié)點(diǎn)i(1≤i≤n),；

　　（2）λ:根節(jié)點(diǎn)i的數(shù)目,設(shè)置k=0,；

　?。?）重復(fù)步驟（4）~（6）；

　?。?）匹配i的可達(dá)節(jié)點(diǎn)j(i－j),j∈Ni,若j出現(xiàn)重復(fù)則改變前者匹配方式,，j的數(shù)目為η,k=k+1,λ=λ+η；

　?。?）令j為新的根節(jié)點(diǎn),匹配其可達(dá)節(jié)點(diǎn),；

　　（6）當(dāng)η=0,λ≠n,節(jié)點(diǎn)σ未匹配(δ可達(dá)σ),退回δ所在步驟,改變其匹配方式為δ－σ,從該步驟開始繼續(xù)向下匹配,；

　?。?）直至λ=n，n為網(wǎng)絡(luò)節(jié)點(diǎn)數(shù)目,；

　?。?）所有節(jié)點(diǎn)已存在于匹配邊中,μ=k。

3仿真與結(jié)論

　　利用二分圖描述圖6所示網(wǎng)絡(luò),，如圖8所示,，箭頭表示始端節(jié)點(diǎn)可達(dá)末端節(jié)點(diǎn)，例如1指向2表示節(jié)點(diǎn)1可達(dá)節(jié)點(diǎn)2,。

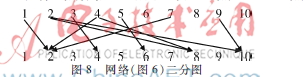
　　分析圖6網(wǎng)絡(luò),，n=10，k=0,，起始點(diǎn)為1,、3,、5、9,，λ=4,，第一步如圖9所示。

　　匹配節(jié)點(diǎn)為2,、4,、6、10,，η=4,。此時(shí)λ=8，k=1,，第二步如圖10所示,。

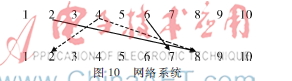
　　匹配節(jié)點(diǎn)為8、7,。其中4-2,，2在第一步就已匹配(舍去)，轉(zhuǎn)變?yōu)?-8,，而此步驟已將8分配給了2,，改變匹配方式2-10，而10在第一步就已匹配(舍去),，因此2向下不可再匹配,，η=2。此時(shí)λ=10=n,，所有節(jié)點(diǎn)已存在于匹配邊中,，k=2，μ=2,。

　　最終匹配方式如圖11所示,，控制鏈為：1-2；3-4-8,；5-6-7,；9-10。同時(shí)可驗(yàn)證gr［B,AB,A2B］=10,，k的最小值為2,，即能控性指數(shù)μ=2。

　　以圖12網(wǎng)絡(luò)系統(tǒng)為例,，可控性指數(shù)μ=5，通過(guò)匹配邊將原本關(guān)聯(lián)復(fù)雜的網(wǎng)絡(luò)分散化,，獲得各條結(jié)構(gòu)簡(jiǎn)單明了的控制鏈,，使得控制作用更有效,。

4結(jié)束語(yǔ)

　　本文引入網(wǎng)絡(luò)系統(tǒng)能控性指數(shù)的概念并給出能控性判據(jù)，在此基礎(chǔ)上提出算法Aci獲得能控性指數(shù)及相應(yīng)的控制鏈,，縮短了控制過(guò)程和時(shí)間,。在實(shí)際網(wǎng)絡(luò)如電網(wǎng)中，大量節(jié)點(diǎn)具有固定的匹配方式,，這樣就能為分析網(wǎng)絡(luò)的k步可控性節(jié)省大量時(shí)間,，同時(shí)研究各個(gè)控制器所控制的節(jié)點(diǎn)群，可以明顯地從復(fù)雜的網(wǎng)絡(luò)中得到各條清晰的控制鏈,，以各控制器為起始點(diǎn),，只需抓住這個(gè)起始點(diǎn)將其從網(wǎng)絡(luò)中抽出便可獲知該控制器依次控制的各個(gè)節(jié)點(diǎn)。對(duì)于研究某些實(shí)際網(wǎng)絡(luò)模型有很大的參考價(jià)值,，并可反過(guò)來(lái)服務(wù)于研究控制器的選取,。

　　參考文獻(xiàn)

　　［1］ 席裕庚.動(dòng)態(tài)大系統(tǒng)方法導(dǎo)論［M］.北京：國(guó)防工業(yè)出版社,1988.

　?。?］ 李健勇,羅永平,黃道穎,等.網(wǎng)絡(luò)控制系統(tǒng)時(shí)延分布分析與建模［J］.鄭州輕工業(yè)學(xué)院學(xué)報(bào)(自然科學(xué)版),2014,29(4):5053.

　?。?］ Liu Yangyu, SLOTINE J J, BARABA′SI A L. Controllability of complex networks［J］. Nature， 2011,，473（12）：167173.

　?。?］ 鄭大鐘.線性系統(tǒng)理論［M］.北京：清華大學(xué)出社,2011.

　　［5］ 邵長(zhǎng)城,張錫哲.復(fù)雜網(wǎng)絡(luò)可控性分析與驅(qū)動(dòng)節(jié)點(diǎn)集拓?fù)湫再|(zhì)研究［D］.沈陽(yáng)：東北大學(xué),2012.