0 引言

    建筑物內(nèi)部的結(jié)構(gòu)變化會引起工程安全上的事故,，通過采集和分析建筑物結(jié)構(gòu)的動力學(xué)特征參數(shù)，可以有效地判斷建筑結(jié)構(gòu)的安全情況,。振弦式傳感器可以將感受到的應(yīng)力轉(zhuǎn)化為頻率信號輸出,，具有結(jié)構(gòu)簡單、精度高,、穩(wěn)定性好的特點(diǎn),，已被廣泛應(yīng)用于“建筑結(jié)構(gòu)安全檢測”工程中^[1]。

    目前,，基于振弦式傳感器測頻系統(tǒng)的頻率測量方案分為時域法和頻域法兩大類^[2-3],。基于快速傅里葉變換(Fast Fourier Transformation,，F(xiàn)FT)的頻域法具有數(shù)據(jù)處理靈活,、測頻精度高、系統(tǒng)穩(wěn)定等優(yōu)點(diǎn),，并得到越來越廣泛的應(yīng)用,。FFT 變換存在兩個缺陷：(1)信號時域上的截斷會引起頻譜泄漏,，影響頻率估計的精度；(2)信號頻率不是FFT頻率分辨率的整數(shù)倍時存在柵欄效應(yīng),，會導(dǎo)致頻率估計產(chǎn)生較大的誤差,。學(xué)者們提出了多種頻率校正算法用于提高頻率估計的精度^[4-5]。其中,，全相位FFT算法具有抑制頻譜泄露的能力,，在頻率估計精度和抗噪聲上的性能優(yōu)異^[6]，可應(yīng)用于振弦式傳感器測頻系統(tǒng)中,。

    本文介紹了全相位FFT的實(shí)現(xiàn)方法,，并采用全相位FFT和Rife頻率校正算法，設(shè)計了一款基于STM32平臺的振弦式傳感器測頻系統(tǒng),。

1 系統(tǒng)組成

1.1 系統(tǒng)結(jié)構(gòu)框圖

    系統(tǒng)的結(jié)構(gòu)框圖如圖1所示,，主要包含STM32處理器模塊,、振弦式傳感器及其激振電路,、信號放大電路、濾波電路,、存儲器模塊等,。

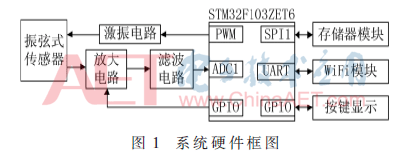
    振弦式傳感器在激振電路的作用下輸出一個微弱信號，經(jīng)過放大電路,、濾波電路后由STM32處理器內(nèi)部ADC進(jìn)行采樣,。采集的數(shù)據(jù)由軟件處理后，可以通過WiFi模塊上傳到上位機(jī),。

1.2 放大電路設(shè)計

    振弦式傳感器的輸出信號微弱,，一般為毫伏級別，需要經(jīng)過高增益放大電路才能進(jìn)行后續(xù)處理,。具體電路如圖2所示,。

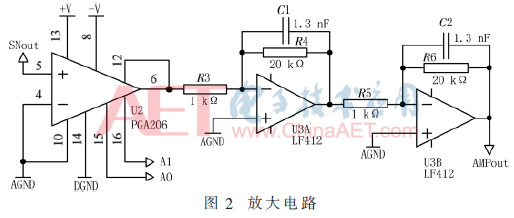
    由于傳感器安放位置的需要，信號采集電路到測頻系統(tǒng)之間的連接導(dǎo)線長度會有不同,。傳感器輸出的微弱信號在幾米長和幾百米長的導(dǎo)線中傳輸時,，信號衰減程度不一樣。為了保證傳感器信號滿足ADC采樣的要求,，系統(tǒng)采用儀表放大器PGA206設(shè)計了可編程增益放大電路,。

    前級放大器PGA206通過A0、A1選擇不同的放大倍數(shù)：1,、2,、4、8,；后兩級LF412運(yùn)算放大器構(gòu)成增益為400的放大器,。因此，整個系統(tǒng)可以選擇4種放大倍數(shù)：400、800,、1 600和3 200,。

1.3 濾波電路設(shè)計

    傳感器信號不可避免地存在噪聲和干擾，為了提高測量精度,，必須要對其進(jìn)行濾波,。傳感器輸出信號的頻率在400 Hz～5 000 Hz 之間，可以采用四階低通濾波器和四階高通濾波器構(gòu)成帶通濾波器,。系統(tǒng)設(shè)計的低通濾波器截止頻率為6 000 Hz,，高通濾波器截止頻率為400 Hz，具體電路如圖3所示,。

2 系統(tǒng)軟件設(shè)計

2.1 全相位FFT的實(shí)現(xiàn)

    全相位FFT綜合考慮和分析了包含信號樣本中心點(diǎn)的全部截斷組合,，具有良好的抑制頻譜泄露的性能。對于振弦式傳感器測頻系統(tǒng),，頻率為f₀的信號s(t)以采樣率f_s采樣2N-1個點(diǎn),，得到離散信號：

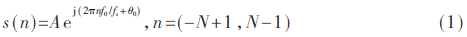
    利用全相位FFT測量頻率的步驟如下：

    (1)構(gòu)建兩個N點(diǎn)漢寧窗序列a(n)和b(n)。

    (2)將兩個窗序列求卷積,，得到卷積窗c(n),。

    (3)將2N-1個點(diǎn)的卷積窗c(n)進(jìn)行歸一化。

    (4)將2N-1個采樣點(diǎn)序列與卷積窗c(n)相乘,，得到加窗序列,。

    (5)將序列的每個(-N+i)項和i項折疊相加，得到新的N點(diǎn)序列d(n)：{x(0),，x(1)+x(-N+1),，x(2)+x(-N+2)，…,，x(-1)+x(N-1)},。

    (6)對d(n)進(jìn)行FFT變換得到全相位FFT頻譜。

    (7)利用Rife雙譜線校正算法估計頻率,。

    全相位FFT得到的是離散譜,，進(jìn)行頻率估計時需要進(jìn)行校正。Rife雙譜線校正算法具有公式簡單,、運(yùn)算快捷的優(yōu)點(diǎn),，易于在微處理器上實(shí)現(xiàn)。

    Rife雙譜線校正算法針對傳統(tǒng)FFT進(jìn)行頻率校正時,，頻率校正公式如式(2)所示^[7]：

式中,，k₀為FFT變換后最大譜線離散頻率索引值，|X(k₀)|為最大譜線的幅度,，|X(k₀+r)|為k0相鄰的次大譜線幅度,。r取值為±1,，根據(jù)次大譜線在最大譜線的位置決定。

2.2 系統(tǒng)軟件流程

    全相位FFT頻率估計是整個系統(tǒng)程序的核心,。為減少微處理器的運(yùn)算量,，對全相位FFT的處理步驟作了優(yōu)化處理。全相位FFT測頻步驟中的前3步可以先在MATLAB中實(shí)現(xiàn),，形成一個2N-1個元素的數(shù)組cn(即歸一化后的卷積窗c(n)),。相應(yīng)程序如下：

    N=1024； 采樣點(diǎn)數(shù)

    an=hanning(N)′,； 構(gòu)建漢寧窗

    bn=hanning(N)′,；

    cn=conv(an,bn)； 得到2N-1點(diǎn)卷積窗

    cn=cn/sum(cn),； 歸一化卷積窗

    將cn構(gòu)成的數(shù)組存入微處理器中,，再進(jìn)行往下的步驟，可以減少大量浮點(diǎn)數(shù)的運(yùn)算,。具體流程圖如圖4所示,。

    系統(tǒng)采用低壓反饋式復(fù)激振方法對傳感器進(jìn)行激勵^[9]，首先對傳感器用低壓單脈沖進(jìn)行預(yù)激振,。此時,，傳感器輸出的頻率信號幅度小,、衰減快,，使用傳統(tǒng)FFT對其測頻得到頻率f₀，測頻的相對誤差較大,。接下來對傳感器以f₀的頻率,、持續(xù)時間為100 ms的PWM波進(jìn)行復(fù)激振，再延時100 ms等待輸出的波形數(shù)據(jù)比較穩(wěn)定時采樣,。復(fù)激振時,，鋼弦達(dá)到共振的狀態(tài)，傳感器輸出的頻率信號幅度大,、衰減慢,，使用apFFT對其再次測頻，即可得到十分精確的信號頻率,，實(shí)現(xiàn)精確測頻,。具體流程如圖5所示。

3 系統(tǒng)測試

3.1 系統(tǒng)工作波形測試

    實(shí)驗室環(huán)境下,，將振弦傳感器接入系統(tǒng)并靠近220 V市電供電線纜,，人為引入外部干擾噪聲。示波器雙蹤觀察放大電路輸出的AMPout波形和經(jīng)過濾波電路后輸出的toADC波形如圖6所示,。

    從圖6可以看出,，傳感器受到市電50 Hz信號與其他外部噪聲的干擾,，經(jīng)過放大后的噪聲信號峰峰值高達(dá)2.4 V。噪聲信號經(jīng)過濾波電路后,，噪聲信號峰峰值僅剩180 mV,。濾波器對于帶外噪聲的濾波效果較好。

    圖7為一次測頻過程完整的波形,。通道1為傳感器輸出的頻率信號經(jīng)過放大濾波后的波形,，通道2為微處理器控制端輸出的波形。

    對比通道1和通道2的波形圖可以看到：微處理器對傳感器單脈沖預(yù)激振后,，傳感器輸出的頻率信號波形很微弱,、衰減快。此時經(jīng)過AD采樣,、傳統(tǒng)FFT計算出來的頻率f₀雖然十分接近傳感器的固有頻率,，但仍有一定的誤差。接下來對傳感器以頻率為f₀的PWM波復(fù)激振,，可以看到傳感器輸出信號的幅度很大,，持續(xù)時間長。此時再經(jīng)過AD采樣,、利用全相位FFT及Rife校正算法計算,，得到精準(zhǔn)度高的頻率值f。

3.2 系統(tǒng)測頻測試

    通過函數(shù)信號發(fā)生器將幅度為1 mV的正弦波接入系統(tǒng),，測得的數(shù)據(jù)如表1所示,。

    從表1可以看出，系統(tǒng)能夠以較高的精度實(shí)現(xiàn)微弱信號的頻率測量,，絕對誤差小于0.2 Hz,。

    將連接導(dǎo)線為10 m的振弦式傳感器接入系統(tǒng)，傳感器未施加外力,，系統(tǒng)放大倍數(shù)分別為400,、1 600的情況下，測量得到的數(shù)據(jù)如表2所示,。

    1#測量值是系統(tǒng)放大倍數(shù)為400時測量得到的數(shù)據(jù),，2#測量值是系統(tǒng)放大倍數(shù)為1 600時測量得到的數(shù)據(jù)。由表2可以看出,，由于傳感器的機(jī)械容差,，每次測量結(jié)果會稍有差異。同時,，放大倍數(shù)為400時測得的數(shù)據(jù)波動稍大,，且有一次測量錯誤，這主要是由于系統(tǒng)增益較低,，傳感器信號在預(yù)激振時幅度過小而無法正確計算頻率f0,，在復(fù)激振時由于f0偏離共振頻率較大,，從而無法使傳感器共振，導(dǎo)致系統(tǒng)測量出錯,。

4 結(jié)論

    本文以ARM處理器為核心,，采用全相位FFT算法對傳感器數(shù)據(jù)進(jìn)行預(yù)處理，再用Rife校正算法估計頻率,。實(shí)驗結(jié)果表明：系統(tǒng)的頻率測量絕對誤差小于0.2 Hz,。由此可見，采用全相位FFT-Rife校正算法可對振弦式傳感器實(shí)現(xiàn)精確的頻率測量,。

參考文獻(xiàn)

[1] 王秀麗,，馬潤田.大跨度鋼管桁架結(jié)構(gòu)全過程現(xiàn)場健康監(jiān)測研究[J].施工技術(shù)，2015(2)：54-57.

[2] 袁廣超,，徐振宇,，田旭東，等.多路振弦傳感器的掃頻激振技術(shù)[J].電子技術(shù)應(yīng)用,，2010(5)：26-28.

[3] 何華光,，謝忠杰，譚柳丹,，等.基于M-Rife算法的振弦式傳感器精確測頻系統(tǒng)設(shè)計[J].傳感器與微系統(tǒng),，2015(4)：69-71.

[4] 劉渝.快速高精度正弦波頻率估計綜合算法[J].電子學(xué)報，1999(6)：126-128.

[5] 齊國清,，賈欣樂.插值FFT估計正弦信號頻率的精度分析[J].電子學(xué)報,，2004(4)：625-629.

[6] 黃翔東，王兆華.全相位FFT相位測量法的抗噪性能[J].數(shù)據(jù)采集與處理,，2011(3)：286-291.

[7] RIFE D C,，VINCENT G A.Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J].Bell Syst.Tech.J.,，1970,，49：197-228.

[8] 黃翔東，王兆華．全相位時移相位差頻譜校正法[J]．天津大學(xué)學(xué)報,，2008,，41(7)：815-820．

[9] 賀虎，王萬順.振弦式傳感器激振策略優(yōu)化[J].傳感技術(shù)學(xué)報,，2010(1)：74-77.