0 引言

    擴(kuò)頻通信技術(shù)是一種十分重要的抗干擾通信技術(shù),，具有抗干擾能力強(qiáng),、可進(jìn)行多址通信、隱蔽性好,、抗多徑衰落等多種優(yōu)勢(shì),，在移動(dòng)通信、衛(wèi)星導(dǎo)航,、信號(hào)偵查與探測(cè)等領(lǐng)域都得到了廣泛的應(yīng)用^[1],。擴(kuò)頻序列是影響擴(kuò)頻通信系統(tǒng)性能的重要因素，近些年來,，混沌序列由于其初值敏感性,、類隨機(jī)特性、數(shù)量眾多等性質(zhì)^[2]在擴(kuò)頻通信系統(tǒng)中得到了廣泛的應(yīng)用,目前研究比較深入的有改進(jìn)型Logistic映射^[3],、Chebyshev映射^[4],、Tent映射^[5]等,。上述映射雖然擁有良好的類隨機(jī)特性和相關(guān)性，迭代公式簡(jiǎn)單,，工程上易于實(shí)現(xiàn),，但是均為一維單級(jí)迭代映射，結(jié)構(gòu)簡(jiǎn)單,，生成的混沌序列復(fù)雜度不夠高,，通過相空間重構(gòu)、反向迭代等方法被破譯的可能性較大^[6],。因此本文提出了一種通過迭代級(jí)聯(lián)混沌映射構(gòu)造新型擴(kuò)頻序列的方法,，將迭代方程的輸入輸出值在不同的單級(jí)混沌映射間切換，在反復(fù)迭代的過程中改善了系統(tǒng)的動(dòng)力學(xué)特性,，擴(kuò)展了系統(tǒng)的密鑰空間,，增加了混沌序列的復(fù)雜度，更有利于提高擴(kuò)頻通信系統(tǒng)的安全保密性,。

1 迭代級(jí)聯(lián)混沌映射

1.1 迭代級(jí)聯(lián)混沌映射的提出

    改進(jìn)型Logistic混沌映射定義為^[3]：

    當(dāng)初始值x₀∈(-1,，1)，分型參數(shù)μ=2時(shí),，系統(tǒng)處于混沌狀態(tài),，并且為滿映射。

    Chebyshev混沌映射定義為^[4]：

    初始值x₀∈(-1,，1),，ω為映射的階數(shù)，當(dāng)ω=2ⁿ時(shí),，系統(tǒng)處于混沌狀態(tài),。

    考慮到改進(jìn)型Logistic混沌映射和Chebyshev混沌映射具有相同的取值范圍和相同的概率密度分布函數(shù)，為了提高混沌系統(tǒng)的復(fù)雜度和安全性,，可將上述兩種映射通過迭代級(jí)聯(lián)的方法構(gòu)造出一種新型混沌映射,，將一個(gè)混沌映射的輸出作為另一個(gè)混沌映射的初值并進(jìn)行反復(fù)迭代^[7]。每次迭代在兩種單級(jí)混沌映射中隨機(jī)選擇一種,，當(dāng)映射總迭代次數(shù)為N時(shí),，整個(gè)混沌系統(tǒng)共有2^N種不同的混沌映射組合方式，大大提高了混沌系統(tǒng)的密鑰空間,。由于每次迭代的初值在不同的混沌映射中切換,，有效提高了相空間軌道的模糊性，進(jìn)一步提高了混沌系統(tǒng)的復(fù)雜度,、保密性,、安全性。當(dāng)每次迭代都選擇同一種混沌映射時(shí)，迭代級(jí)聯(lián)混沌映射將退化為普通的單級(jí)映射,，此時(shí)改進(jìn)型Logistic混沌映射和Chebyshev混沌映射成為新型混沌映射的兩種特殊形式,。

    鑒于迭代級(jí)聯(lián)混沌映射組合方法多達(dá)2^N種，難以逐一分析,，本文針對(duì)其中一種映射交替迭代的特殊情況進(jìn)行分析,。新型混沌映射數(shù)學(xué)表達(dá)式如下：

    給定初值x₀后，迭代公式在兩種單級(jí)混沌映射中交替切換,，每次迭代的結(jié)果由兩種單級(jí)混沌映射的相關(guān)參數(shù)和迭代次數(shù)共同決定,，大大提高了混沌系統(tǒng)的復(fù)雜度和安全性，下面對(duì)該新型混沌映射的性質(zhì)進(jìn)行分析,。

1.2 新型混沌映射遍歷性分析

    分岔圖可以清楚地反映出分形參數(shù)μ與混沌映射離散數(shù)值分布的關(guān)系^[6],。圖1中給出了改進(jìn)型Logistic混沌映射和新型混沌映射的分岔圖。

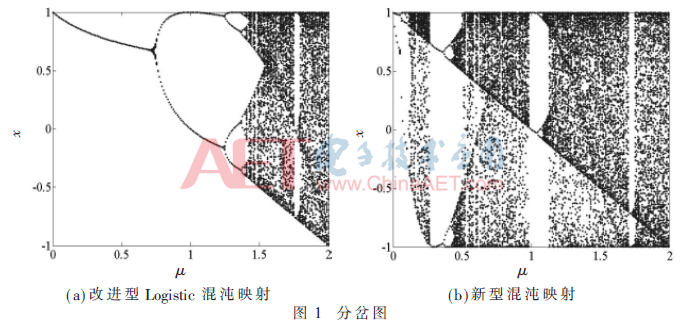
    由圖1可以看出對(duì)于改進(jìn)型Logistic混沌映射,，只有在分形參數(shù)μ=2時(shí),，迭代結(jié)果才會(huì)映射在整個(gè)[-1，1]區(qū)間,，這種狀態(tài)被稱作滿映射狀態(tài),。當(dāng)分形參數(shù)取其他數(shù)值時(shí)，混沌序列迭代數(shù)值范圍縮小,，數(shù)值分布集中,，系統(tǒng)的遍歷性和隨機(jī)性降低。而本文提出的新型混沌映射擴(kuò)展了滿映射狀態(tài)的分布區(qū)間,，使分形參數(shù)μ的可選取范圍大大增加,，這進(jìn)一步擴(kuò)展了混沌系統(tǒng)的密鑰空間，系統(tǒng)安全性,、保密性能得到提升,。

2 混沌序列性能分析

2.1 混沌序列的數(shù)字量化

    為了將混沌映射產(chǎn)生的實(shí)值序列應(yīng)用到擴(kuò)頻通信系統(tǒng)中，需要對(duì)實(shí)值序列進(jìn)行數(shù)字量化處理,，將實(shí)值序列轉(zhuǎn)化為二進(jìn)制序列,。二值量化法是一種最常見的數(shù)值量化方法，其核心思想是尋找一個(gè)判決門限T,，將序列數(shù)值與門限T比較,，方法如下式：

    二值量化法原理簡(jiǎn)單，但是判決門限T的選擇將影響到混沌擴(kuò)頻序列的平衡性,，擴(kuò)頻序列的平衡性反映了二進(jìn)制序列中1與-1數(shù)量的均勻程度，其定義式為:

其中U與V分別表示序列中1與－1的數(shù)目,，N表示序列長(zhǎng)度,。混沌序列的平衡性與載波抑制度有密切的關(guān)系，低平衡性的混沌序列會(huì)導(dǎo)致直擴(kuò)系統(tǒng)的載漏增大,，將破壞擴(kuò)頻系統(tǒng)保密性,、抗干擾和抗偵破的能力^[8]。選擇合適的判決門限,，提高序列的平衡性對(duì)提升擴(kuò)頻通信系統(tǒng)的性能有重要的意義,。下面對(duì)迭代級(jí)聯(lián)混沌映射的判決門限進(jìn)行分析。

    由圖1可以看出,，雖然保證數(shù)值分布為滿映射的分形參數(shù)μ的取值范圍大大增加,，但當(dāng)分形參數(shù)μ=2時(shí)混沌映射數(shù)值分布更加均勻，有更良好的隨機(jī)性,，因此在新型混沌映射模型式(5)中,，設(shè)置相關(guān)參數(shù)μ=2，ω=4,，迭代次數(shù)10 000次,，對(duì)其數(shù)值在[-1，1]區(qū)間上的分布情況進(jìn)行統(tǒng)計(jì),，統(tǒng)計(jì)結(jié)果如圖2所示,。

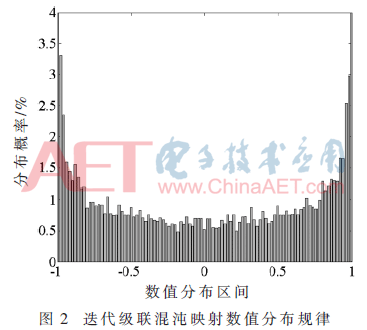
    由圖2可以看出在給定參數(shù)下，新型混沌映射的數(shù)值分布規(guī)律與構(gòu)成新型混沌映射的兩個(gè)子映射的概率密度分布函數(shù)類似,，兩邊高,、中間窄，近似關(guān)于x=0成軸對(duì)稱分布,，因此可以選取T=0作為新型混沌映射的判決門限,。

2.2 平衡性分析

    下面分析新型混沌序列二值化后的平衡性。隨機(jī)選取50個(gè)不同的初值,，計(jì)算平衡性的平均值并繪出曲線,，結(jié)果如圖3所示?？梢钥闯鲭S著序列的長(zhǎng)度增加,，序列的平衡性越來越好，新型混沌序列的平衡性優(yōu)于改進(jìn)型Logistic混沌序列和Chebyshev混沌序列,。

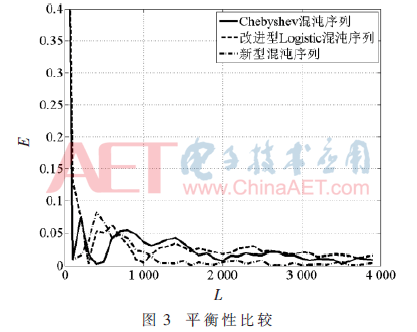
2.3 復(fù)雜度分析

    有限長(zhǎng)序列的復(fù)雜度是指它與隨機(jī)序列的相似程度,，可以在一定程度上反映出通信系統(tǒng)的保密性能和抗截獲性能。傳統(tǒng)偽隨機(jī)擴(kuò)頻序列的復(fù)雜度通常采用Berlekamp-Massey算法進(jìn)行衡量,，但該算法是一種計(jì)算線性復(fù)雜度的算法,，有較大的局限性，并不適合用來衡量混沌序列的復(fù)雜度^[9],。文獻(xiàn)[10]提出了一種通過近似熵（ApEn）算法來衡量混沌擴(kuò)頻序列復(fù)雜度的方法,，該算法通過描述序列維數(shù)增加時(shí)混沌軌道的分離程度來衡量混沌序列的復(fù)雜度,，物理意義清晰，計(jì)算方法簡(jiǎn)單易實(shí)現(xiàn),，其計(jì)算步驟如下：

    (1)混沌序列長(zhǎng)度為N,，以序列值域?yàn)闃颖镜玫絅點(diǎn)數(shù)據(jù)a(1)，a(2),，…,，a(N)。

    (2)構(gòu)造m維向量組：

    (5)定義近似熵(ApEn)為：

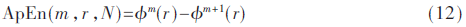
    ApEn數(shù)值越大,，混沌序列的復(fù)雜度越高,。上述參數(shù)中m通常取1或2，r通常取0.1~0.25倍樣本數(shù)據(jù)的標(biāo)準(zhǔn)差^[9],。

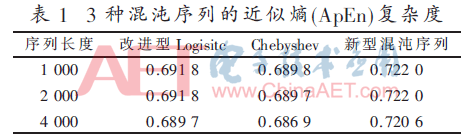
    下面對(duì)經(jīng)過二值化的新型混沌序列,、Logistic混沌序列、Chebyshev混沌序列三者的ApEn進(jìn)行仿真計(jì)算,，計(jì)算參數(shù)為N分別取1 000,、2 000、4 000,，r取0.12,，m取2，計(jì)算結(jié)果如表1所示,。由表1可以看出新型混沌序列的復(fù)雜度最高,，改進(jìn)型Logisitc混沌序列次之，Chebyshev混沌序列復(fù)雜度最低,。這也證實(shí)了本文提出用迭代級(jí)聯(lián)混沌映射構(gòu)造的新型混沌序列確實(shí)具有更高的復(fù)雜度,，更有利于提高通信系統(tǒng)的保密性和抗截獲性。

2.4 相關(guān)性分析

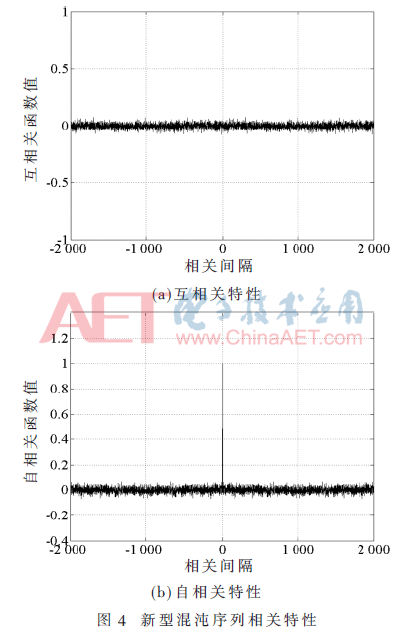
    相關(guān)性是衡量擴(kuò)頻序列性能的重要指標(biāo),，與擴(kuò)頻通信系統(tǒng)的抗干擾能力和抗多址能力密切相關(guān),。理想的擴(kuò)頻序列應(yīng)該具備類似白噪聲一樣尖銳的自相關(guān)函數(shù)，和處處為零的互相關(guān)函數(shù)^[11],。理論上無限長(zhǎng)混沌序列可以滿足上述性質(zhì),，但在實(shí)際應(yīng)用中混沌序列不可能取到無限長(zhǎng)，要經(jīng)過截短處理后才能使用,，這在一定程度上破壞了混沌序列的相關(guān)特性,。圖4顯示一個(gè)初值為x=0.1，參數(shù)設(shè)定為μ=2,，ω=4,，序列長(zhǎng)度為2 000的新型混沌序列自相關(guān)函數(shù)值和互相關(guān)函數(shù)值的分布情況，從圖中可以看出新型混沌序列的自相關(guān)函數(shù)值有尖銳的相關(guān)峰,，自相關(guān)函數(shù)旁瓣值和互相關(guān)函數(shù)值均接近于零,表明新型混沌序列有良好的相關(guān)性能,。

3 擴(kuò)頻通信仿真

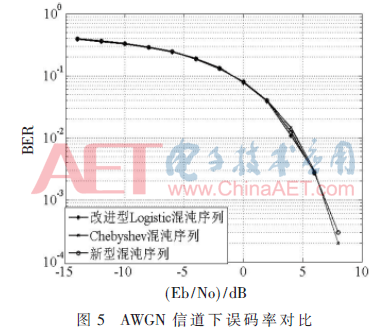
    為了進(jìn)一步驗(yàn)證本文提出的新型迭代級(jí)聯(lián)混沌擴(kuò)頻序列的性能,通過MATLAB軟件對(duì)3種混沌序列進(jìn)行擴(kuò)頻通信仿真,。仿真條件設(shè)定序列碼長(zhǎng)1 024,，信噪比取值范圍是[-15 dB,，10 dB]，調(diào)制方式為BPSK,，混沌序列參數(shù)選取μ=2,、ω=4，每種混沌序列隨機(jī)選取1 000個(gè)初值設(shè)并計(jì)算誤碼率平均值,經(jīng)過AWGN信道后誤碼率曲線如圖5所示,。由圖5可以看出3種混沌序列在理想高斯白噪聲信道下誤碼率曲線相互交叉,，基本重合，誤碼率性能相當(dāng),。

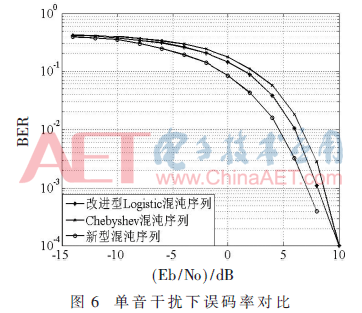
    下面考慮AWGN信道中加入干擾信號(hào)的情況,，仿真條件不變，在高斯信道中加入單音干擾信號(hào),，誤碼率曲線如圖6所示,，圖中可以看出新型混沌序列的誤碼率明顯低于改進(jìn)型Logistic混沌序列和Chebyshev混沌序列，說明新型混沌序列相對(duì)于其他兩種混沌序列具有更強(qiáng)的抗干擾能力,。

4 結(jié)論

    本文在改進(jìn)型Logistic混沌映射和Chebyshev混沌映射的基礎(chǔ)上提出了一種新型迭代級(jí)聯(lián)混沌映射,。其組合方式多樣，迭代方程由多個(gè)參數(shù)共同決定,，有效提高了混沌系統(tǒng)的復(fù)雜度和安全性,。通過對(duì)該映射進(jìn)行遍歷性分析，發(fā)現(xiàn)其滿映射分布區(qū)間更廣,，隨機(jī)性能更好,。對(duì)新型混沌序列二值化判決門限的選取進(jìn)行了分析，仿真對(duì)比驗(yàn)證3種混沌序列的平衡性,、復(fù)雜度和相關(guān)性,，結(jié)果表明，本文提出的新型混沌序列復(fù)雜度高,，具有良好的相關(guān)性和平衡性,，抗干擾能力更強(qiáng)，更加適用于擴(kuò)頻通信系統(tǒng)中,。

參考文獻(xiàn)

[1] 暴宇,，李新民.擴(kuò)頻通信技術(shù)及應(yīng)用[M].西安：西安電子科技大學(xué)出版社，2011.

[2] 劉嘉興,，何世彪.混沌測(cè)控的概念,、特性與實(shí)現(xiàn)[J].飛行器測(cè)控學(xué)報(bào)，2011,，30(1)：1-5.

[3] 王亥,，胡健棟.改進(jìn)型Logistic-Map混沌擴(kuò)頻序列[J].通信學(xué)報(bào),，2007，28(2)：134-140.

[4] 雷利華,，馬冠一,，蔡曉靜，等.基于Chebyshev映射的混沌序列研究[J].計(jì)算機(jī)工程,，2009,，35(24)：1-3.

[5] 劉金梅，張衛(wèi),，丘水生.一種改善Tent混沌序列隨機(jī)性的方法[J].計(jì)算機(jī)工程,，2012，38(24)：10-12.

[6] 李雙鑫,，王馳,，李廣喆，等.一種新型的二級(jí)分段Logistic混沌映射及其性能分析[J].東北師大學(xué)報(bào)(自然科學(xué)版),，2014,，45(4)：82-87.

[7] 李長(zhǎng)庚，周家令,，孫克輝,，等.基于M序列同步的混沌擴(kuò)頻通信系統(tǒng)研究與仿真[J].系統(tǒng)仿真學(xué)報(bào)，2009,21(4)：1198-1201.

[8] 羅冬梅.混沌序列特性分析及同步技術(shù)研究[D].重慶：重慶大學(xué),，2011.

[9] 蔡覺平,，李贊，宋文濤.一種混沌偽隨機(jī)序列復(fù)雜度分析法[J].物理學(xué)報(bào),，2003,，52(8)：1871-1876.

[10] PINCUS S M.Approximate entropy as a measure of system　complexity[J].Proceedings of the National Academy of Science，1991,，88(6)：2297-2301.

[11] 余振標(biāo),，馮久超.一種混沌擴(kuò)頻序列的產(chǎn)生方法及其優(yōu)選算法[J].物理學(xué)報(bào)，2008,，57(3)：1409-1415.