0 引言

　　隨著電路板制造工藝的發(fā)展,，電子元器件的集成度越來越高，電路越來越復(fù)雜，傳統(tǒng)接觸式診斷故障需要大量的時(shí)間和精力,，紅外成像對故障診斷方法已經(jīng)成為目前重要方法[1-2],，但是電路板紅外成像的比度差、動態(tài)范圍小,、圖像模糊,，因此需要對電路板紅外成像增強(qiáng)。

　　目前電路板紅外成像增算法有：基于直方圖變換的電路板紅外成像增強(qiáng)[3],，其亮度較高,，噪聲較大，細(xì)節(jié)不明顯,；基于灰度變換的電路板紅外成像增強(qiáng)[4],，其亮度均勻，細(xì)節(jié)明顯,，噪聲小但整體偏暗,；基于Retinex方法的電路板紅外圖像增強(qiáng)[5]，其可提高視覺效果,，但是對光照變化相當(dāng)敏感,；同態(tài)濾波增強(qiáng)算法，其適合較好對比度的紅外圖像[6],，對大部分紅外圖像經(jīng)過同態(tài)濾波處理之后圖像灰度會更低,，圖像對比度會更差。

　　為了提高電路板紅外成像增強(qiáng)的效果,，本文采用量子行為粒子優(yōu)化算法,。在量子空間中更新粒子位置，建立粒子停滯系數(shù)與收縮擴(kuò)張系數(shù)之間的關(guān)系,，通過判斷粒子停滯有效地減少無效迭代,，并采用非完全Beta函數(shù)實(shí)現(xiàn)電路板紅外圖像增強(qiáng)。實(shí)驗(yàn)仿真顯示本文算法對電路板紅外成像細(xì)節(jié)增強(qiáng)效果比較清晰,，均方誤差明顯減小,，相對信噪比明顯提高。

1 量子行為優(yōu)化粒子群算法

　　由于在量子空間中不能同時(shí)確定粒子的速度和位置,，位置是唯一描述粒子狀態(tài)的變量[7],，因此在量子行為優(yōu)化粒子群算法中粒子的位置方程為:

　　其中：xi(t)為第i個(gè)粒子第t次迭代的位置，為收縮擴(kuò)張系數(shù),，向量pi=(pi1,，pi2，…piD)是第i個(gè)粒子的歷史最佳位置,，D為空間維數(shù),，為[0，1]之間的隨機(jī)數(shù)，c(t)表示所有粒子個(gè)體極值的平均值,，c(t)為：

　　其中：m為粒子個(gè)數(shù),；i=1，2,，…,，m；D=1,，2,，…，n,。

　　在迭代中,，將每一個(gè)粒子當(dāng)前位置的適應(yīng)值與全局最好位置的適應(yīng)值進(jìn)行對比[8-9]，當(dāng)前者較好時(shí),，從全局最好位置開始更新,。在k維空間中第i個(gè)粒子第t次迭代時(shí)的適應(yīng)值方程gik(t)為：

　　其中：(t)∈(0，1),，pik(t)為個(gè)體最好位置,，gk(t)為群體最好位置。

　　量子行為優(yōu)化粒子群算法使粒子的狀態(tài)只需用位置向量進(jìn)行描述即可,，且算法中只有一個(gè)控制參數(shù),，值越大，粒子搜索范圍越廣,，過大會降低算法收斂速度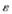,；值越小，粒子會在局部仔細(xì)搜索,，過小會使算法陷入局部收斂,；合適的能夠使得全局搜索和局部搜索全面進(jìn)行，從而找到全局最優(yōu)解,。

　　通過停滯系數(shù)判定算法是否陷入停滯：

　　其中：t′為種群最優(yōu)個(gè)體的適應(yīng)值連續(xù)不變的迭代次數(shù),，即若連續(xù)t′代最優(yōu)個(gè)體的適應(yīng)值沒有變化，則種群停滯系數(shù)就為,。

　　因此,，選擇一個(gè)與成正比的動態(tài)?著：

　　其中：調(diào)整后若算法適應(yīng)值變優(yōu)，則歸零,；若適應(yīng)值未變優(yōu)，則繼續(xù)調(diào)整,。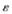

2 電路板紅外圖像增強(qiáng)過程

　　2.1 非完全Beta函數(shù)實(shí)現(xiàn)電路板紅外圖像增強(qiáng)

　　采用非完全Beta函數(shù)來實(shí)現(xiàn)電路板紅外圖像的增強(qiáng)[10],，歸一化的非完全Beta函數(shù)F(u)定義為：

　　其中：B(?琢，?茁)為Beta函數(shù)，Beta表示為：

　　其中：當(dāng)<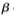時(shí),，所得變換函數(shù)對較暗區(qū)域進(jì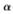n)行拉伸,；當(dāng)=時(shí)，變換曲線是對稱的,，對中間區(qū)域進(jìn)行拉伸,；當(dāng)>時(shí)，經(jīng)過變換后對較亮的區(qū)域進(jìn)行拉伸,。

　　一幅大小為(M×N),，具有L級灰度的圖像I={f(x，y)},，f(x,，y)∈{Lmin，Lmin+1,，Lmin+2,，…，Lmax},，Lmin與Lmax滿足Lmax-Lmin∈[63,，126],。為增強(qiáng)方便，將f(x，y)進(jìn)行歸一化為f′(x,，y)：

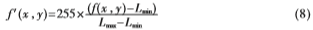
　　其中：Lmax、Lmin分別為處理圖像灰度的最大值和最小值,。求解出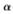和最優(yōu)取值,，即可實(shí)現(xiàn)電路板紅外圖像的增強(qiáng)，圖像增強(qiáng)質(zhì)量評價(jià)函數(shù)作為量子行為粒子優(yōu)化算法的適應(yīng)度函數(shù)：

　　其中：M,、N分別為圖像的寬和高,；n=M×N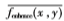；為增強(qiáng)后圖像fenhence(x,，y)的灰度均值,。fitness(f，,，)值越大,，則圖像灰度分布越均勻，圖像對比度越高,，圖像質(zhì)量越好,。

　　2.2 算法流程

　　(1)輸入待增強(qiáng)圖像，初始化圖像灰度值,；

　　(2)按式(1)更新粒子的個(gè)體最優(yōu)位置,，按式(3)計(jì)算粒子i的當(dāng)前位置xi(t)的適應(yīng)度函數(shù)值,，即將xi(t)的適應(yīng)度函數(shù)值與前一次迭代的粒子的個(gè)體最優(yōu)位置pik(t-1)的適應(yīng)度函數(shù)值比較，如果xi(t)的適應(yīng)度函數(shù)值優(yōu)于pik(t-1)的適應(yīng)度函數(shù)值,，則pik(t)=xi(t),；否則pik(t)=pik(t-1)；

　　(3)將粒子i個(gè)體最優(yōu)位置pik(t)的適應(yīng)度函數(shù)值與全局最優(yōu)位置gk(t)的適應(yīng)度函數(shù)值比較,，pik(t)優(yōu)于gk(t-1),，則pik(t)=gk(t)；否則gk(t)=gk(t-1),；

　　(4)更新粒子i位置xi(t+1)計(jì)算獲得的(,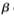，)，按式(9)判斷適應(yīng)度,，若連續(xù)個(gè)新解都沒有被接受,，則終止尋優(yōu)，進(jìn)行步驟(5),；否則進(jìn)行步驟(2),；

　　(5)將增強(qiáng)后的圖像反歸一化處理，得到輸出圖像,。

3 實(shí)驗(yàn)仿真

　　3.1 視覺仿真

　　實(shí)驗(yàn)PC配置為CPU3.6 GHz,、內(nèi)存2 GB、IntelH61主板,、集成顯卡,，采用MATLAB7.0編程實(shí)現(xiàn)仿真，電路板紅外圖像進(jìn)行各種算法的對比增強(qiáng)效果如圖1所示,。

　　從圖1的對比結(jié)果中可以看出,，量子行為粒子優(yōu)化算法對電路板紅外成像增強(qiáng)了對比度，圖像亮度得到了整體提升,，細(xì)節(jié)比較清晰,；直方圖方法增強(qiáng)效果中細(xì)節(jié)不明顯；灰度變換方法增強(qiáng)效果整體偏暗,；Retinex方法增強(qiáng)效果中,，發(fā)熱小的芯片受到背景區(qū)域的影響非常大，甚至與背景相混淆,，增加了直觀定位故障的難度,；同態(tài)濾波方法增強(qiáng)效果中圖像對比度較差。

　　3.2 指標(biāo)分析

　　為了綜合分析本文算法對電路板紅外圖像增強(qiáng)的客觀評價(jià)效果,，采用的指標(biāo)如下,。

　　(1)均方誤差(Mean Squared Error，MSE)：

　　其中：f(m,，n)為原始圖像,，是增強(qiáng)后的圖像,，M,、N為圖像矩陣的行,、列總數(shù)。

　　(2)相對信噪比(Relative Signal to Noise Ratio,，RSNR),，指增強(qiáng)后的紅外圖像相對于原始圖像的信噪比，主要衡量增強(qiáng)圖像相對于原始圖像去除噪聲的能力：

　　對圖1(a)待增強(qiáng)電路板紅外成像進(jìn)行20次蒙特卡羅仿真實(shí)驗(yàn),，然后取其均值,，各種算法的MSE指標(biāo)分析如圖2(a)所示，RSNR指標(biāo)分析如圖2(b)所示,。

　　從圖2的數(shù)據(jù)指標(biāo)分析可以發(fā)現(xiàn),，本文算法相比其他方法有了很大的改善，均方誤差MSE明顯減小了,，相對信噪比RSNR明顯提高了,，因此電路板的紅外成像質(zhì)量有了明顯的增強(qiáng)。

(a)各種算法的MSE指標(biāo)分析

(b)各種算法的RSNR指標(biāo)分析

4 結(jié)論

　　在量子空間中更新粒子位置,，建立粒子停滯系數(shù)與收縮擴(kuò)張系數(shù)之間的關(guān)系,，有效地減少無效迭代；非完全Beta函數(shù)實(shí)現(xiàn)電路板紅外圖像增強(qiáng),。實(shí)驗(yàn)仿真顯示本文算法對電路板紅外成像細(xì)節(jié)增強(qiáng)效果比較清晰,，均方誤差明顯減小，相對信噪比明顯提高,，為電路板紅外成像增強(qiáng)提供了一種新方法,。

　　參考文獻(xiàn)

　　[1] 郝建新.基于小波變換與Retinex的電路板紅外圖像增強(qiáng)技術(shù)[J].紅外技術(shù)，2015,，37(12)：1036-1040.

　　[2] 崔昊楊,，許永鵬，楊俊杰,，等.基于MIV和BRBP神經(jīng)網(wǎng)絡(luò)的電路板紅外診斷方法[J].激光與紅外,，2014，44(4)：382-386.

　　[3] HASEGAWA M,，TABBONE S.Histogram of Radon transform with angle correlation matrix for distortion invariant shape descriptor[J].Neurocomputing,，2016，15(1)：24-35.

　　[4] Li Tiangang,，Wang Supin,，Zhao Nan.Gray-scale edge detection for gastric tumor pathologic cell images by morphological analysis[J].Computers in Biology and Medicine，2009,，39(11)：947-952.

　　[5] Wang Guodong,，Dong Qian,，Pan Zhenkuan，et al.Retinex theory based active contour model for segmentation of inhomogeneous images[J].Digital Signal Processing,，2016,，50(3)：43-50.

　　[6] SHARMA H，SHARMA K K,，BHAGAT O L.Respiratoryrate extraction from single-lead ECG using homomorphic filtering[J].Computers in Biology and Medicine,，2015，59(1)：80-86.

　　[7] 焦鵬,，王新政,，謝鵬遠(yuǎn).基于量子行為粒子群算法的可測試性設(shè)計(jì)方法[J].艦船電子工程，2013,，33(3)：105-107.

　　[8] 張宏立,，李瑞國，范文慧,，等.基于量子粒子群的全參數(shù)連分式混沌時(shí)間序列預(yù)測[J].控制與決策,，2016，31(1)：52-58.

　　[9] 肖文顯,，王俊閣,，馬孝琴.自適應(yīng)調(diào)整差分進(jìn)化算法在優(yōu)化問題中的應(yīng)用[J].哈爾濱理工大學(xué)學(xué)報(bào)，2015,，20(1)：71-74.　

　　[10] 李欣然,，靳雁霞.量子行為粒子群優(yōu)化算法在公交調(diào)度優(yōu)化中的應(yīng)用[J].計(jì)算機(jī)系統(tǒng)應(yīng)用，2012,，21(7)：191-195.