滿蔚仕,馮亞平,張志禹

　?。ㄎ靼怖砉ご髮W(xué) 自動化與信息工程學(xué)院 ，陜西 西安710048）

       摘要：提出了一種故障分支判別的新判據(jù)和故障測距的新方法,。故障分支判別充分利用雙端行波定位原理和三端行波量測數(shù)據(jù),，考慮了測距誤差因素對分支誤判情況的影響，確保分支判別的有效性,；故障點的測距通過對三端故障電壓行波進行TT變換,，然后提取信號TT變換模矩陣的對角線元素序列，利用TT變換對角線元素的頻譜特性,，精確標(biāo)定行波波頭到達量測點的時刻,。MATLAB仿真結(jié)果表明，該方法正確可行,，具有較高的測距精度,，且在較大的環(huán)境干擾下可以實現(xiàn)T型線路的分支判別和故障測距。

　　關(guān)鍵詞：T型線路,；行波,；故障測距；TT變換

0引言

　　輸電線路故障測距一直是電力系統(tǒng)的研究熱點,。隨著電力系統(tǒng)的不斷發(fā)展,，T型輸電線路因其輸送功率大等特點在高壓輸電線路中的應(yīng)用變得越來越廣泛。對T型線路故障測距算法的研究也越來越受到關(guān)注,。T 型線路的故障測距主要分為兩大類：故障分析法和行波法。故障分析法易受過渡電阻等因素的影響，測距精度不高,，因此行波法是目前研究的熱點,。

　　目前，國內(nèi)外學(xué)者針對T型線路行波測距已經(jīng)提出了多種故障定位方法［12］,。文獻［2］和文獻［3］首先利用雙端行波原理進行故障分支判別,，然后進行精確的故障測距。文獻［4］利用現(xiàn)有的兩端測距公式推導(dǎo)出了三端測距公式,，在故障點的測距過程中消除了波速對測距結(jié)果的影響,。文獻［3］消除了波速對定位結(jié)果的影響，但需要通過波速來判斷故障分支,。

　　TT變換是近年來出現(xiàn)的一種時時分析方法,。TT變換源于S變換，S變換是短時傅里葉變換和連續(xù)小波變換的延伸,。TT變換［5］在2003年由PINNEGAR C R等人首先提出,，是一維時間序列的二維實時表示，具有很強的局部時間分析能力,，目前TT變換在電能質(zhì)量檢測中取得了良好的效果,，應(yīng)用于故障診斷分析則較少。

　　本文提出了T型線路故障分支判別的新判據(jù)和故障測距的新方法,。先通過三端量測數(shù)據(jù)對T型線路進行故障分支判別,，再對相模變換后的故障電壓行波進行TT變換，得到TT模矩陣,，檢測TT模矩陣對角線元素的幅值突變點即行波首波頭到達量測點的精準(zhǔn)時刻,。該方法只需獲取行波首波頭的到達時刻，不需考慮行波折反射,，能在T節(jié)點附近發(fā)生故障時正確判別故障分支并進行精確的故障測距,。

1故障分支判別及測距

如圖1所示,以PT段發(fā)生單相短路故障為例說明分支的判別方法。當(dāng)M點發(fā)生單相接地短路故障時,輸電線路產(chǎn)生故障電壓行波并以接近光速的速度向三端傳播,。

　　故障分支判別由以下公式計算：

　　式中,，lij是兩個量測端的線路長度，ti是行波到達量測端的時間,，v是行波波速,。故障分支的判據(jù)為：若dRT≤lRP且dRS≤lRP，則故障在RP支路,；若dRS>lRP且dST<lSP,，則故障在SP支路；若dRT>lRP且dST≥lSP,，則故障在TP支路,。

　　故障分支判別后進行測距,。故障在RP支路時，dRM=dRT+dRS/2,；故障在SP支路時,，dSM=(lRS-dRS)+dST/2；故障在TP支路時,，dTM=(lRT-dRT)+(lST-dST)/2,。

2TT變換檢測行波首波頭到達時刻

　　2.1TT變換及其對角線元素分析

　　信號的S變換定義為：

　　S變換的窗函數(shù)定義為：

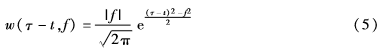
　　對S變換進行傅里葉逆變換，就得到TT變換：

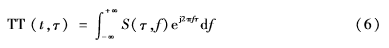
　　TT變換對角線元素定義為［6］：

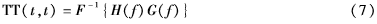
　　式中,，F(xiàn)-1為傅里葉逆變換,，H(f)為信號h(t)的傅里葉變換；G(f)由積分變換可得：

　　式中pk(1)是常量,，k=tτ,，p1(1)-0.021 99，p3(1)-0.006 79,，p5(1)-0.004 05,。

　　式(8)表明，G(f)與|f|成正比,，|f|越大,，G(f)越大，即對角線元素值越大,，因此在t=τ時,，信號的高頻部分比低頻部分的振幅更高。輸電線路短路故障會產(chǎn)生高頻分量,，因而可用TT變換來精確定位行波首波頭的到達時刻,。

　　2.2故障行波首波頭到達時刻檢測

　　本文選取三端故障電壓行波作為量測量。先截取故障前后三端母線的故障電壓行波,，然后利用Clark變換對其進行解耦,，選取解耦后的α模電壓分量進行故障測距研究。

　　當(dāng)T型線路某處發(fā)生短路故障時,，線路中將產(chǎn)生故障行波,。對α模電壓分量進行TT變換得到TT模矩陣，提取模矩陣對角線序列,。對角線序列中模最大值對應(yīng)的采樣時刻即為故障電壓行波首波頭到達該量測點的時刻,。

　　假設(shè)輸電線路某處發(fā)生單相短路故障，故障電壓經(jīng)Clark變換后得到故障前后一段時間的α模電壓波形,，如圖2所示,。

　　由圖2可知，α模分量出現(xiàn)大的波動,，但不確定精確時間,。對圖2行波進行TT變換并提取TT變換對角線元素確定行波首波頭的精確到達時刻,。圖3為對角線元素序列幅-時圖。

　　由圖3可見,，模最大值對應(yīng)的采樣時刻為176個采樣點處,。因此，TT變換對角線元素序列中模最大值對應(yīng)的時刻即為行波首波頭的到達時刻,。大量仿真結(jié)果證明，此方法能夠精確檢測行波首波頭的到達時刻,。

3仿真分析

　　為驗證方法的有效性,，對單回T型線路進行仿真。線路模型如圖1,。線路長度lRP,、lSP、lTP分別為100 km,、150 km,、200 km。線路的正序和零序參數(shù)為r1=0.012 73 Ω/km,，L1=0.933 7 mH/km,，C1=0.012 74 μF/km；r0=0.386 4 Ω/km,，L0=4.126 4 mH/km,，C0=0.007 75 μF/km。系統(tǒng)3端電源E·R,、E·S,、E·T電動勢為500 kV，初始相位角分別為0°,、30°,、60°。信號仿真的采樣頻率為1 MHz,，根據(jù)線路參數(shù),，波速度v=289 950 km/s。

　　仿真算例1：線路TP區(qū)間距離T端100 km處,，t=0.035 s時發(fā)生A相短路故障,，接地電阻和過渡電阻均為50 Ω，考慮到實際運用,，各電壓信號均加入40 db的高斯白噪聲,。圖4中（a）、（b）,、（c）分別為R,、S,、T量測端測得的故障電壓行波，經(jīng)過TT變換如圖5（a）,、（b）,、（c）?？蓽y得行波首波頭到達三端的采樣時間分別為693,、866、348個采樣點,即tR=0.000 693 s,、tS=0.000 866 s,、tT=0.000 348 s,代入公式（1）、（2）,、（3）,，可得dRS=99.919 3 km、dRT=225.097 1 km,、dST=225.016 4 km,。滿足TP故障的判定條件，判定TP支路發(fā)生故障,。由上述測距公式可得dTM=99.943 2 km,，誤差為56 m。

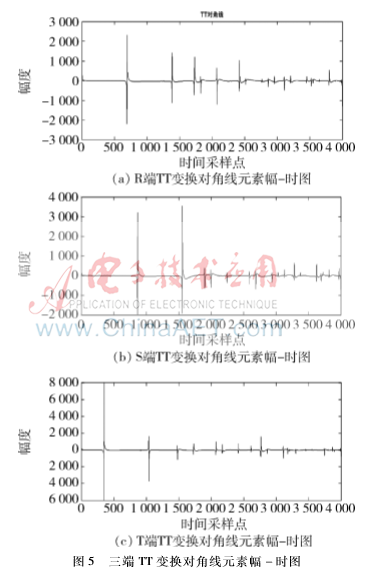
　　仿真算例2：P節(jié)點故障,。假設(shè)RP支路距R端99.5 km處,，t=0.035 s時發(fā)生A相短路故障，接地電阻為200 Ω,，過渡電阻為50 Ω,。同理可得行波首波頭到達三端的時間分別為346、523,、695采樣點,即tR=0.000 346 s,、tS=0.000 523 s、tT=0.000 695 s,代入公式（1）,、（2）,、（3），可得dRS=99.339 4 km,、dRT=99.403 7 km,、dST=150.064 3 km。滿足RP分支故障的判定條件,，判定RP支路發(fā)生故障,。由上述測距公式可得dRM=99.371 6 km，誤差為128 m,。采用本方法克服了傳統(tǒng)缺陷,，在P節(jié)點附近0.5 km還能正確判別故障支路,，確定故障位置，無測距死區(qū),，測距精度高,。

　　表1列出了在加入40 db的高斯白噪聲干擾下，發(fā)生各種故障時本文方法的測距結(jié)果,。由表1可知,，本文方法在T型線路各支路范圍內(nèi)都可以測距，測距精度很高,。

　　表2列出了不同過渡電阻下本文的測距結(jié)果,，設(shè)故障點在TP支路上。由表2可知,，本文方法基本不受過渡電阻影響，當(dāng)過渡電阻很大時,，還能達到很高的測量精確度,。

4結(jié)論

　　本文在行波測距基礎(chǔ)上, 對T型線路的故障測距進行了研究, 提出了分支判別的新判據(jù)和故障測距的新方法，通過TT變換對角線元素序列的譜分析,，精確捕捉行波波頭到達量測端的時刻,。并對T節(jié)點附近發(fā)生短路故障進行了研究，傳統(tǒng)方法在T節(jié)點附近故障時無法正確判別故障分支,，采用本文方法可以正確判別故障分支,。MATLAB仿真結(jié)果表明本文方法的有效性，并且不受故障類型,、故障距離和過渡電阻的影響,，有一定的抗干擾能力，具有一定的實際應(yīng)用價值,。

　　參考文獻

　?。?］ 李傳兵, 譚博學(xué), 高鵬, 等．基于D型行波原理的T接線路故障測距方法［J］. 電力系統(tǒng)保護與控制, 2013, 41(18)：78-82.

　　［2］ 張峰,，梁軍,，杜濤，等．T 型線路的行波精確故障測距新方法［J］．高電壓技術(shù),，2009,，35(3)：527-532．

　　［3］ 郭亮, 呂飛鵬. T型線路的行波測距原理與算法［J］．電力系統(tǒng)保護與控制, 2010, 38(23):6467, 74.

　?。?］ 張永健, 胥杰, 孫嘉. 基于靜態(tài)小波變換的T型輸電線路行波測距方法［J］. 電網(wǎng)技術(shù),2012, 36(6)：84-88．

　?。?］ PINNEGAR C R, MANSINHA L. A method of timetime analysis: the TTtransform［J］. Digital Signal Processing, 2003, 13(4): 588-603.

　　［6］ STOCKWELL R G, MANSINHA L, LOWE R P. Location of the complex spectrum: the S transform［J］. IEEE Transactions on Signal Processing,1996,，44(4):998-1001.