歐訓(xùn)勇

　　（海南熱帶海洋學(xué)院 電子通信工程學(xué)院,， 海南 三亞 572022）

       摘要：首先介紹孤立波的KdV方程,，繼而討論了孤立波SPH方法的數(shù)值求解過(guò)程，選擇SPH光滑核函數(shù)作為正則化高斯核函數(shù),。分析了數(shù)值求解過(guò)程的時(shí)間積分方法,，給出了具體計(jì)算公式，最后給出相應(yīng)程序中的具體參數(shù)下孤立波運(yùn)動(dòng)模擬效果,。

　　關(guān)鍵詞：孤立波,；自由表面流體；SPH

　　中圖分類(lèi)號(hào)：TP311.1文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674 7720.2016.20.019

　　引用格式：歐訓(xùn)勇. 應(yīng)用SPH方法實(shí)現(xiàn)海面孤立波運(yùn)動(dòng)的模擬［J］.微型機(jī)與應(yīng)用,，2016,35（20）：69 71,，74.

0引言

　　孤立波是1834年由RUSSELL S觀察發(fā)現(xiàn)到的，而Korteweg和de Vies于1895第一次通過(guò)理論模型對(duì)孤立波進(jìn)行了解釋?zhuān)环Q(chēng)為KdV理論,。該理論基于弱色散淺水波理論,，淺水波色散由非線(xiàn)性效果平衡，使得波在傳播過(guò)程中在任意距離都保持著一定的振幅和形狀,。KdV方程的精確解描述了孤立子的形狀和傳播速度,。盡管KdV理論被認(rèn)為是一階近似解，很好地描述了真正的孤立波，而高階近似解也一樣可以構(gòu)成,。參考文獻(xiàn)［1］中介紹了任意高階迭代,，逐次逼近模型，在第一次迭代步驟中再現(xiàn)了KdV理論,，然而,，更高階求解需要數(shù)值方法。

　　光滑粒子流體動(dòng)力學(xué)（以下簡(jiǎn)稱(chēng)SPH）是一種無(wú)網(wǎng)格拉格朗日型數(shù)值方法,，由LUCY L于1977年提出,。該方法最初應(yīng)用于天體物理學(xué)領(lǐng)域，然而受海岸工程問(wèn)題所驅(qū)動(dòng),，由MONAGHAN J J在1994第一次提出用于模擬流體流動(dòng),。

　　在過(guò)去的二十多年中，由于在模擬流體自由表面流動(dòng)有突出的性能,，SPH方法成為工程應(yīng)用領(lǐng)域最流行的粒子數(shù)值方法,，例如近海波模擬、海嘯,。本文討論利用SPH方法實(shí)現(xiàn)海面孤立波運(yùn)動(dòng)的三維模擬效果,。

1孤立波的方程

　　孤立波傳播的零階近似解可以用線(xiàn)性波方程描述，而淺水中的波速由以下式子給出：

　　式中,，g為重力加速度,，H為水域的深度。式（1）給出了孤立波傳播的一個(gè)粗略近似值,，而忽略一些特殊的性能，如波的實(shí)際振幅和寬度,，孤立波傳播過(guò)程如圖1所示,。圖1中A為波幅，η(x)是自由表面波形狀函數(shù),。式（1）僅當(dāng)A<<H時(shí)才成立,。

　　線(xiàn)性波的傳播方程是沒(méi)有孤立波解的。KdV方程如下：

　　

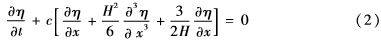
　　式（2）適用于以不同幾何結(jié)構(gòu)構(gòu)造自由表面孤立子的形狀,。函數(shù)η(x,t)表示給定位置x的表面高度,，是一個(gè)與時(shí)間有關(guān)的函數(shù)。單個(gè)自由表面孤立波的KdV方程的精確解由波的形狀函數(shù)給出,，如下：

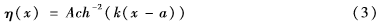
　　式中,，A是振幅，a是孤立子水平偏移量,，k為有效的波數(shù),，其取值如下：

　　一階孤立波的傳播速度計(jì)算公式為：

　　二階孤立波的傳播速度由HAL′ASZ G B做了修正［2］，其公式如下：

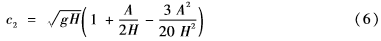
2流體控制方程

　　在流體力學(xué)中，廣泛應(yīng)用歐拉方程和連續(xù)方程來(lái)描述流體運(yùn)動(dòng),。描述流體運(yùn)動(dòng)的偏微分方程中,，局部和對(duì)流通量都包含在拉格朗日微分方程中，如下式：

　　其中,，Φ表示一個(gè)任意的標(biāo)量或矢量場(chǎng),。利用上式的微分算子可以得到無(wú)粘性流體力學(xué)方程如下：

　　式（8）中的v、ρ,、P,、v、g分別指流體的速度,、密度,、壓力、運(yùn)動(dòng)粘度和重力加速度,。在弱可壓縮流體中式(9)被定義為流體密度和壓力之間的關(guān)系：

　　盡管上述各類(lèi)方程包括偏微分方程,、波傳播方程等有解析解，但是通常情況下仍不能得證通過(guò)恰當(dāng)?shù)臄?shù)值方法得到精確解,，只能得到某種程度上的近似解,。然而，這些近似方法經(jīng)常取得不利的數(shù)值特性,，因此它們的一般性,、魯棒性、實(shí)用性都受限制,?？紤]層流的無(wú)粘性，現(xiàn)今的動(dòng)力流體建模都盡量避免對(duì)復(fù)雜湍流模型建模,。

3孤立波的SPH數(shù)值模擬

　　3.1SPH方程

　　無(wú)網(wǎng)格拉格朗日數(shù)值方法稱(chēng)為光滑粒子流體動(dòng)力學(xué)是一種適用于解決式（8）方程系統(tǒng)的工具,。SPH近似數(shù)值方法是基于流體節(jié)點(diǎn)，該節(jié)點(diǎn)稱(chēng)為粒子,，它們?cè)诳臻g中運(yùn)動(dòng)時(shí),，每個(gè)粒子都攜帶有相應(yīng)的物理量，如質(zhì)量,、密度,、壓力、速度等,。這種離散方法是基于受域加權(quán)插值的,，在一個(gè)給定的點(diǎn)，使用臨近區(qū)域內(nèi)的粒子,，這些粒子受一個(gè)稱(chēng)為光滑核函數(shù)W(ri-rj,h)的控制,，形成一個(gè)離散卷積。其函數(shù)如下：

　　式中，i指當(dāng)前粒子,，j是鄰域內(nèi)的一個(gè)粒子,，fi=f(ri)是任意流場(chǎng)中粒子i的位置ri，核函數(shù)Wij=W(ri-rj,，h)帶有緊支性或無(wú)限影響半徑,，h稱(chēng)為光滑長(zhǎng)度，Vj是指定粒子j的物理量值,，N是核函數(shù)Wij影響范圍內(nèi)的粒子數(shù),。公式（10）以離散化構(gòu)造一個(gè)任意流場(chǎng)，流場(chǎng)以粒子散布在空間里,。文中討論的計(jì)算過(guò)程即正則化高斯核函數(shù)［3］,，公式如下：

　　式（11）為改進(jìn)的高斯核函數(shù)。式中r=|ri-rj|,。常量C0和C1由下式計(jì)算：

　　本文討論中,，影響域δ取值為3h。相應(yīng)地,，兩個(gè)一階微分算子梯度和旋度如下：

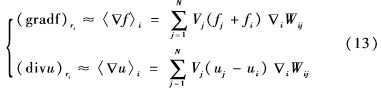
　　在SPH數(shù)值方法中通過(guò)插入數(shù)值擴(kuò)散項(xiàng)到連續(xù)運(yùn)動(dòng)的方程中以保持?jǐn)?shù)值穩(wěn)定性是一種較流行的實(shí)踐方法,。由于自由表面孤立子受慣性力驅(qū)動(dòng)，表現(xiàn)出粘性行為,，動(dòng)量擴(kuò)散（物理數(shù)值）在目前的工作中可以忽略,。相反，在連續(xù)方程中密度的數(shù)值擴(kuò)散項(xiàng)是由文獻(xiàn)［3］算出來(lái)的,，在參考文獻(xiàn)［4］中得以改善,。參考文獻(xiàn)［4］中ANTUONO M提出的基于線(xiàn)性穩(wěn)定分析，密度擴(kuò)散項(xiàng)成為一個(gè)高效的數(shù)值阻尼振蕩工具,。

　　可壓縮性作為另一種特殊的SPH數(shù)值屬性,，可受控于近似弱可壓縮流體方程，這種狀態(tài)假設(shè)一個(gè)正壓流體的壓力和密度之間的線(xiàn)性關(guān)系,。本文使用的SPH數(shù)值方法的離散動(dòng)力學(xué)方程如下：

　　式（14）中，ρ0是參考密度值,，f是外力之和(包括重力),，cs是聲波傳播速度。第一公式右邊第二項(xiàng)是人工密度擴(kuò)散項(xiàng),，在建模中常稱(chēng)為δ SPH,，經(jīng)驗(yàn)系數(shù)ξ=0.1。Ψij項(xiàng)的計(jì)算公式如下：

　　式（15）中右邊第二項(xiàng)帶有正則化密度梯度確保流體質(zhì)量守恒,包括自由表面邊界,，它通過(guò)下式計(jì)算：

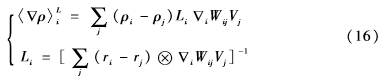
　　式（16）中表示張量積,。正則張量L在流體邊界影響著離散拉普拉斯收斂，它以修正由內(nèi)核截?cái)嘁鸬碾x散梯度人工數(shù)值達(dá)到收斂目的。

　　要降低計(jì)算量,，弱可壓縮流體模型通常運(yùn)行在聲速范圍,，但是其量要足夠大，以保持在預(yù)定義范圍,、獨(dú)立慣性和聲波內(nèi)有足夠大的絕對(duì)密度偏差,。通常取值較現(xiàn)在經(jīng)典流體速度幅值的10倍大，其計(jì)算公式和式（1）相差10倍,，具體如下：

　　式(17)中M取值為10,。

　　利用SPH方法實(shí)現(xiàn)孤立波運(yùn)動(dòng)的模擬效果，整個(gè)實(shí)現(xiàn)過(guò)程涉及求解孤立波SPH數(shù)值解,，確定SPH的邊界及初始條件,，以及孤立波運(yùn)動(dòng)的時(shí)間積分過(guò)程。

　　3.2SPH方法的邊界和初始條件

　　SPH方法的顯著效益（至少在流體建模中）是把任意自由曲面當(dāng)作自然邊界處理而不需要任何額外的計(jì)算負(fù)擔(dān),。另外,，如果流體簡(jiǎn)單地連接著空氣，完全可以從計(jì)算域中忽略,，因?yàn)槭呛銐汉退芏攘?。注意，在?fù)雜流動(dòng)情況下,，如破浪,，空氣可能起著重要作用，因此它不應(yīng)該被忽視,。本文中應(yīng)用兩種SPH不同的邊界條件：一種是邊界墻體和底部,，另一種是周期性的邊界，允許在無(wú)限領(lǐng)域執(zhí)行更一般的計(jì)算［5-6］,。

　　這里的周期邊界的基本量是在翼展方向形成的2D寬域展向近似平面,，帶有三維求解。在SPH的固體邊界的模型中有幾個(gè)基礎(chǔ)性質(zhì)的變種,。

　　3.3SPH方法的時(shí)間步積分

　　式（14）可以通過(guò)任意形式求解,，是穩(wěn)定的數(shù)值解析方法。本文研究應(yīng)用二階預(yù)修正方法,，第一步粒子按△t/2,，具體計(jì)算公式如下：

　　在中間狀態(tài)，密度導(dǎo)數(shù),、壓力,、外力、粒子內(nèi)力（加速度）進(jìn)行近似估算,。使用新的數(shù)值以全步時(shí)間長(zhǎng)度推進(jìn)粒子運(yùn)動(dòng),，其計(jì)算公式如下：

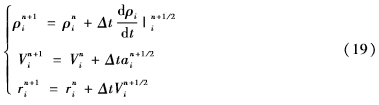
　　為了降低計(jì)算性能的要求,，保持?jǐn)?shù)值穩(wěn)定，時(shí)間步長(zhǎng)可以在每幀中自適應(yīng)選擇,。在當(dāng)前的SPH模型使用CFL條件執(zhí)行計(jì)算,。

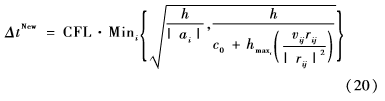
　　上式中，CFL=0.2,，Vij=Vi-Vj

4程序運(yùn)行結(jié)果

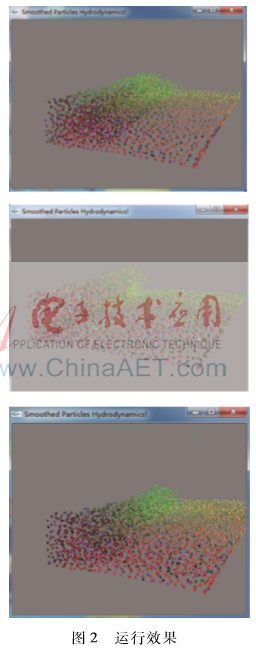
　　根據(jù)以上各節(jié)介紹的方程及數(shù)值求解的過(guò)程,，利用OpenGL三維圖形庫(kù)，在C-free 5環(huán)境下,，使用C++面向?qū)ο蟮木幊谭椒▽?shí)現(xiàn)了對(duì)在淺水灘運(yùn)動(dòng)的孤立波模擬,。由于考慮計(jì)算量，SPH程序使用粒子總數(shù)為4 096個(gè),，即為4K,。粒子質(zhì)量為0.000 205 43，密度為600,，光滑長(zhǎng)度為0.01,，粒子半徑0.004，粒子影響間距為0.005 9,，流體黏度系數(shù)為0.2,。程序運(yùn)行效果截圖如圖2所示。

5結(jié)論

　　程序運(yùn)行環(huán)境為：Intel(R) Core(TM) i32348M @ 2.30 GHz CPU,，4 GB內(nèi)存,，模擬的海浪孤立波運(yùn)行效果非常流暢。以上方法實(shí)現(xiàn)的算法中SPH粒子數(shù)量可達(dá)8 000個(gè)以上,。超過(guò)8 000個(gè)粒子后,，可看到模擬動(dòng)畫(huà)效果出現(xiàn)卡頓了。要想達(dá)到更大的粒子數(shù)量,，采用GPU方法能取得更佳效果,。本研究在應(yīng)用于構(gòu)建模擬大水域海浪運(yùn)動(dòng)，將繼續(xù)深入探索GPU方法及網(wǎng)絡(luò)分塊協(xié)同渲染描繪更大水域波浪運(yùn)動(dòng),。研究成果將應(yīng)用于構(gòu)建光滑粒子流體動(dòng)力學(xué)方法下的船舶運(yùn)動(dòng)的虛擬仿真系統(tǒng),。

　　參考文獻(xiàn)

　　［1］ MOLTENI D, COLAGROSSI A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH［J］. Computer Physics Communications,， 2009,，180（6）: 861-872.

　　［2］ HAL′ASZ G B. Higher order corrections for shallow water solitary waves: elementary derivation and experiments［J］. European Journal of Physics,， 2009，30（6）：1311-1323.

　?。?］ ANTUONO M, COLAGROSSI A, MARRONE S, et al. Free surface flows solved by means of SPH schemes with numerical diffusive terms［J］. Ccomputer Physics Communications,2010,，181（3）:532-549.

　?。?］ ANTUONO M, COLAGROSSI A, MARRONE S. Numerical diffusive terms in weakly compressible SPH schemes［J］. Computer Physics Communications， 2012,，183(12):2570-2580.

　?。?］ 劉瑛琦. 基于SPH方法的數(shù)值波浪水槽研究［D］.南京：河海大學(xué)，2006.

    ［6］ 高睿,，任冰,，王國(guó)玉，等. 孤立波淺化過(guò)程的SPH數(shù)值模擬［J］. 水動(dòng)力學(xué)研究與進(jìn)展（A輯）,2010,25(5):620-629.