0 引言

    FFT（Fast Fourier Transform）是有限長序列DFT（Discrete Fourier Transform）的一種快速算法,，是數(shù)字信號處理中的重要工具。工程實踐中,，根據(jù)數(shù)據(jù)表現(xiàn)形式及中間過程截位規(guī)則不同,，可將FFT處理器分為3種：定點FFT、塊浮點FFT及浮點FFT,。相同的FFT算法,，在3種運算機制下，計算過程中引入舍入誤差不同,，輸出精度存在明顯差異,。經(jīng)研究,，F(xiàn)FT算法舍入誤差與算法分解級數(shù)成正比關系^[1-2]。但舍入誤差的引入與運算過程中的截位規(guī)則,、中間結果范圍緊密相連,，因此有必要探究不同范圍的輸入信號、算法相關參數(shù)與FFT輸出精度的關系,，這對實際工程應用改善輸出精度,、提高噪信比具有重要意義。

1 基4頻域抽取FFT算法

    FFT的核心是利用DFT中旋轉因子的周期性與對稱性,，將長序列DFT逐級分解為短序列的DFT,，從而減少運算量，提高運算速率^[3-5],。常用FFT包括時域抽取FFT與頻域抽取FFT,，現(xiàn)介紹工程中廣泛應用的一種頻域抽取FFT算法，基4頻域抽取算法,。

    長度為N的x(n)序列DFT變換為：

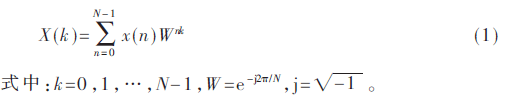
    x(n)按順序均勻分為4個序列：x(i),，x(i+N/4)，x(i+N/2),，x(i+3N/4),。X(k)則按照除以4所得余數(shù)分為4組：X(4r)，X(4r+1),，X(4r+2),，X(4r+3)，i,，r=0,，1，…,，N/4,。則基4頻域抽取一次分解為：

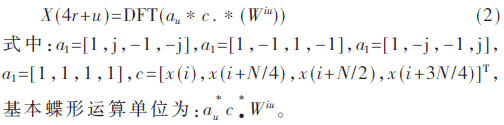
    從式(1)與式(2)對比可以看出,，長度為N的長序列進行一次基4 DIF分解,，N²次復數(shù)乘累加的運算量，降低至N²/4+2N,，且包含±j,，±1，W⁰等因子的單元可進一步簡化運算,。長度為N的序列,，可進行l(wèi)og₄ N次分解，因此FFT算法大大降低離散傅里葉變換運算量,。

2 定點,、塊浮點,、浮點FFT運算過程

    影響FFT輸出精度的因素主要包含：系數(shù)量化誤差，運算過程中舍入誤差,。本文主要探究運算過程中舍入誤差對FFT輸出精度的影響,。不同運算機制，數(shù)據(jù)表現(xiàn)形式及輸出截位規(guī)則有較大差異,，引入舍入誤差不同,，導致最小精度不同。因此有必要對采用定點,、塊浮點,、浮點運算機制時，基4算法運算單元中數(shù)據(jù)表現(xiàn)形式,、輸出截位規(guī)則,、輸出最小精度進行分析。

2.1 定點FFT

    定點FFT是輸入,、旋轉因子,、輸出均為定點形式的一種FFT運算機制。每級蝶形運算,，根據(jù)輸入位寬對運算結果采取高位截取,。如圖1所示，輸入數(shù)據(jù)位寬為a,，旋轉因子位寬為b,。蝶形輸入與因子±j，±1進行乘加運算,，幅值全范圍位寬擴展至a+2位,，與b位有符號旋轉因子相乘位寬擴展至a+b+1位，每級蝶形輸入位寬要求相同,，因此以四舍五入法截取高a位蝶形運算結果進行下級蝶形運算,。

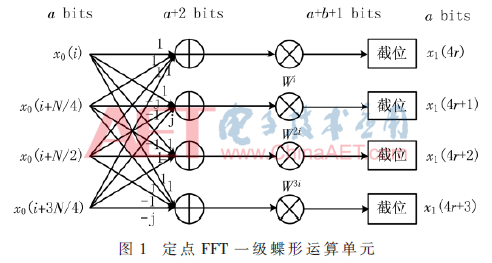
    除去與旋轉因子相乘造成的位擴寬，基4定點FFT每級蝶形運算以全范圍位寬溢出2位為前提進行舍入,。每進行一級蝶形運算,，中間結果最小精度擴大4倍。因此,，輸入序列長度為N時,，輸出FFT最小精度為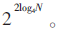定點FFT輸出最小精度只與分解級數(shù)有關。

2.2 塊浮點FFT

    塊浮點FFT與定點FFT區(qū)別在于對中間截位過程的優(yōu)化,，其結果包含頻譜數(shù)據(jù)及指數(shù),。定點FFT默認每級蝶形輸出結果均出現(xiàn)符號位溢出，事實上不同量級的輸入，中間結果符號位溢出情況是不同的,，塊浮點FFT通過監(jiān)測每級蝶形運算輸出范圍決定截位,，從而減少被截取位寬，降低了舍入誤差,。如圖2所示,，以正負最大的數(shù)值為標準，對每級蝶形輸出結果進行截位處理,。

    塊浮點FFT通過指數(shù)表征總體移位結果,，輸出指數(shù)為exp，則最小精度為2^exp,，指數(shù)由算法輸入位寬,、輸入信號、運算級數(shù)共同決定,。因此塊浮點最小精度與算法輸入位寬,、信號幅值范圍、運算級數(shù)相關,。

2.3 浮點FFT

    IEEE754標準是1985年IEEE（Institute of Electrical and electronics Engineers,，電子電氣工程師協(xié)會）提出的浮點運算規(guī)范，為浮點運算部件工業(yè)標準^[6],。IEEE754浮點格式如下：

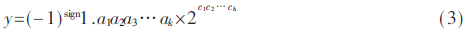
    如式(3)所示,，IEEE754浮點格式包含一位符號位，h位無符號偏置指數(shù),，k位尾數(shù),。數(shù)據(jù)進行二進制科學計數(shù)法表示后，指數(shù)部分加上偏置值作為偏置指數(shù),，小數(shù)部分依次截取k位有效數(shù)字作為尾數(shù),。如表1所示，IEEE754共提供3種位寬的基礎二進制浮點格式,。

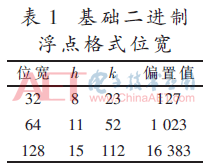
    相同位寬下,，浮點格式所表示的數(shù)據(jù)范圍比定點格式大得多。尾數(shù)最低位權值為所能表示的最小精度,，因此數(shù)據(jù)越大,，浮點表示精度越低。

    浮點FFT輸入,、輸出,、旋轉因子均為浮點表示形式,，涉及的運算均遵循浮點運算準則,。計算結果有效位寬溢出導致的舍入誤差是浮點FFT主要誤差來源。

3 噪信比分析

    為進一步對不同運算機制下FFT計算精度問題進行探索，我們使用輸出噪信比表征FFT算法相對誤差,，研究運算級數(shù),、算法輸入位寬與輸入信號范圍與FFT精度的關系。

3.1 浮點FFT噪信比

    浮點FFT誤差分析相對困難,，文獻[1]中提出了基2浮點FFT靜態(tài)模型,，輸入為白噪聲時，結果如公式(4)所示,，噪聲與信號均方差比值正比于FFT運算級數(shù)v,。文獻[2]則分析了DIF與DIT以及不同基數(shù)下FFT運算下的舍入誤差。結果表明,，浮點FFT輸出噪信比正比于運算級數(shù),。

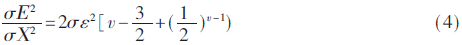
3.2 定點FFT與塊浮點FFT仿真模型

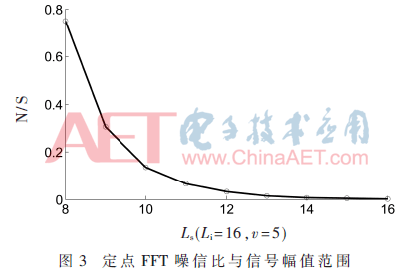
    現(xiàn)于MATLAB平臺建立定點與塊浮點FFT模型。該模型采用基4頻譜抽取算法,，輸入信號范圍,、輸入位寬與旋轉因子位寬可調(diào)。計算噪信比N/S=|x_m-x_mat|/|x_mat|,，x_m為模型輸出,，x_mat為MATLAB平臺64位浮點計算值。通過仿真,，得出輸入為隨機序列時,，輸出噪信比與信號全范圍位寬Ls、FFT輸入位寬Li,、運算級數(shù)v的關系,。

3.2.1 噪信比與輸入信號幅值范圍關系

    從圖3與圖4可以看出，定點FFT噪信比隨輸入信號范圍增大而下降,。但對于塊浮點FFT,，輸入信號范圍接近輸入位寬時，噪信比停止下降,，甚至會略有上升,。運算級數(shù)固定，定點FFT輸出最小精度不變,。頻譜分量大于最小精度時,，增大信號輸入范圍，能夠增大頻譜分量,，有效減小頻譜失真率,，降低輸出噪信比。而塊浮點FFT最小精度是隨信號頻譜分量范圍變化的,，信號輸入范圍較小時,，塊浮點FFT最小精度不變，呈現(xiàn)與定點FFT相同的規(guī)律，但隨著信號范圍增大,，最小精度也隨著變化,，因此噪信比不呈現(xiàn)下降的趨勢。

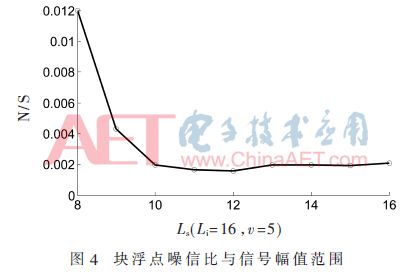
3.2.2 噪信比與輸入序列長度關系

    從圖5與圖6可以看出,，無論是定點FFT與塊浮點FFT,，噪信比都與運算級數(shù)近似正比。這是隨著運算級數(shù)增加,，舍入誤差線性累積的結果,。

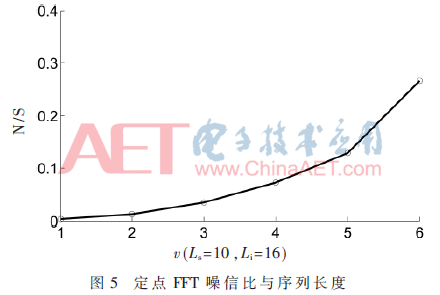
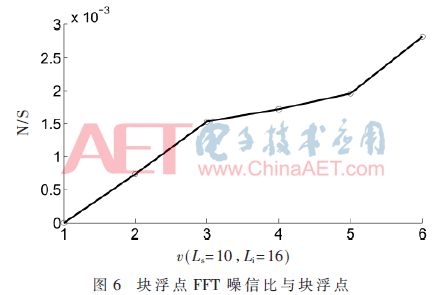
3.2.3 噪信比與FFT輸入位寬關系

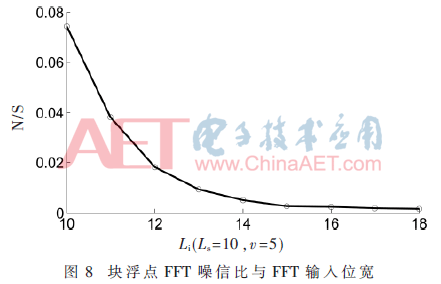
    從圖7與圖8可以看出，定點FFT輸出噪信比與定點FFT輸入位寬無關,，而塊浮點FFT噪信比隨著輸入位寬增大而減小,。這是因為定點FFT，輸入位寬并不影響最小精度,。而對于塊浮點運算機制,，F(xiàn)FT輸入位寬的增加，降低輸出最小精度,，輸出噪信比降低,。

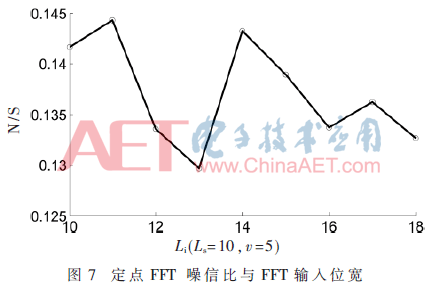
4 小信號FFT精度問題

    實際工程中，使用FPGA進行頻譜計算,，當輸入為白噪聲信號時,，出現(xiàn)頻譜失真的情況，經(jīng)分析頻譜失真與塊浮點FFT計算精度有關,。

    工程中,，對射頻接收機輸出信號進行采樣，經(jīng)過DDC,，不同濾波帶寬濾波抽取后,，使用塊浮點FFT ip核進行FFT計算，F(xiàn)FT輸出結果進行位擴展后,，依照式(5)進行幅值計算,。

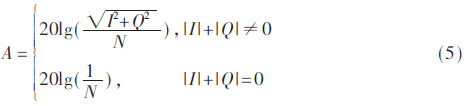
    幅值計算包含對數(shù)運算，因此在位擴展之后,，將FFT ip核輸出實部虛部分量都為0的點幅值固定為常值1,，是幅值計算過程基于最小值的數(shù)值優(yōu)化。

    當輸入為白噪聲情況下,，降低信號帶寬,，出現(xiàn)了圖9所示的信號頻譜失真。

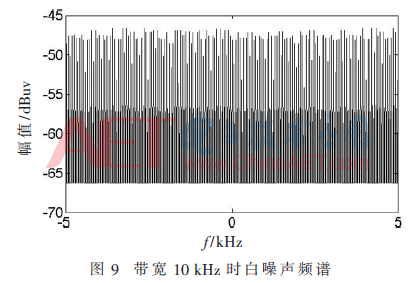
    當濾波帶寬較小時,，頻譜能量小,，輸出頻譜分量小于FFT ip核輸出最小精度,，因此出現(xiàn)較多零點。

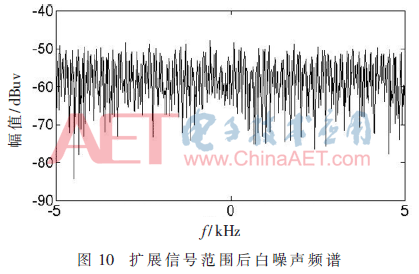
    根據(jù)圖4所示規(guī)律,，塊浮點FFT運算，當信號范圍較小時,，噪信比隨著輸入范圍增大而減小,。因此可通過擴大輸入信號范圍來減小噪信比，統(tǒng)一將信號時域分量擴大一定比例值,，以使頻譜分量大于ip核輸出最小精度,，減小頻譜失真，后續(xù)計算環(huán)節(jié)將比例值抵消后得到新的頻譜如圖10所示,，頻譜失真現(xiàn)象得到改善,，驗證了仿真結論的正確性。

5 結論

    本文通過分析定點,、塊浮點,、浮點機制下，基4算法基本單元運算數(shù)據(jù)表現(xiàn)形式及截位規(guī)則,，得出不同運算機制下,，F(xiàn)FT舍入誤差及輸出最小精度。利用仿真模型,，得出定點,、塊浮點FFT噪信比隨輸入信號范圍、FFT輸入位寬,、序列長度的變化趨勢,，并基于仿真結論，解決了實際工程中會遇到的小信號頻譜失真問題,，驗證了仿真結果的正確性,，對工程師在實際工作中有很強的借鑒性和參考價值。

參考文獻

[1] WEINSTEIN C.Roundoff noise in floating point fast Fourier transform computation[J].IEEE Transactions on Audio and Electroacoustics,，1969,，17(3)：209-215.

[2] THONG T，LIU B.Accumulation of roundoff errors in floating point FFT[J].IEEE Transactions on Circuits and Systems,，1977,，24(3)：132-143.

[3] COOLEY J W，TUKEY J W.An algorithm for the machine calculation of complex Fourier series[J].Mathematics of computation,，1965,，19(90)：297-301.

[4] COCHRAN W T，COOLEY J W,，F(xiàn)AVIN D L,，et al.What is the fast Fourier transform?[J].Proceedings of the IEEE,，1967，55(10)：1664-1674.

[5] BRIGHAM E O,，BRIGHAM E O.The fast Fourier transform[M].Englewood Cliffs,，NJ：Prentice-Hall，1974.

[6] Floating-Point Working Group.IEEE standard for binary floating-point arithmetic[C].SIGPLAN.1987,，22：9-25.